27 of 100: Area Intersection Enigma
The dots in the grid above are all equally spaced. In square units, what is the area of the region shaded orange?
There are many ways to solve this − one of which involves finding the "coordinates" of that intersection point.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
Very elegant.
good drawing u hit it
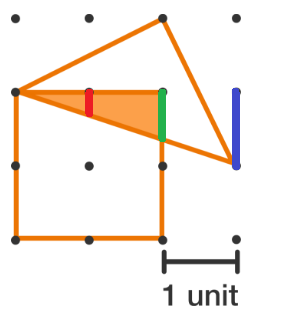 In the diagram the blue line is 1 unit, so the red line is
3
1
and the green line is
3
2
In the diagram the blue line is 1 unit, so the red line is
3
1
and the green line is
3
2
Here is the triangle we are interested in:
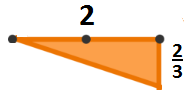 The area is therefore
2
1
×
2
×
3
2
The area is therefore
2
1
×
2
×
3
2
This equals 3 2
Nice and simple! Just the way I did it.
@Delight Dall'Olio Red and green lengths can be deduced from similar triangles. (the 3 triangles with the red, green, blue bases and top vertex at (2, 1) are similar)
Log in to reply
i actually know that but you should add it to the solution so it won't be incomplete
how do you know green and red line measure, u can't just assume that without algebra, just by looking to the simetry.
Log in to reply
The diagonal line that intersects the r e d , g r e e n , and b l u e lines in this solution has an X : Y ratio of 3 : 1 .

All of the sub-triangles have the same proportions.
The p i n k base of the r e d triangle is 1 , so the length of the r e d side must be 3 1 to maintain the same proportions.
The p i n k base of the g r e e n triangle is 2 , so the length of the g r e e n side must be 3 2 to maintain the same proportions.
Let's treat the grid as the Cartesian coordinate plane with the bottom left dot representing the origin. The side of the triangle intersecting the square can be represented by the line y = − 3 1 x + 2 . The intersection point between ( 2 , 1 ) and ( 2 , 2 ) is simply the point on the line when x = 2 :
f ( 2 ) = − 3 1 ⋅ 2 + 2 = 3 4
The base of the shaded triangle is the distance between ( 2 , 3 4 ) and ( 2 , 2 ) , which is 3 2 .
Now we can solve for the area of the shaded triangle:
A = 2 1 b h = 2 1 ⋅ 3 2 ⋅ 2 = 3 2
I did the same till finding the equation of the straight line, then used integration to find the area( to make it more complex ;P) . Your method of finding area is much better!
A simple solution for those familiar with integration.
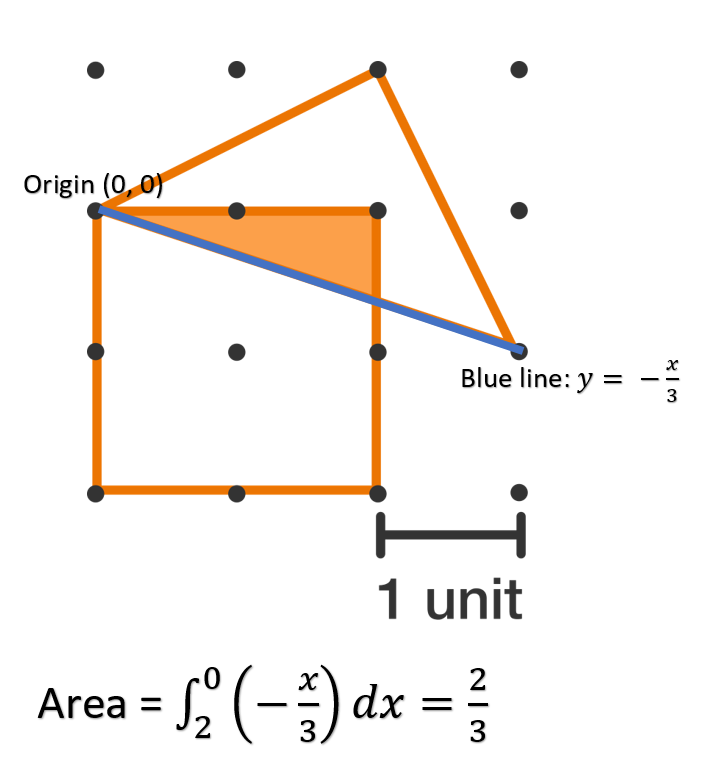
I believe that 2 should be on top and 0 on the bottom (as defined by Wikipedia: https://en.wikipedia.org/wiki/Integral)
Log in to reply
Since the line is negative for x>0, your integral is also negative and so the bounds are swapped to give a positive result :)
Although there is much easier solution using properties of similar triangles, I will present the solution which Brilliant staff mentioned above, done using some simple analytic geometry which involves finding coordinates of the intersection point. Note that this might be the most efficient approach, if the problem was more difficult and complex.
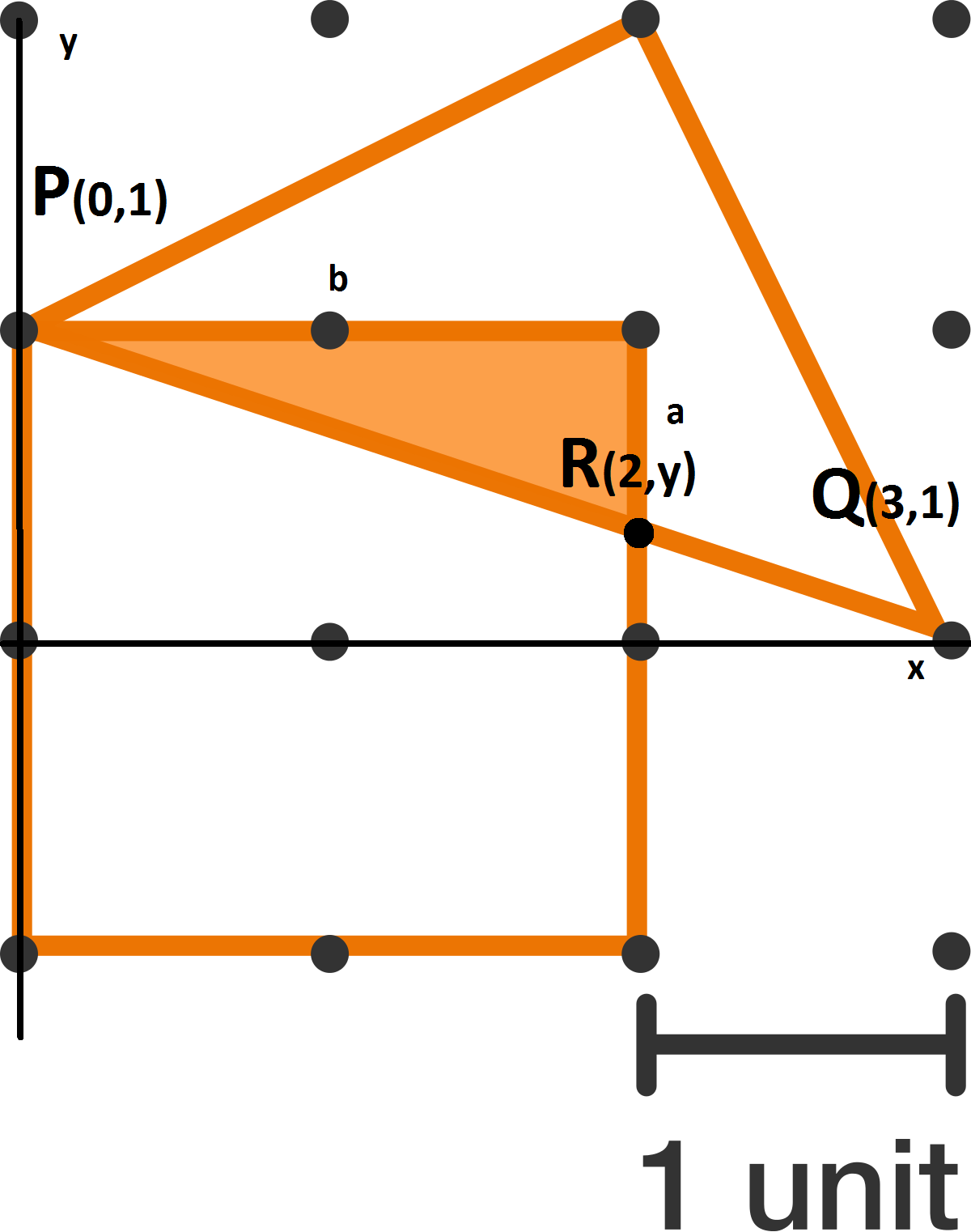
Notice that I added few points and lines to the original picture: I added x and y axis, as well as points P ( 0 , 1 ) ; Q ( 3 , 0 ) ; R ( 2 , y ) . Let us first determine equation for line which goes through P , R and Q , let us call it p . Remember that every line can be expressed in form y = k x + n , where k is slope of the line (tangent of an angle which the line forms with x -axis) and n is value of y when x equals 0 . Since we know coordinates of P and Q , we can set up following system:
1 = k × 0 + n
0 = k × 3 + 1
From the first equation of the system, we get n = 1 . Plugging it in the second one, we get k = − 3 1 . Now, we have general equation for the line p :
y = − 3 1 x + 1
Now we can calculate the y -coordinate of point R just by plugging value of x in our general formula.
y = − 3 1 × 2 + 1
y = 3 1 .
Next, it's obvious that side a of the shaded triangle is equal to: a = 1 − y ⇒ a = 3 2 .
Finally, we've got everything we need to calculate the area of the shaded triangle:
A = 2 a b = 2 3 2 × 2 = 3 2
Use tangent. Calculate tangent. Tangent is 1/3. Calculate side using tangent . Side is 2/3. Calculate area using formula for a right triangle.
In the diagram, the hypotenuse and the smaller base of the orange triangle are shown as extended. Let us take the extension upto next black dot only. These black dots when joined are forming a triangle similar to orange triangle with side lengths equal to half of the sides of orange triangle.
As such, the smaller bases of these two triangles, on a combined length of one unit, stand divided into lengths of 2/3 and 1/3 respectively.
So, the two perpendicular sides of orange triangle are 2 and 2/3, and the area is
= (1/2)(2)(2/3) = 2/3.
The area of the larger right triangle which covers the orange area as a part of it and has legs 1 and 3 is 1/2(3)(1) = 3/2. Let the base of the right orange triangle be r. Then knowing the area of a trapezoid, it is obvious that 3/2 = r + (r + 1)/2. Solving for r = 2/3. Then the area of the orange area which is a right triangle is 1/2(2)(r) = r = 2/3.
The shaded region is similar to a triangle with base 3 and height 1, but its side lengths are 2 / 3 the side lengths of that triangle. Thus the area of the shaded region is ( 2 / 3 ) 2 the area of the larger triangle. The larger triangle's area is ( 1 / 2 ) ∗ 3 ∗ 1 = 3 / 2 so the shaded region's area is ( 3 / 2 ) ∗ ( 2 / 3 ) 2 = ( 3 / 2 ) ∗ ( 4 / 9 ) = 2 / 3 .
I did this by eyeballing this. The slanted line crosses most closely to 2/3 of the way down. I followed from there.
I used basic math since I am 12. Area of triangles: (Base times height)divided by 2
(2 x 2/3) /2
In a square, add the orange.
A relatively easy solution that involves no trigonometry or calculus or anything.
First note that most of the picture and the lines in the picture are mostly irrelevant. The only part that really matters is this part:
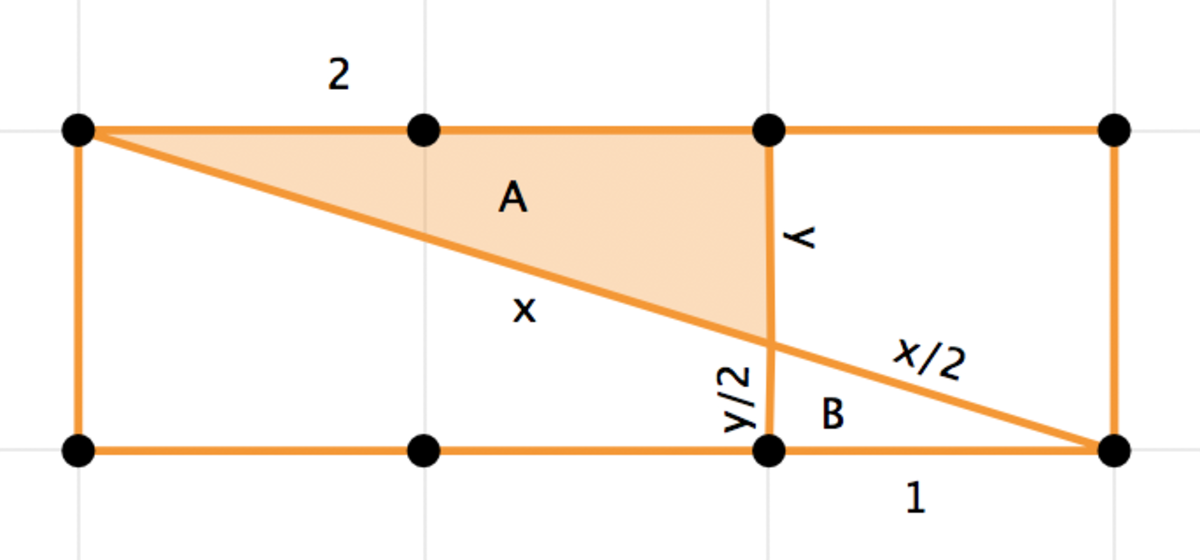
The area of triangle A is what is of interest. Note that triangle's A and B are similar triangles as we can see that they have exactly the same angles. The "base" of triangle B is 1 and the "base" of triangle A is 2 (as labeled in the picture.) Therefore we know that all of the sides of triangle A must be twice as large as triangle B . (As labeled in the picture.)
We can solve for the heights of the triangles: y + 2 y = 1 ⇒ y = 3 2 .
Therefore the area of triangle A is 2 1 × 2 × 3 2 = 3 2 .
LaTeX: The area of the orange square is limited by ( x = 0 ) , y axis and ( x = 2 )
LaTeX: and the straight line ( y = 2 ) and we get an integral
LaTeX: ∫ 0 2 2 d x
LaTeX: As we can see on the graphic, the straight line ( D F )
LaTeX: is composed of two points : F ( 3 ; 1 ) and D ( 0 ; 2 ) .
LaTeX: we have to find the equation of the straight line ( D F ) : y = a x + b
LaTeX: ( 3 a + b = 1 ) and ( 0 a + b = 2 ) ⟺ ( b = 2 ) and ( 3 a + 2 = 1 ) ⟺ ( b = 2 ) and ( a = − 3 1 )
LaTeX: we now have the equation of the straight line ( D F ) : y = − 3 1 x + 2
LaTeX: The area limited by ( x = 0 ) , y axis and ( x = 2 ) and the straight line ( D F ) :
LaTeX: ∫ 0 2 ( − 3 1 x + 2 ) d x
LaTeX: we notice that y = 2 > y = − 3 1 x + 2 , then we just have to substrat the two areas
LaTeX: ∫ 0 2 2 d x − ∫ 0 2 ( − 3 1 x + 2 ) d x
LaTeX: Using linearity, we get : ∫ 0 2 2 − ( − 3 1 x + 2 ) d x = ∫ 0 2 ( 3 1 x ) d x = 3 1 ∫ 0 2 x d x
LaTeX: A primitive of $x$ is : 2 1 x 2 then we get : 3 1 ∫ 0 2 x d x = 3 1 [ 2 1 x 2 ] 0 2 = 6 1 [ x 2 ] 0 2
LaTeX: = 6 1 [ x 2 ] 0 2 = 6 1 ( 2 2 ) = 6 4 = 3 2
LaTeX: Finally, the result is : 3 2
LaTeX: It was easy to find the slope of ( D F ) : y = − 3 1 x + 2
LaTeX: just watching the diagonal on the graphic between D and F
LaTeX: x y = 3 1 the stright line is descending so the coefficient is negative
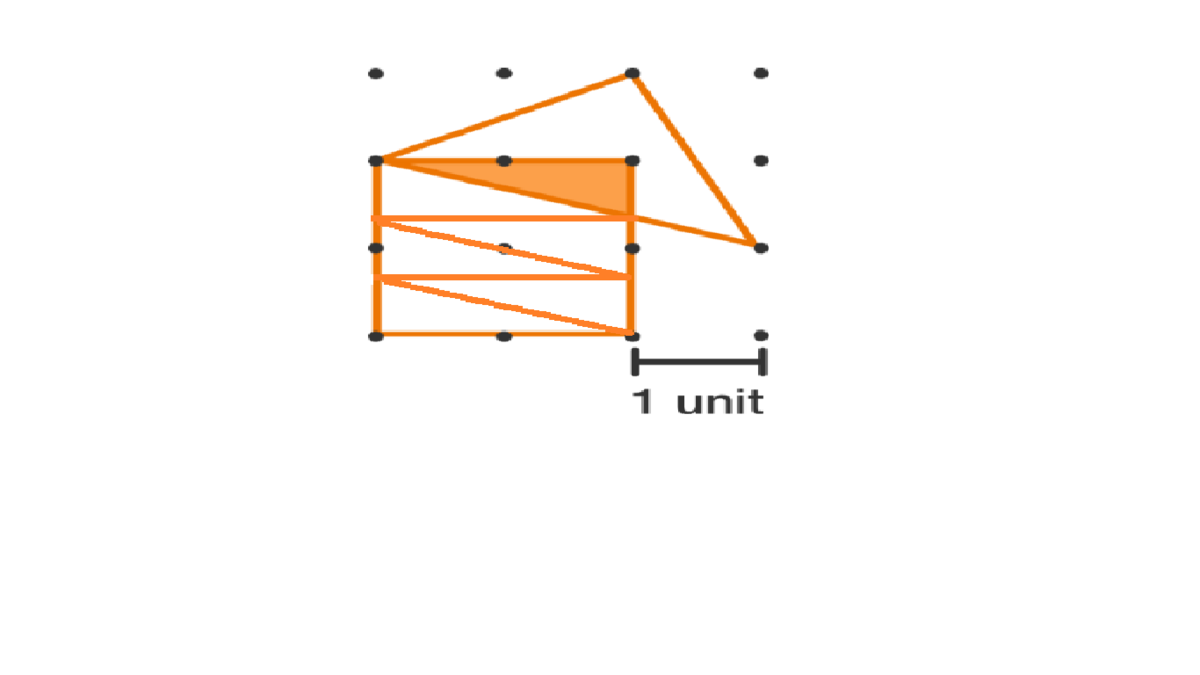
Clearly, we can see that 3 rectangles can be contained in the square. As the side of the square is 1 × 2 = 2 units , the smaller side of the rectangle is 2 ÷ 3 = 3 2 units . Hence, the area of the triangle = 2 1 × 1 2 × 3 2 = 3 2 units .
[Sorry for the picture being bad.]
The bigger triangle is right-angled, and since its smaller side lengths equal 5 , its area is 2.5. Now notice that the right triangle that is similar to the shaded one has sides that are two times shorter, therefore its area is one quarter of the shaded one. If we name the area of the shaded triangle X, we get the following equation:
2 5 = X + 1 + 1 - 4 X
2 1 = 4 3 X
X = 3 2
8 units for the square 7 units for the triangle I added the smaller orange section to the bigger side and it made a rectangle in the 1 unit square. I divided it by the answers so like dividing it by 3rd it made and searching for the closes ratio of that 3rd which was 3 2
extend the orange area out to the next vertical. making a 3x1 triangle area 3/2. notice that the orange area desired is this, scaled down by a factor of 2/3. which means the area is scaled down by a factor of (2/3)^2 or 4/9. 4/9 x 3/2 = 2/3.
Similarity is what most people used, I presume. I did so as well. This is a different similarity, but basically follows the same idea: There are a lot of parallelities and right angles in the diagram, let us look for similar triangles!
It's difficult to write up a solution without having the points labelled. Call the bottom left point A 1 1 , the point right of that A 2 1 , the point above A 1 1 then A 1 2 and so on, so that the top right point is called A 4 4 . Let the X = A 1 3 A 4 2 ∩ A 3 1 A 3 3 . Then △ A 3 3 A 1 3 X ∼ △ A 3 2 A 4 2 X . So ∣ X A 3 2 ∣ ∣ A 3 3 X ∣ = ∣ A 3 2 A 4 2 ∣ ∣ A 1 3 A 3 3 ∣ = 2 , thus ∣ A 3 3 X ∣ = 3 2 , since ∣ A 3 3 A 3 2 ∣ = 1 , and now it is easy to compute the area.
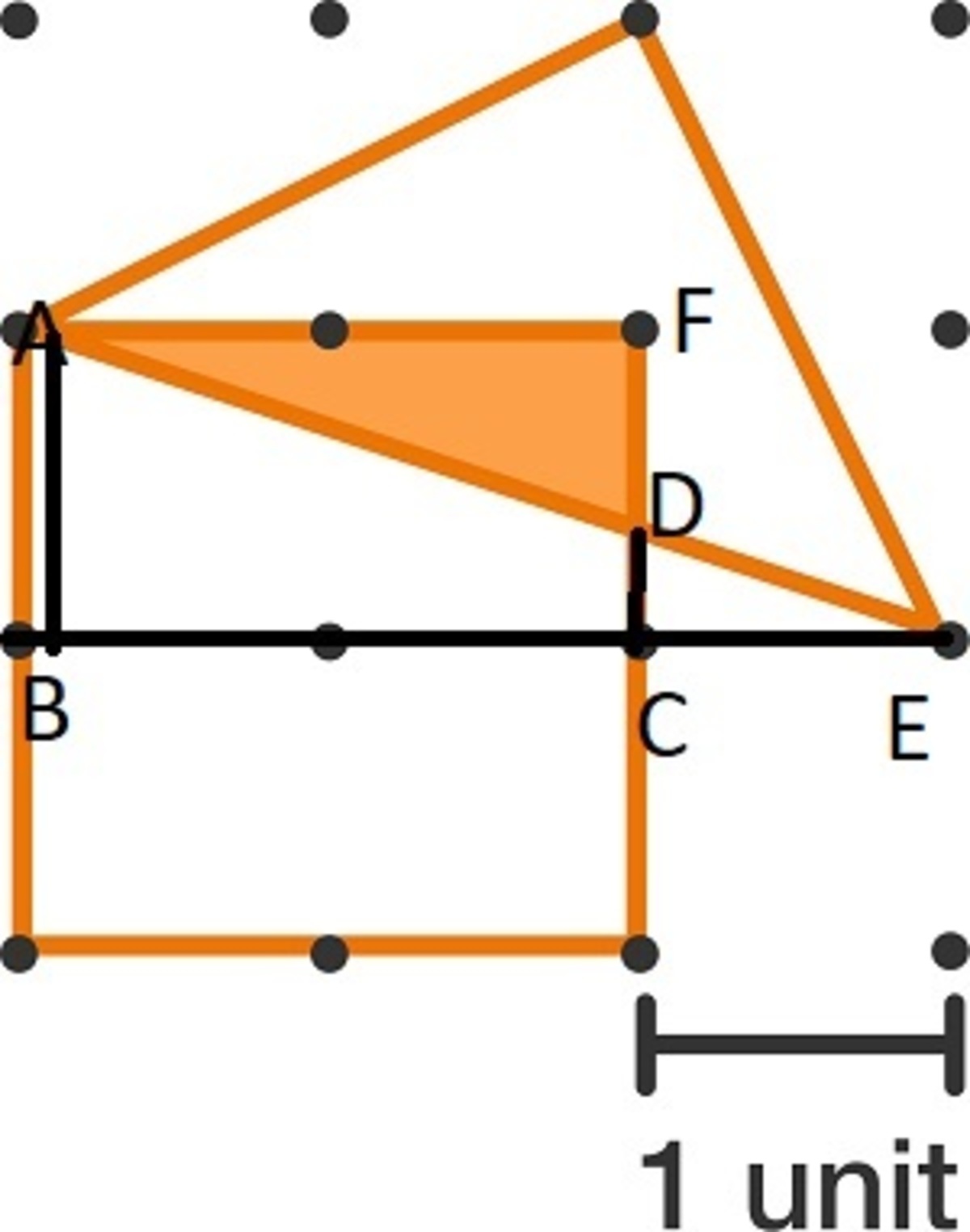
Consider points A, B, C, D,E and F above. We know the ratio of AB to BE is 1:3. So DC to CE has to be 1:3 as well. It follows then that DF=2/3:1. So, since AF=2, we have 2 x 2/3 x 1/2, or 2/3 as the total area for triangle ADF.
Here blue arrowed side is 2/3 unit See the black side in right most is 1 unit. According to similarity of triangle.
So required area is 2/3×2×1/2 =2/3