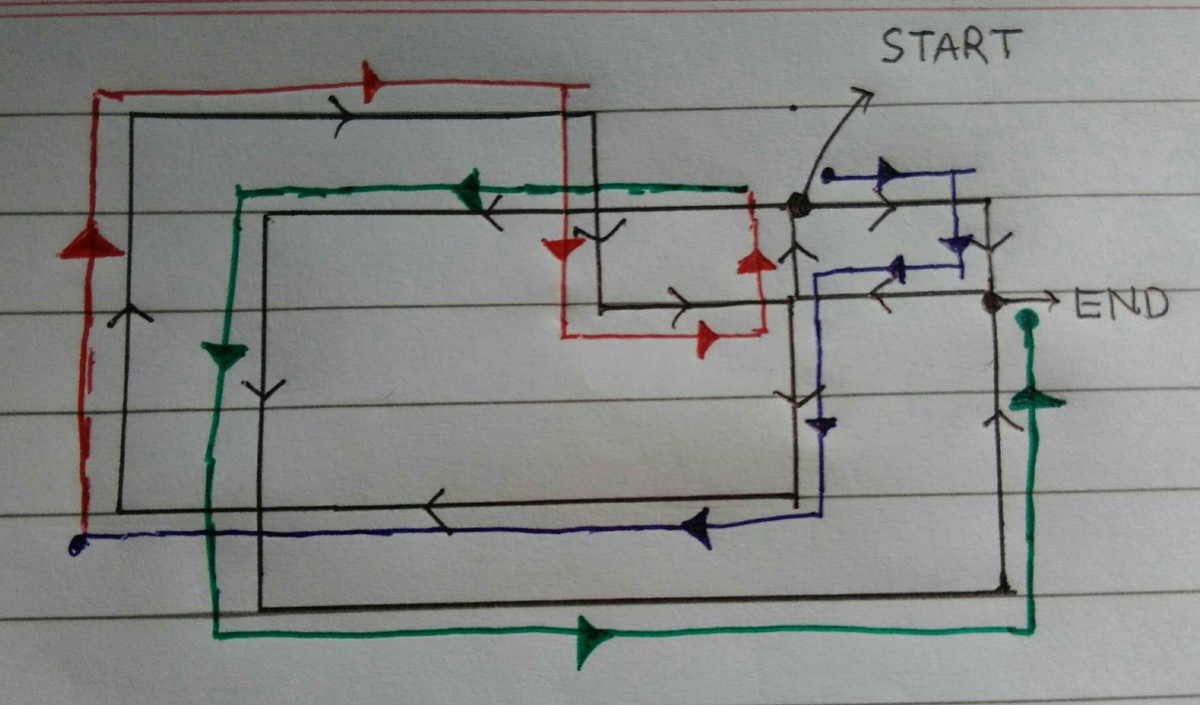
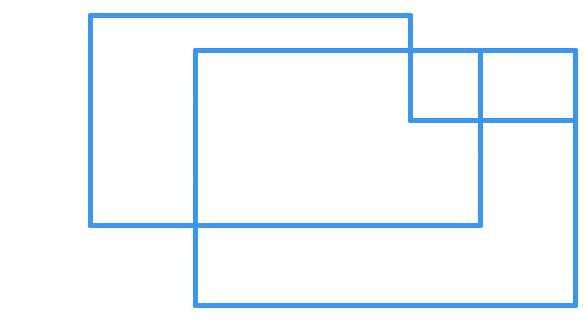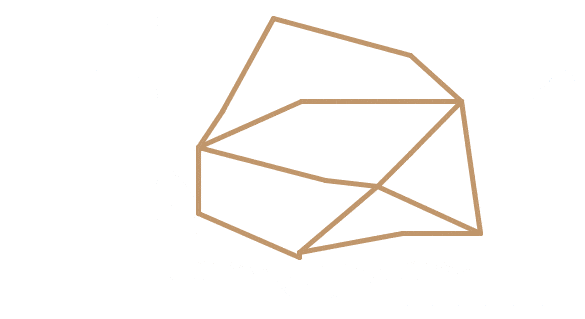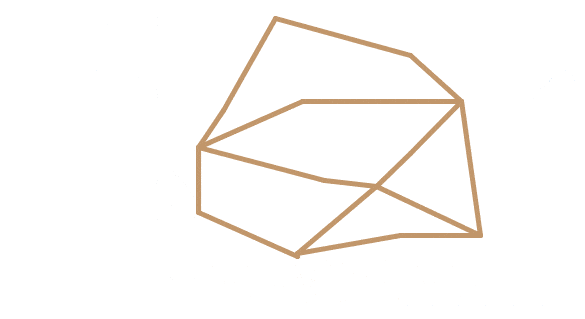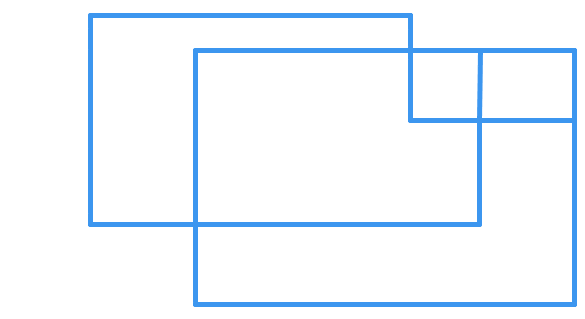
29 of 100: Trace It!
Starting with your pencil at a location of your choice on the two-dimensional figure, is it possible to trace this entire figure without lifting your pencil or redrawing a line? (Crossing at an intersection is ok.)
It might help to simplify the diagram; the important points are the intersections.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Idiot question : there are two points (even) that has number of connection into them are three ( odds). Then they must be start point and end point if there is solution.
The questions stated "Starting with your pencil at ANY point on the figure,". The answer should be NO not YES because there are only two points that you can do this not ANY
Log in to reply
I faced the same problem with the problem statement. By the way, you should report this. Otherwise, it won't be fixed.
Is it "it is?"
The above problem is related to the Eulerian circuit problem in graph theory, that is traversal of a graph without breaks and starting and ending at the same vertex and the related Eulerian Path problem (the problem above is related to the latter) where one can begin and end at different vertices. The former is possible only when all vertices are of even degree and the latter is possible if either 0 or 2 vertices have odd degree. Our diagram above can be simplified to a 5 vertex graph, 3 of degree 4 (where the lines intersect) and 2 of degree 3 where the lines touch the encircling quadrilateral). Since there are 2 and only 2 vertices of odd degree, the figure can be traced completely with the given conditions.
I would say this problem is not only "related to" the Eulerian path problem, but that it
is
the Eulerian path problem. But I guess that would just be arguing about semantics.
One nice thing about the Eulerian path problem is that it can be solved (almost) greedily. You can greedily partition the edge set into paths, and then if you need to, stich together the paths into one long path using common vertices.
Good solution!
https://brilliant.org/wiki/eulerian-path/
excuse me =))) is that called "topo geometry" ?
Log in to reply
If you mean topology, yes, graph theory is a branch of topology
Log in to reply
I suppose you could view graph theory as a branch of topology, but that would really miss a lot of what's going on in the field. Both fields start from set theory but they go in very different directions.
i just find this problem very amazing and want to know more about it . thank you all =)))
I used different colors in the figure only to make it easier to visualize.
Although I am not sure if it is commonly known around the world, I was familiar with a very similar puzzle, only with a different figure to trace. Fortunately, It did not take long to realize that the figure above was actually a deformed version of the one I knew "the house with X".
I think it was my aunt who introduced me to the puzzle, many years ago (perhaps a decade, maybe more). I did not expect it to become useful after all these years, but I had found a few different solutions, all of which work for this one as well. Below is an example:
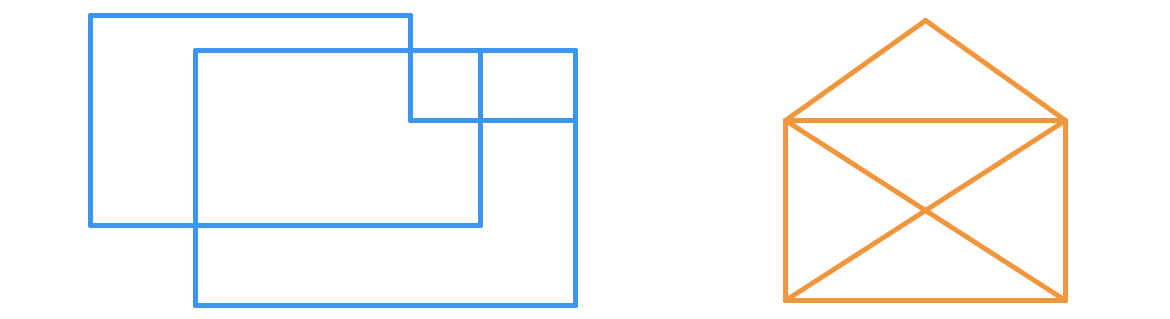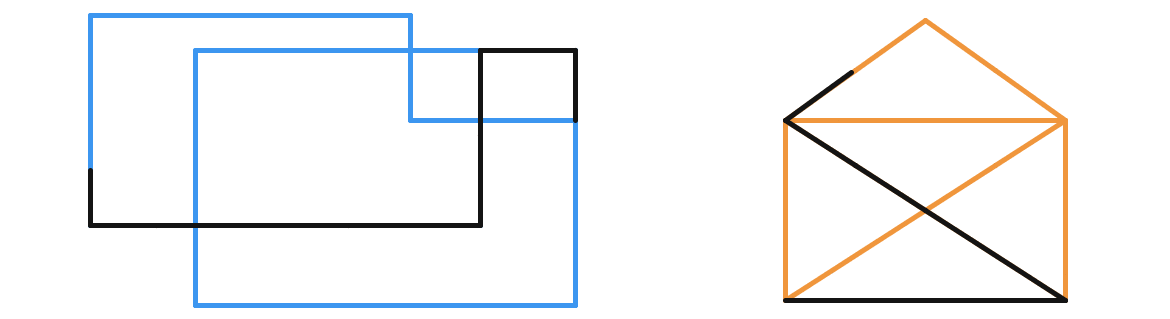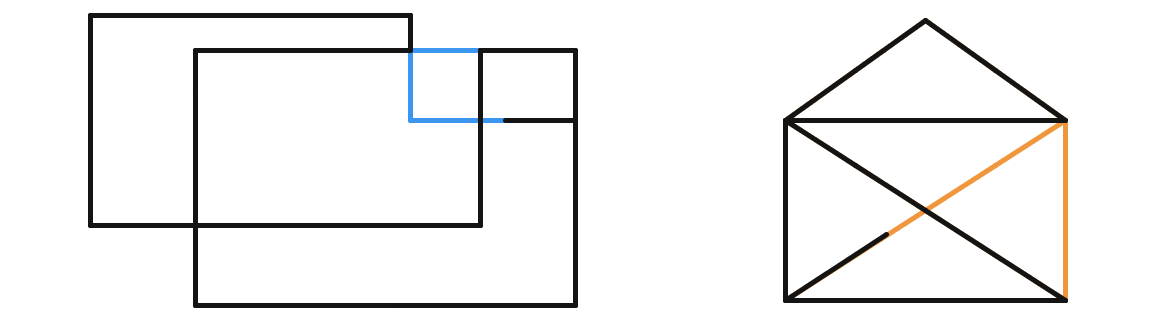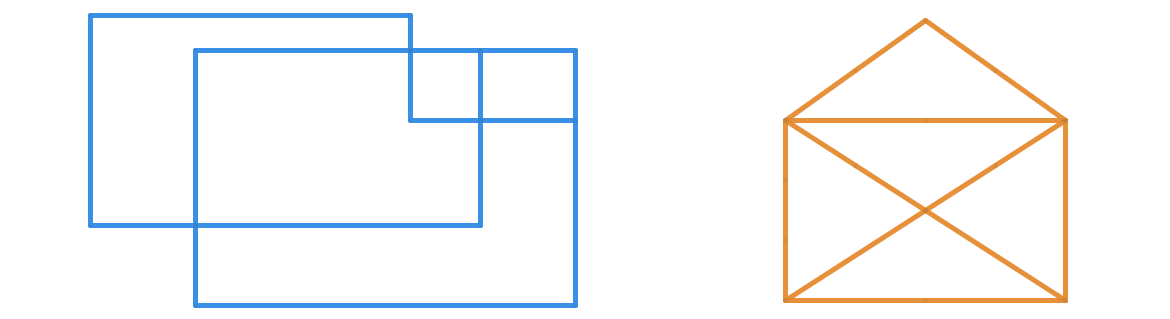
This is probably not a very 'mathematical' approach compared to many of the other solutions given, but I think it comes down to the same thing. I was unknowingly familiar with an example of a Euler Path problem, which was essentially identical to the one above.
+1 for seeing the similarity and producing those cool animations. May I ask how you made them?
inspired solution!
@Andrew Lamoureux @Har Gey - Thank you very much. Not only for the nice comments, but also for finding this and pulling it out from under heaps of other solutions. (The latter part also goes for whoever another person voted up)
I am so grateful, because I thought it would stay unnoticed. The time and effort I put into this wasn't for the sake of upvotes, but I did want people to see it.
@Andrew Lamoureux - In fact, I am happy to share the information.
I used Processing; a programming language with intuitive visual output.
The first one was not so difficult (although tedious). It was quite straightforward to make the base of the second one as well, but it took unexpectedly long to make it look the way I wanted (to give it the correct rhythm{?}).
Thank you for asking.
Here is a possible solution.
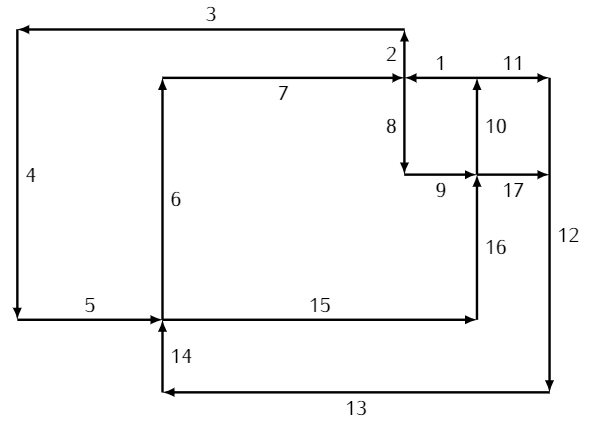
The solution is what's called an Euler Path. If you look at the number of edges that meet at each vertex, you'll notice all vertices but two are the junction of an even number of edges. When there are exactly two vertices with an odd number of edges this means every line can be drawn exactly once, but the path will start and end at different vertices (if all vertices had an even number of edges that's an Euler Circuit- where the path will start and end at the same point); the two odd vertices will be the starting and ending points, and there are multiple paths between those two points.
Thanks, I was wondering if there was a name for this type of problem !
Graph theory :)
Yes, applying Euler's Theorem, a basic result from graph theory. This theorem states that a path over the entire (connected) graph using each edge exactly once,exists when there are two or less vertices of odd order. When all are even the path can start and end at the same vertex, when there are two odd vertices the path must start at one and end at the other.
The example given is a graph with two vertices with odd order and the rest have even order. By Euler's theorem there exists a path, using each edge exactly once, over the entire graph starting at one odd vertex and ending at the other.
That is an Eulerian graph.
Follow the rainbow. It's pretty self-explanatory!
Just look for two intersections that is connected by odd-numbered lines. There must be at most 2 of these. Otherwise, it couldn't be traced entirely.
It is not possible starting from any point. It is possible starting from either one of two points.
*This solution was in response to the previous wording of the question. I don't remember the exact wording, but it was something like:
Starting with your pencil at any point on the two-dimensional figure, is it possible to trace this entire figure without lifting your pencil or redrawing a line? (Crossing at an intersection is ok.)
But since this is clearly a geometry problem and not a logic problem, maybe I shouldn't have been so persnickety.

Actually one of two points, either of the two vertices that have odd order, starting at one and ending at the other.
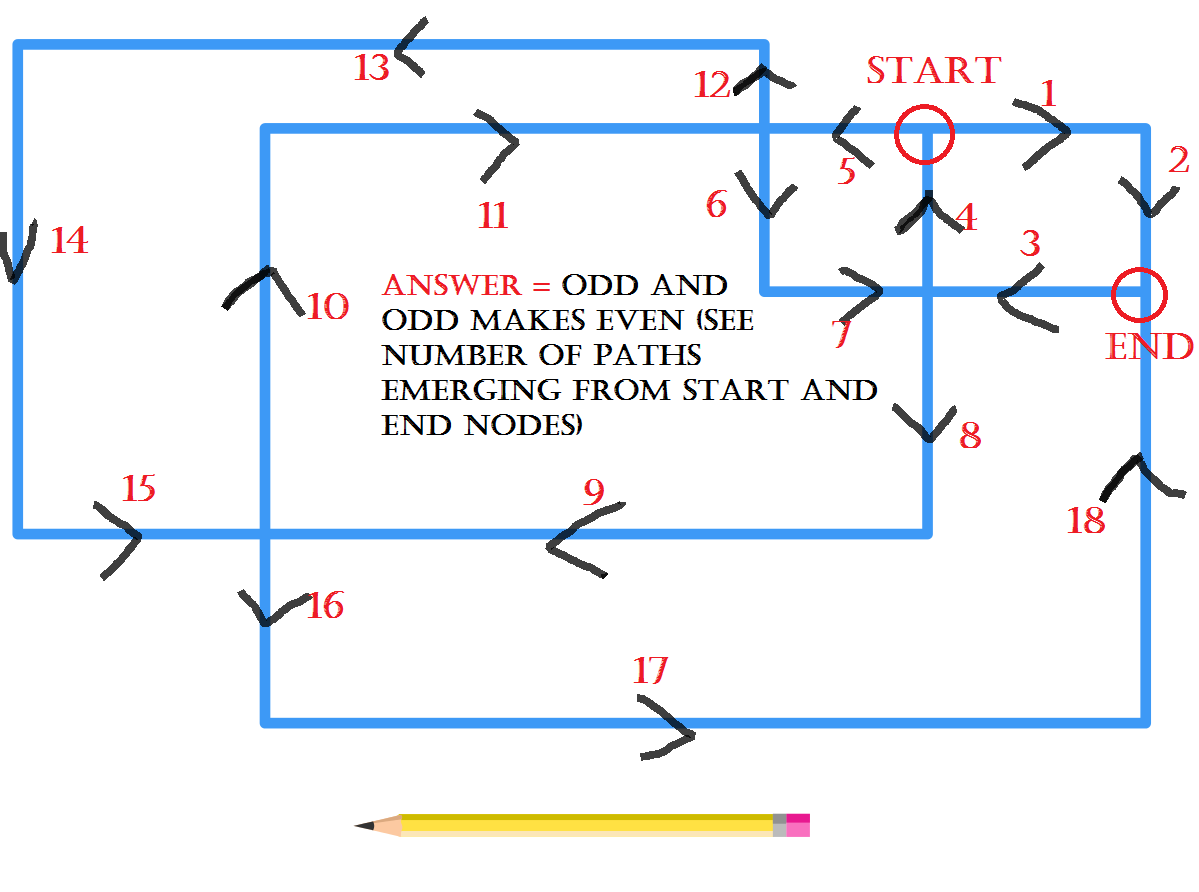
There are only two junctures which have an odd number of paths going to them. One needs to be the start, the other the end of the line. The details of the path through the other junctures may be different between solutions.
One possible solution is below. Start by drawing the black path back to starting point, then follow the red path to the end.