34 of 100: Magic Triangle Perimeter
Each of the integers from 1 to 9 is to be placed in one of the circles in the figure so that the sum of the integers along each side of the figure is 17. Determine the sum of the three integers placed in the corners.
With this kind of puzzle it helps to start with either the largest or smallest digit, and figure out what happens after they get placed.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Beautiful! Short and sweet! This surely deserves to be a top solution! :)
That's what I did too. But you have to assume that the problem can be done.
Log in to reply
I'm not seeing any issue with accepting the assumptions implied by the problem creator. "Assume X, show Y" is a fairly common way to frame a question in mathematics.
This solution is wonderful!
That's exactly what I did too!
There was even one case where in a UKMT(Maths Competition) It asked if the square of 49 was divisible by the square root of 49(it asked for the remainder, multiple choice) and I used my scrap paper working out the square of 49 and dividing by 7 and later my friend asked me 'hey what did you put there' I said I put 'zero, A' my friend asked 'how did you get there?' I told my friend that I used my paper and worked the whole thing out... then they informed me of the logic of it all... square of 49=49x49=7x7x49=divisible xD That's really what I mean by take forever to calculate the whole thing
That's really smart! I didn't think about that! I literally grabbed some paper and drew out loads of stuff xD How most people solve a problem: so if this, then this, and then this and this and this... How I solve a problem: piece of paper, calculate everything :)
Surely you also prove the existence of a solution to complete this.
Log in to reply
The problem assumes the existence of a solution. The reader isn't required to validate the assumptions of the problem creator. Not as a general rule.
super smart!
Brilliant.
I did exactly the same. I questioned the existence of the solution too, and figured that it's not difficult to determine that since there is only one triple in the set 1 to 9 that has a sum of 6.
I still don’t get it
Teach me 😞😞 help guys😡🥺🥺🥺🥺🥺🥺
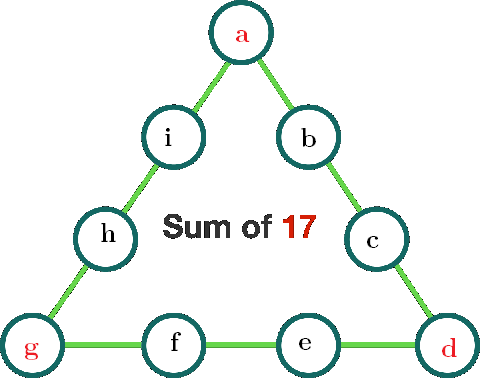
We have a + b + c + d + e + f + g + h + i = 4 5 and the sum of sides as a a + b + c + d + d + e + f + g + g + h + i + a = 3 × 1 7 ( a + b + c + d + e + f + g + h + i ) + ( a + d + g ) = 5 1 4 5 + ( a + d + g ) = 5 1 a + d + g = 6
Note: Solution edited according to @Lynn Kiaer comment.
Very good!
i finally got 1 correct!!!!!!!!!:>
This would be more straightforward if you organized the terms by pulling out the corner values, a, d and g and wrote a + b + c + d + d + e + f + g + g + h + i + a = 51 => (a + b + c + d + e + f + g + h + i) + a + d + g = 51. Then substituting 45 for the term in parentheses yields 45 + a + d + g = 51 so a + d + g = 6. But your solution is correct.
*still up voting on every solution
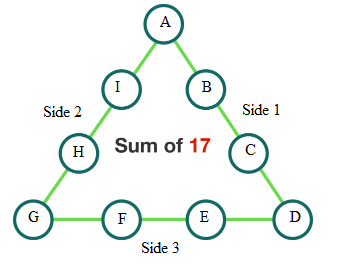
Let sum together the three sides so we get:
2 A + B + C + 2 D + E + F + 2 G + H + I = 1 7 × 3 = 5 1 = N
By the other hand the sum of number from 1 to 9 is A + B + C + D + E + F + G + H + I = 2 ( 9 ) ( 1 0 ) = 4 5 = M
∴ the sum of the corners is M − N = 5 1 − 4 5 = 6
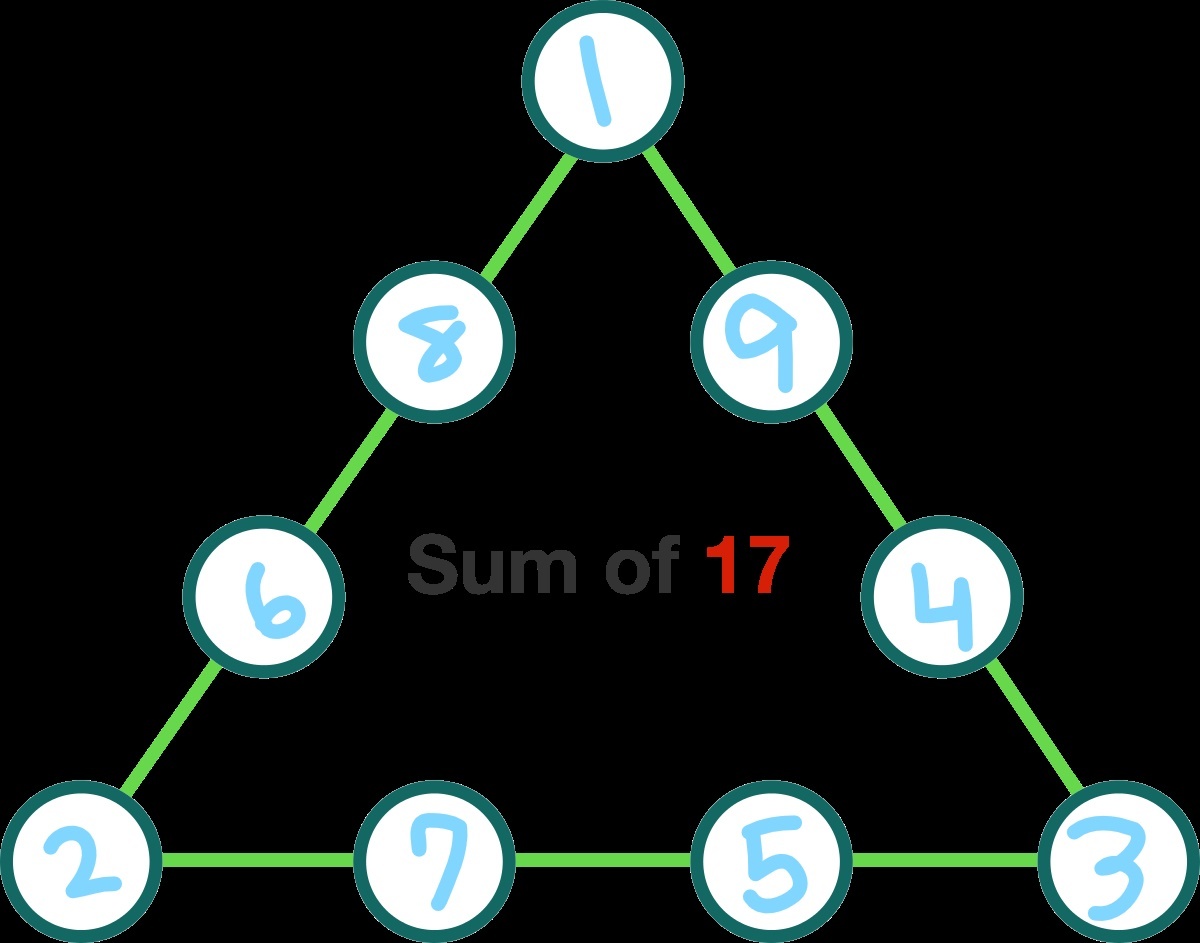 Simple guess and check.
Simple guess and check.
I also figured out a solution with guess and check. I got (clockwise from top) 3, 6, 7, 1, 5, 9, 2, 4, 8
Sum along 3 sides are each 17.
So total is 51
But 3 corners each added two times.
Sum from 1 to 9 is 45
Therefore, the necessary sum is 6
No need to place the numbers. They add to 45 (1+2 +3+...+9). The three sides add to 51 (17 *3) but in that case the corners are double counted. So the answer is 51-45 = 6.
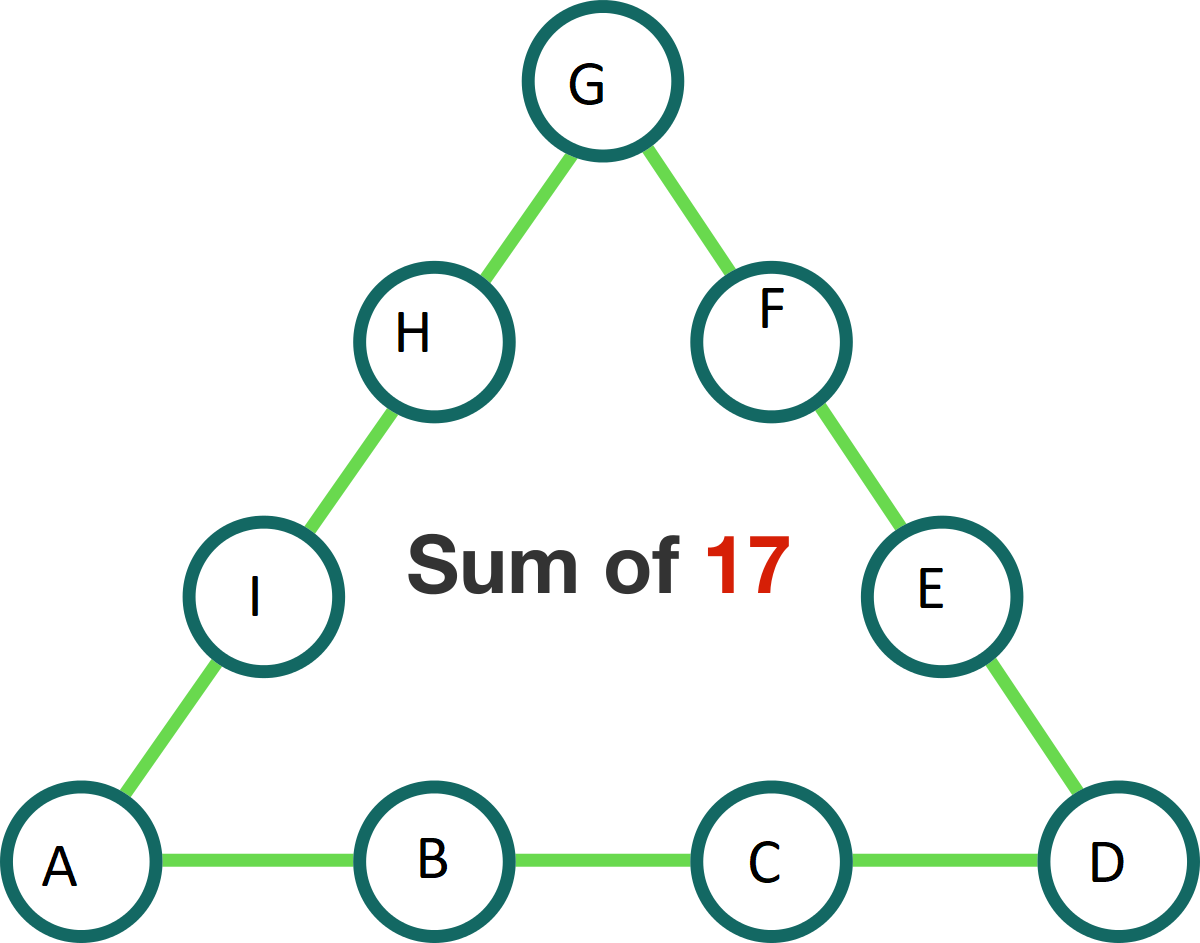
Note that 9,8,7 can't be in the same line, in fact: if 9 and 8 are in the same line 17=9+8+0+0 (impossible); if 9 and 7 are on the same line 17=9+7+1+0 (impossible); if 8 and 7 are on the same line 17=8+7+1+1 or 17=8+7+2+0 (both impossible).
So, 9,8,7 can't be in A,D,G and I have placed them respectively in I,C,F.
Now, note that the line with 9 can be (9,5,2,1) or (9,4,3,1) and the line with 8 can be (8,6,2,1) or (8,5,3,1) or (8,4,3,2)
These two lines must have only a number in common so I choose (9,5,2,1) and (8,4,3,2). The number in common is 2, so I placed it in A. Now, 1 and 5 can be placed in H or G and 3 and 4 can be placed in B or D. Considering the third line (that which contains 7), 17=7+6+3+1, the only combination which contains one of (4,1),(4,5),(3,1),(3,5). So, I placed 1 in G and 3 in D. The remaining three numbers are easy to place.
The answer is 6
There are only 7 possible combinations of 4 non-duplicated digits selected from 1-9 that add up to 17, and of those, only 3 that contain 3 pairs of duplicates that also include all 9 digits. So it's relatively trivial to enumerate them and visually scan the results for the answer.
this will be:
1
8 9
[the sum is exactly 17]
6 4
2 7 5 3
The answer is 6. To add 4 numbers with an odd sum (e.g. 17), you have to either add 3 odd numbers and one even number or 3 even numbers and one odd number. There are 5 odd and 4 even numbers in the first 9 integers, so we need two odds and one even in the corners. Start with the 3 smallest numbers 1, 2, 3 in the corners (they add up to 6), then find the 3 pairs (even, even), (odd, odd) and (even, odd) to make the missing sums of 12, 13 and 14: 5+7=12, 9+4=13, 6+8=14.
So since we need four numbers to equal 17 I split it up into the fact that we need two numbers to make 10 and two numbers to make 7 (because 10+7=17). I started with the possible ways to make 10 and 7 with two numbers:
10:
1+9
2+8
3+7
4+6
7:
1+6
2+5
3+4
Then, I started to make combinations that didn't use the same number twice and only had one matching number from the previous combinations:
1 + 9 + 2 + 5
2 + 8 + 3 + 4 (I knew 2 + 8 + 1 + 6 wouldn't work here because 1 and 2 would overlap with the first combination)
3 + 7 + 1 + 6
Then, I since 1, 2, and 3 were the only numbers that showed up twice in the combinations, I added them up because they were the corners!
1 + 2 + 3 = 6
Let E represent an even number and O an odd number. Since every side can either have 3 odd numbers and one even number or vice versa, and there have to be 4 even numbers, one of the solutions will look like this:
O
O E
O O
E E E O
If we put 2, 4 and 8 in the bottom side (with 2 being in the corner), it works out. We get 1, 2 and 3 in the corners.
Iterate through all possible permutations. That is a matter of second.
Just for your information, an example of the solved triangle would look like:
1
5 6
9 7
2 8 4 3
Of course, the sum of the three corners are equal to 1 + 2 + 3, which means the three corners add up to 6.
- \(\(\(\(\(\(\(\(\(\(\(\(\(\(\(\([LaTeX]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org]([https://brilliant.org](********************\(\frac{https://brilliant.org}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{\(\frac{denominator}{ ||denominator|| || ||row 2 col 1||row 2 col 2|| || ||row 2 col 1||row 2 col 2|| || ||row 2 col 1||row 2 col 2|| || ||row 2 col 1||row 2 col 2|| || ||row 2 col 1||row 2 col 2|| || ||row 2 col 1||row 2 col 2|| || ||row 2 col 1||row 2 col 2|| ||row 2 col 1||row 2 col 2||||||||||||||||} })})})})})})})})})})})})})})})})}) * * * * * * ))))))))))))))))))))))))))))))))
I worked too hard.
I started with a table of sets of 4 single digit numbers that sum to 17 where a number is used only once per sum.
Since the order of the digits doesn't matter for this table, requiring the digits to be an ascending order eliminates duplication. Since duplicate digits are not allowed, each possible combination can be expressed as an ascending sequence.
1, 2, 5 (since the last can't be more than 9), 9
1, 2, 6, 8
Since the next lower digit in the last place would be 7, making the 3rd place also 7, that is not allowable.
And dropping the 4th below 8 that would result in repeating previously used combinations, so we are done with rows starting 1, 2.
1, 3, 4, 9
1, 3, 5, 8
1, 3, 6, 7
1, 4, 5, 7
We have now enumerated all the possibilities that involve 1.
2, 3, 4, 8
2, 3, 5, 7
There are no more ascending sequences that add up to 17. Since every list of numbers can be arranged in increasing sequence (mumble something about well-ordered sets...) we know that all the possibilities are enumerated.
All of these ascending sequences start with 1 or 2, and all but one of the rows includes 3. This tells us that each combination must include 1 or 2, and all but one include 3. In fact, all the rows except for 1, 4, 5, 7 have two of those three numbers.
So the corners must be 1, 2, 3.
If I had remembered the exact phrasing of the question, I would have realized that I was done. But no, I continued...
I start by placing 1, 2, 3 in the corners. And then I fill one side with the remaining numbers from the first combination: 4 and 9 from 1, 3, 4, 9. I cross off all the other rows that contain a 5 or a 9, because those are no longer available.
I can't use the next row, 1, 2, 6, 8, for the other side that includes 1, because of the 2. So there is only one row left that has a 1, namely 1, 3, 6, 7. I fill the next side in with 6 and 7, and cross off the rows that have 6 or 7 in them.
There is only one row left. And it fits in the remaining side of the triangle.
THE NUMBERS STARTING WITH LEFT CORNER ARE 1 7 6 3 8 4 2 5 9. SO THE REQUIRED SUM IS 6.
explain more how you got it
I really did it by starting numbers there and tried to make left 17, then with with the new number i started on the right side till I got to the last side. I had a hunch the left vertex has to be 1 and by putting numbers on the other vertices and sometime changing numbers from the sides, I found I have to have the top vertex has to be 2 and finally tried 3 for the last vertex and by manipulation between the other numbers I arrived at my solution. Anyway thanks for your concern.
Log in to reply
Here is a simpler solution, let the sum be S, then S + 1 + 2 + ........ + 9 = 3*17, or S + 45 = 51, so S = 6.
I have provided two solutions below:
- Using simple logic rather than algebra:
- The individual numbers add up to 45
- The 3 sides add up to 51
- The corners are counted twice therefore their sum equates to the difference ie. 51-45 = 6
from the top of triangle clockwise: 1,7,6,3,4,8,2,9,5
Since sum of the integers along each side is 17, so total of all 3 sides comes to be 1 7 × 3 = 5 1 , But here each corner is added 2 times. Since sum of all integers from 1 to 9 is 45, so this difference is equal to the sum of three integers at the corners and is equal to 5 1 − 4 5 = 6