38 of 100: Curse of the Forgetful Cheater

With the two coins, there are four possible results (fair coin probability shown first):

Heads/Heads: (1/2)*(3/4) = 3/8

Heads/Tails: (1/2)*(1/4) = 1/8

Tails/Heads: (1/2)*(3/4) = 3/8

Tails/Tails: (1/2)*(1/4) = 1/8

So, surprisingly, the chance of heads/tails is 50% (two middle scenarios), and 1 out of 4 times it will be because the weighted coin came up tails ( shown in bold ). Therefore, 3 out of 4 times (3/4) it comes out tails/heads because the weighted coin came up heads.

Relevant wiki: Bayes' Theorem and Conditional Probability

This question can also be solved using Bayes' theorem. The case to be considered here is that one coin shows up heads while the other shows tails. We can list out the following two events from the given case ( let us call this case A )

$\begin{array} {|l|c|r|}\hline \text{Fair coin} & \text{Biased coin} & \text{Probability} \\ \hline \text{Heads} & \text{Tails} & \dfrac{1}{2}.\dfrac{1}{4}=\dfrac{1}{8} \\ \hline \text{Tails} & \text{Heads} & \dfrac{1}{2}.\dfrac{3}{4}=\dfrac{3}{8}\\ \hline \end{array}$

As we can observe from the table itself, the first situation is incorrect as per our assumption in the question which says " the coin showing heads is the weighted/biased coin ". Hence according to the Bayes theorem, the probability of getting the guess correct is

$\text{P(correct | A occurs)}=\dfrac{\dfrac{1}{2}.\dfrac{3}{4}}{\dfrac{1}{2}.\dfrac{3}{4}+\dfrac{1}{2}.\dfrac{1}{4}}=\dfrac{\dfrac{3}{8}}{\dfrac{4}{8}}=\boxed{\dfrac{3}{4}}$

Note: We can directly multiply the probabilities of the two different coins because their outcomes are independent of each other.

The probability that the coin showing head is the weighted coin in the 1st flip is $\frac{3}{4}$ * $\frac{1}{2}$ = $\frac{3}{8}$ .

However, we need to keep flipping the two coins as long as they show both heads OR both tails in all the previous flips. P(HH+TT) in any flip is = $\frac{3}{4}$ * $\frac{1}{2}$ + $\frac{1}{4}$ * $\frac{1}{2}$ = $\frac{1}{2}$ .

Thus, the probability that the coin showing head is the weighted coin AND 2 or more flips are required is as follows:

P(coin is the weighted coin && 2 flips are required) = ( $\frac{3}{4}$ * $\frac{1}{2}$ + $\frac{1}{4}$ * $\frac{1}{2}$ ) * $\frac{3}{4}$ * $\frac{1}{2}$ = $\frac{1}{2}$ * $\frac{3}{8}$ .

P(coin is the weighted coin && 3 flips are required) = ( $\frac{3}{4}$ * $\frac{1}{2}$ + $\frac{1}{4}$ * $\frac{1}{2}$ ) * ( $\frac{3}{4}$ * $\frac{1}{2}$ + $\frac{1}{4}$ * $\frac{1}{2}$ ) * $\frac{3}{4}$ * $\frac{1}{2}$ = ( $\frac{1}{2})^{2}$ * $\frac{3}{8}$ .

P(coin is the weighted coin && n flips are required ) = ( $\frac{1}{2})^{n-1}$ * $\frac{3}{8}$ (n>=1).

As n gets infinitely larger, the sum of all the probabilities becomes an infinite geometric series with the ratio |r|<1 since r = $\frac{1}{2}$ and the first term is $\frac{3}{8}$ . The series sums up to: $\frac{3}{8}$ * $\frac{1}{1-0.5}$ = $\boxed{3/4}$

There is no need to sum infinite series or invoke theorems, it is simply enough to look at the ratio of correct determinations against incorrect determinations. We can disregard all flips where both coins show the same sign as we merely toss again i.e. we are in exactly the same state as if we had not tossed at all.

Chance of a correct determination (HT) = $\frac{3}{4}$ * $\frac{1}{2}$ = $\frac{3}{8}$

Chance of an incorrect determination (TH) = $\frac{1}{4}$ * $\frac{1}{2}$ = $\frac{1}{8}$

Ratio of correct determination vs incorrect determination = $\frac{3}{8}$ : $\frac{1}{8}$ = 3 : 1

So overall chance of eventual correct determination = $\frac{3}{(3 + 1)}$ = 0.75 i.e. 75%

Write $h,t$ for the outcomes of the fair coin and $H,T$ for those of the biased coin.

What matters is only the last coin flip; we can simply ignore earlier outcomes, because they do not affect the odds of the final flip. We draw the correct conclusion if we flip $tH$ ; this is precisely three times more likely than drawing the wrong conclusion with $hT$ .

Therefore the odds are 3:1, a probability of $\boxed{3/4}$ .

It is not relevant how long it takes to get to the desired coin flip (one heads and one tails), all that matters is the probability of each combination occurring on that successful one:

$P(\text{Weighted H \& Fair T}) = \frac{3}{4}*\frac{1}{2} = \frac{3}{8}$

Similarly the others are calculated:

$P(\text{Weighted H \& Fair H}) = \frac{3}{8}$

$P(\text{Weighted T \& Fair H}) = \frac{1}{8}$

$P(\text{Weighted T \& Fair T}) = \frac{1}{8}$

The desired probability is $P( \text{Weighted H | one heads and one tails})$

Therefore it is $\frac{\frac{3}{8}}{\frac{3}{8} + \frac{1}{8}} = \boxed{\frac{3}{4}}$

In general, with an unweighted coin and a weighted coin that is heads N% of the time, this strategy works N% of the time.

An intuitive way of putting it is that the unweighted coin favors neither outcome.

A more formal proof: P(Heads and Tails) (in any order) = 50% because after you flip the weighted coin, the unweighted coin will match half the time.

P(Fake coin Heads and Real coin Tails) = N% * 50% (Just multiply the probabilities)

P(Fake coin Heads and Real coin Tails)/ P(Heads and Tails) = N% * 50 % / 50% = N%

probability of having weighted head = probability of having weighted head and probability of NOT having fair head.

thus, prob of having weighted head = 3/4 * (1 - 1/2) = 3/8

probability of having fair tail = probability of having fair tail and probability of NOT having weighted tail

thus, probability of having fair tail = 1/2 * (1 - 3/4) = 3/8

thus, probability of having weighted head and fair tail = probability of having weighted head + probability of having fair tail = 3/8 + 3/8 = 3/4

The possible scenarios could be: 1- Weighted: head Fair: tail this is the wanted situation possibility of this is: 3/4 x 1=3/4

Note: situations in which the side of coins are the same must be eliminated according to the question so, when a coin is on head the other one must be on tail.

Let $A$ be the fair coin and $B$ be the unfair coin. $H =$ heads & $T =$ tails. In every time you flip the two coins you have four different cases to consider: (A, B) could be 1- (T, T) with the probability of $\frac{1}{2}$ * $\frac{1}{4}$ ,

2- (H, H), with the probability of $\frac{1}{2}$ * $\frac{3}{4}$ ,

3- (H, T) with the probability of $\frac{1}{2}$ * $\frac{1}{4}$ ,

or 4- (T, H) with the probability of $\frac{1}{2}$ * $\frac{3}{4}$

Knowing that one of them is H and the other is T, we need to consider only 3 and 4. So the probability = the probability of 4 divided by the probability of (3 $+$ 4) which is equal to $\frac{3}{4}$ .

If u take 4 times First coin out comes:H H H T Second coin outcomes:H H T T Total 16 in sample space. The favorable are those in which one H and one T appears which happens to 8 Hfrom first and T from second (6 in total)+ T from first and H from second ( 2 in total) now out of this 8 what arevtge cases in which H is actually from weighed( first) ? It is 6 Hence the prob:6/8=3/4

The solution is really easy to understand. We stop at a Point, where just two of the four possible combinations exist. That means, that the probality for finding the wrong coin and the right one are together 1. So we can ignore the $\frac{1}{2}$ probability of the normal coin and just use the probability for the weighted coin.

Listing the fair coin first, you either see HT or TH. Both outcomes of the fair coin are equally likely, so ratio of the likelihoods of your two possibilities is the ratio of the outcomes of the unfair coin, 3:1. Listed as a probability, that's $\frac34$ vs. $\frac14$ .

• In probability I feel it's dangerous to think intuitively, but.....
• Intuitively, if you flip the coins and get H-T, there are only 2 options:
• (1) the coin shows H is the weighted coin [w:H , f:T]
• or (2) the coin shows T is the weighted coin [w:T , f:H]

• The probability that the weighted coin shows head is 0.75. The fair coin shows H\T in the same probability, so it does not have any effect, and that's why the probability the weighted coin shows H given one coin shows H and the other T is 0.75 too.

• To be sure, I checked the probability that the weighted coin shows head P[w:H,f:T], given one coin shows H and the other T P[w:H,f:T]+P[w:T,f:H] (The results of flipping the coins is independent).

• P[w:H,f:T]=0.75*0.5=0.375
• P[w:H,f:T]+P[w:T,f:H]=0.75 0.5+0.25 0.5=0.375+0.125=0.5
• $\frac{0.375}{0.5}$ =0.75

For the fair coin, the probability of heads (H) or tails (T) is $\frac{1}{2}=\frac{2}{4}$ (i.e. HHTT), whereas the probability for the weighted coin is $\frac{3}{4}$ (i.e. HHHT). Thus the options that result in one heads and one tails are:

Assuming the coin showing heads (H) would be correct in 6 of the 8 combinations as each coin flip is independent. $\frac{6}{8}$ simplifies to $\boxed{\frac{3}{4}}$ .

With the two coins, there are 8 possible results.

Four of those 8 possible results have the 1 Head and 1 Tail as required. In $\frac{3}{4}$ of those possibilities, the weighted coin is heads while the fair coin is tails.

Therefore, the technique would work $\frac{3}{4}$ of the time.

I did a simple list of 8 possibilities (since biased has 4 events) and counted 3 winning results (T/H) and one false positive (H/T). The other results would not matter since we would not stop flipping on a matching set of heads or tails.

normal/Biased.
H/H
H/H
H/H
H/T.
T/H
T/H
T/H
T/T

First of all, we can ignore all flips before the final one. The flips are independent and do not affect each other at all, so the question is equivalent to: Given that we have just flipped these coins and gotten one head and one tail, what are the chances that the coin showing heads is the weighted coin?

Now, there are two ways to produce one head and one tail: either the weighted coin shows heads and the normal coin shows tails, or the weighted coin shows tails and the normal coin shows heads. We want to know: What is the probability of the first outcome given that we get one of these two outcomes?

The first outcome has probability 3/4 * 1/2 = 3/8.

The second outcome has probability 1/4 * 1/2 = 1/8.

The probability of getting one of these outcomes is thus 3/8 + 1/8 = 1/2.

Therefore, the probability of getting the first outcome (p=3/8) given that we got one of the two (p=1/2) is (3/8) / (1/2) = 3/4.

Using the notation of lowercase letters representing the outcomes of the fair coin, h and t, and uppercase letters representing the outcomes of the weighted coin, H and T, this problem can conveniently be modeled as a 4-sided die and fair coin problem because the probabilities of the two events are independent. The 4-sided die has three sides labelled H and one side labelled T. A state diagram can show the probabilities of the 8 possible outcomes (see below). Only 4 of the 8 possibilities are significant (i.e. an outcome that involves a head and a tail). Three of the 4 significant outcomes correctly identify the weighted coin, tH. The other outcome, hT, of the significant outcomes, is deceptive. Therefore, this method has a 3/4 chance of being "correct".

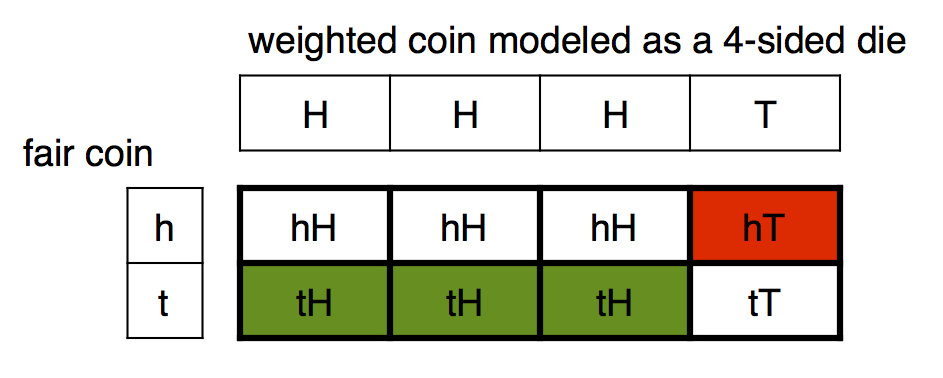
The probability of guessing the coins correctly on the first flip is $\frac{3}{4} \cdot \frac{1}{2}=\frac{3}{8}$ You will only flip again if the 2 coins have the same side facing upward, so the probability of flipping again is $(\frac{3}{4} \cdot \frac{1}{2})+(\frac{1}{4} \cdot \frac{1}{2})=\frac{3}{8}+\frac{1}{8}=\frac{1}{2}$ . Now, we can form a geometric series representing the probability of choosing the write coin. $\frac{3}{8}+(\frac{1}{2} \cdot \frac{3}{8}) + ((\frac{1}{2})^2 \cdot \frac{3}{8}) + ((\frac{1}{2})^3 \cdot \frac{3}{8}) +.... \\ \frac{\frac{3}{8}}{1-\frac{1}{2}} = \frac{\frac{3}{8}}{\frac{1}{2}} = \frac{3}{8} \cdot 2 = \boxed{\frac{3}{4}}$

If we note down all the possibilities, We get H T, H H, H T, T H, H H, H T, H H, T T. In the first four possibilities three times we get a head and tail combination out of which we get two of them correctly identified. In the next four possibilities we get a single head and tail combination which we get correctly identified. The first four and the next four are listed differently because there is an equal possibility for the weighted coin and fair coins combination to be a TH and TT. So, out of four combinations three are identified correctly. This is why we have a 3/4 possibility of identifying the weighted and the fair coins correctly.

I found the solution with the aid of a state diagram, but unfortunately I lack the skills to post. So here it is written out:-

At the first flip of the coins there are three possible outcomes:-

hT = 1/2 * 1/4 = 1/8 = leads to incorrect assumption

tH = 1//2 * 3/4 = 3/8 = leads to correct assumption

tT or hH = 1/2 * 1/4 + 1/2 * 3/4 = 1/2 = requires a re-flip

where h and t are the heads and tails probabilities of the fair coin H and T are the heads and tails probabilities of the weighted coin

Therefore we have an infinite series of possible re-flips, each with a probability of 3/8 of leading to a correct assumption and 1/2 of requiring another re-flip. i.e. We have:-

3/8 * (1 + 1/2 + 1/4 + 1/8 + .......) = 3/8 * 2 = 3/4

Essentially, the probability of getting heads or both tails in n-1 trails is a common weighting factors for both cases and works out as a geometric progression with ratio 1/2. So, the probability of the biased coin showing heads first goes as (3/4) * (1/2) *[ 1 + 1/2 + 1/4 + ..........] The probability of the unbiased coin showing heads first goes as (1/4 * (1/2) * [1+ 1/2 + 1/4 + .......] So, the odds of the biased coin showing heads first is 3 : 1 Hence the probability of the above is 3/4