39 of 100: Stairway to Puzzlement
A unit cube with side lengths of 1 is cut into cuboids as shown, with the pieces placed adjacent to form a staircase. The total surface area of the original unit cube is 6. What is the total surface area of the new figure?
There's a clever approach to keep down the number of calculations you need.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Nice solution.
Exactly how I thought of it, nice description!
Any cut adds two new faces. The three pieces, separate, have a surface area of 6+2+2 = 10.
The overlapping parts after the joinings account for 2* 6 1 and 2* 3 1 .
6 2 + 3 2 = 3 1 + 3 2 = 1, so the result is 10 - 1 = 9.
Steps:
1) Start with the full cube: Surface area = 6
2) Take the thickest piece off of the intermediate piece, uncovering 2 units. 6 + 2 = 8
3) Take the intermediate piece off of the thinnest piece, uncovering 2 more units. 8 + 2 = 10
4) Put the thickest and intermediate pieces together, covering back up
2
×
3
1
units.
1
0
−
3
2
5) Put the intermediate and thinnest pieces together, covering back up
2
×
6
1
=
3
1
units.
1
0
−
3
2
−
3
1
=
9
There are additional area of 2 for each cut that makes it 4 more than the original hence it should be 10 not 9
Log in to reply
Which steps are you referring to (from my list)?
(1x6) + (1x4) - (1/6 + 1/3)x2 = 10-1 = 9
from the front view:1/6 +1/6 +2/3 =1 and the back side:1 and top & bottom:6 and left & right:2
so, the surface area of the new figure is= 1 + 1 + 6 + 2 = 9
I would just like to point out that 1+1+6+2=10 not 9 in your solution.
It should be "area" in the second sentence...but it is obviously understood...just a typing error.😊
the front view: 6 1 + 6 1 + 3 2 =1 the back side:1 top & bottom:6 left & right:2 1 + 1 + 6 + 2 = 9
Full breakdown of maths
1+1=2 ----- 2*3 = 6 This is for the top and bottom of each blue sections.
2 1 * 3 = 1.5 For the 3 darkest blue sides.
3 1 * 2 = 0.666r For the 2 medium blue sides.
6 1 * 3 = 0.5 For the 3 lightest blue sides.
1.5 + 0.667 + 0.5 = 2.666r
1/2 - 1/3 = 0.1666r For the front dark blue side that is partially blocked by the medium blue block.
1/3 - 1/6 = 0.1666r For the front medium blue side that is partially blocked by the lightest blue block.
0.1666r + 0.1666r = 0.333r
Final answer = 6 + 2.666r + 0.333r = 9
(Note: r stands for recurring)
Surface area = area which can be touched i.e., 6 faces in this structure
-
From front of the staircase = 6 1 + 6 1 + 6 1 = 2 1
-
Left of the staircase = 6 1 + 3 1 + 2 1 = 1
-
Right of the staircase = 6 1 + 3 1 + 2 1 = 1
-
Back of the staircase = 2 1
-
Top of the staircase = 1 + 1 + 1 = 3
-
Bottom of the staircase = 1 + 1 + 1 = 3
Total surface area = 2 1 + 2 1 + 1 + 1 + 3 + 3 = 9
To keep the calculations down, think in terms of pairs: Front/Back, Left/Right, Top/Bottom. Then think of the simplest way to represent each face.
- Surface area = 6 thus each square has area 1, and is 1x1.
- Top/Bottom is simply 3 of the original square faces: 2x3 = 6
- Left/Right are the three colors which add up to one square face: 2x1 = 2
- Front/Back has potential for confusion when viewed from the front, so just look at the back, a half-square: 2x(1/2) = 1
- Sum is 6+2+1 = 9
LaTeX: the area A 1 is compound of 6 squares of the same size.
LaTeX: Let n the length of the cube side or the square side
LaTeX: A 1 = 6 n 2 = 2 n 2 + 4 n 2 = 2 n 2 + 4 ( 2 n 2 + 3 n 2 + 6 n 2 )
LaTex: Let ( a = 2 n 2 ) , ( b = 2 n 2 ) , ( c = 3 n 2 ) and ( d = 6 n 2 )
LaTex: We get : A 1 = a + 4 ( b + c + d )
LaTeX: As you can see, the cube is split into 3 cuboids to represent a staircase
LaTeX: But the upper and lower areas don’t change : a is multiplied by 3
LaTeX: Facing the staircase, 2 areas are half hidden : b and c
LaTeX: b is partially hidden by c and c is partially hidden by d
LaTex: We get : ( b − c ) + ( c − d ) + d = b
LaTex: It was easy to guess. The area represents the back of the staircase, that is to say : b
LaTex: The areas of the 2 sides of the staircase are : 2 ( b + c + d )
LaTex: We have now a new area : A 2 = 3 a + 2 b + 2 ( b + c + d )
LaTex: A 2 = 6 n 2 + 2 2 n 2 + 2 n 2 = 9 n 2
LaTex: As : n = 1 , the new area is : A 2 = 9
Separating the three cuboids, we have a total surface area of 2 + 4 * 6 1 + 2 + 4 * 3 1 + 2 + 4 * 2 1 = 2 * 3 + 4 ( 1 ) = 10 . Then we take out the double counted areas which are 2 * 6 1 + 2 * 3 1 = 2 * 2 1 = 1 . Hence, the required surface area = 9.
6+4(1)(1)-2(1/3)(1)-2(1/6)1=9
Orienting as if you are going to walk up the stairs we will look at the total areas facing in each direction.
Top and Bottom are easy, 3 squares of area 1, 3 square units each.
The Left and Right surfaces are just the original left and right sides of the cube redistributed so these are 1 square unit each.
The Back is a rectangle 1 unit wide and 1/2 unit high so that has area 1/2.
The three exposed front surfaces actually can be visualized as "covering" the back rectangle. The areas of the pieces sum to another 1/2.
Surface Area =3+3+1+1+1/2+1/2 =9
Original cube, Top+Bottom=2,.
New figure, Top+Bottom=6,.
Original cube, Left+Right=2,.
New figure, Left+Right=No change=2,.
Original cube, Front+Back=2,.
New figure, Back = 1/2,.
So, Front = Back = 1/2,.
New figure, Total = 6 + 2 +(1/2)+(1/2),.
= 9.
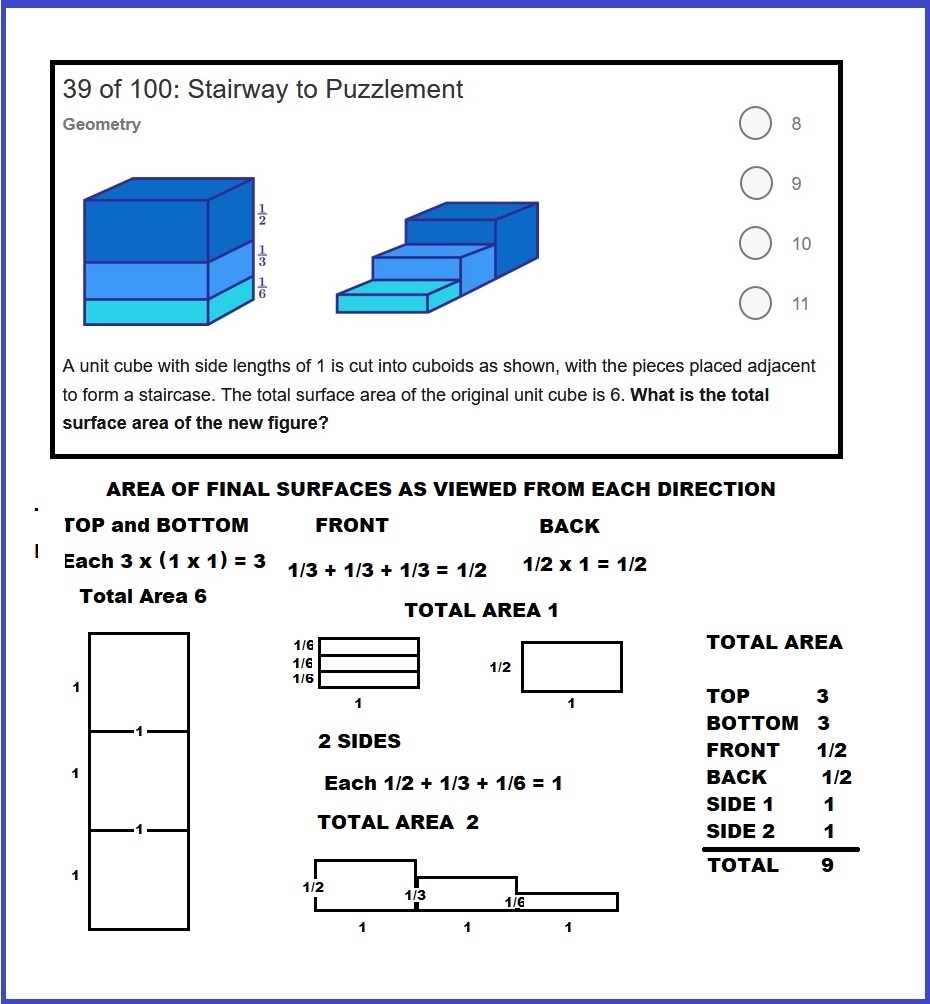
If the full cube has area 6, each side of it has area 1.
Top and bottom contribute 3 each to the area, as each square is full size. Total contribution 6. Left and right add 1 each, as
2
1
+
3
1
+
6
1
=
1
and the width is also 1. (Just think, it was 1 to start with, so moved around it is still 1.) Total added 2.
Left and right add 1 each, as
2
1
+
3
1
+
6
1
=
1
and the width is also 1. (Just think, it was 1 to start with, so moved around it is still 1.) Total added 2.

Front and back amount to area of 2 1 each, as the darkest rectangle is 2 1 high and 1 wide. From the back you see the 2 1 × 1 rectangle of dark blue, from the front the three stacked to the same amount as shown in the figure. Total addition 1.
Total 6 + 2 + 1 = 9 .