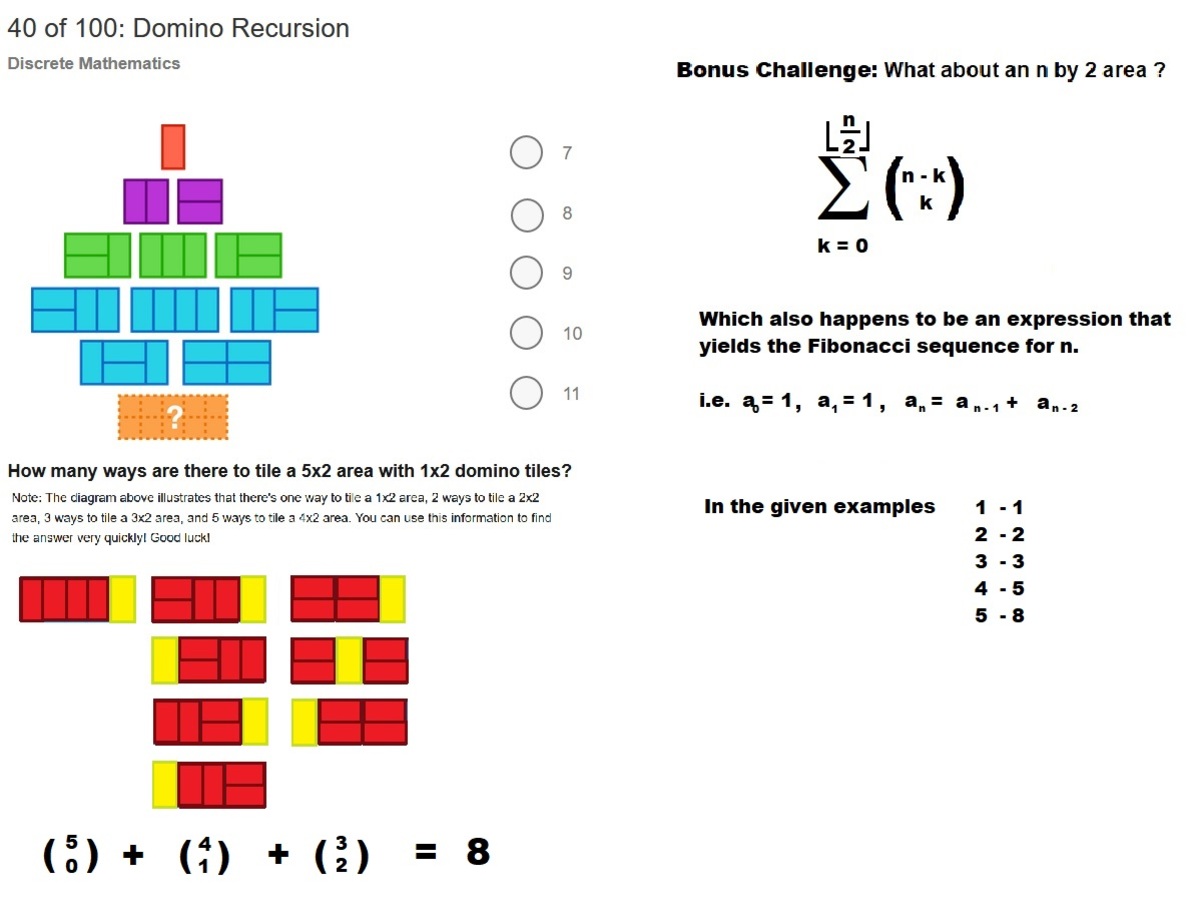
40 of 100: Domino Recursion
How many ways are there to tile a 5x2 area with 1x2 domino tiles?
Note: The diagram above illustrates that there's one way to tile a 1x2 area, 2 ways to tile a 2x2 area, 3 ways to tile a 3x2 area, and 5 ways to tile a 4x2 area. You can use this information to find the answer very quickly! Good luck!
Use what's known to help solve for what's unknown!
Bonus challenge: What about an n by 2 area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Elegant solution. Another method is the following :
Number of ways of decomposing 5 into 1 or 2 or 0 (A 2 will be followed by a zero). We just need to consider 1 row since any choice of the top row constrains the bottom.
5 can be decomposed as follows :
1 + 1 + 1 + 1 + 1, 2 + 1 + 1 + 1, 1 + 2 + 1 + 1, 1 + 1 + 2 + 1, 1 + 1 + 1 + 2, 2 + 2 + 1, 1 + 2 + 2, 2 + 1 + 2
giving a total of 8 ways
Log in to reply
Good method! Deserves to be a top answer.
Log in to reply
Thanks. The Fibonacci solution is great but it did not occur to me at that time. What occured to was the link to the number partitioning problem but in my hurry , i did not work through it fully and i tried the pattern recognition approach & guessed (2n -1). Later i worked out the combinations. The number partition method is more cumbersome but possibly gives insight into other problems which may be useful in problems where purely geometric reasoning would be difficult (triminoes for example and polyminoes in general)
Nice idea! To count partitions, divide the partitions (lol) in three cases: 1-all 1s. This can be done in one way; 2-one 2, as in 2+1+1+1. There are four places for the 2, so 4 ways to partition five with these numbers; 3- two 2s, as in 2+2+1. There are three places for 1, accounting to 3 ways. The total is 8 ways.
great solution! Thanks for sharing new knowledge to me :) !
Another way you can solve it is to use the given information about the ways to construct a 4x2, 3x2 and 2x2. You can add a vertical domino to the end of any of the 5 4x2 domino to create a 5x2. You can also add a 2x2 combination to the 3x3 combination. Notice, if we add a 2x2 with both vertical blocks, we can construct the same shape by adding a vertical block to the end of the corresponding 4x2 shape. Therefore, we can only add the 2 horizontal blocks to the 3x3 combinations. This gives us a total of 5 + 3 = 8 combinations.
Beautiful!
How did your thinking proceed when you found that adding two dominoes vertically shouldn't be considered?
Log in to reply
Starting with two dominoes vertically what's counted in starting tiling with one domino vertically!
Very lucid. Excellent. Very well done! Regards, David
Did I understand that ?
Um... Wut?
I saw 1,2,3,5. I immediately recognized Fibonacci sequence. Also that domino example is an example from Concrete Math book by Knuth, Graham and Ptashnik.
I saw prime numbers (technically not one but still) and put 7
I did the same thing!
Brilliant - I never spotted this - I bow to your superior synthetic abilies
Because this is only 5x2, we can draw this out and do not need a formula. The first layout is to have all five tiles arranged vertically. If we wish to rotate a tile horizontally, we will need to have two tiles rotated horizontally, which will leave three tiles vertical. The pair of horizontal tiles will need to be stacked with 0, 1, 2, or 3 of the vertical tiles to their left, which is four layouts. Because there is the possibility of rotating two pairs horizontally, that will leave one lone tile vertically oriented. That tile can be to the left, between, or to the right of the horizontal tiles, which gives three layouts. Adding them, we get 8 possible layouts.
Since we know all 5 ways to fill a 4x2 area, we just need to add one vertical 1x2 rectangle to the existing patterns. Here they are:
-
1st diagram -- add one vertical to either side (2 solutions)
-
2nd diagram -- add one vertical anywhere (1 solution)
-
3rd diagram -- add one vertical to either side (2 solutions)
-
4th diagram -- included in diagrams 1 and 3 (0 solutions)
-
5th diagram -- add one vertical to either end or middle (3 solutions)
Total -- 8 solution
This is how I tried - I failed cos I included 2 impossible solutions in your step 4. Love common sense approach over complicated maths
The following formula generates an answer to the problem for any n (and, incidentally, the Fibonacci sequence):
∑ i = 0 ⌊ n / 2 ⌋ ( i n − i )
Explanation: For a given n, the possible arrangements can be described as follows:
-
All dominoes are vertical - 1 arrangement
-
1 pair of dominoes horizontal: The number of positions for this pair is equal to n-1, so the number of possible arrangements is ( 1 n − 1 )
-
2 pairs of dominoes horizontal: The number of positions for these pairs is equal to n-2, so the number of possible arrangements is ( 2 n − 2 )
-
... up to floor(n/2), because after that we run out of dominoes.
Noting that ( 0 n − 0 ) = 1 , the sum of all possible arrangements can be expressed as the sum above.
The problem can be solved intuitively by looking at the "Note" portion -- 1, 2, 3, and 5 are the first terms of the Fibonacci sequence.
The correct answer is 9. By adding one to each end of the 4x2 blocks, except the straight row obviously. Simple solution and the correct one.
The Fibonacci number
F
n
+
1
shows the number of ways
2
×
1
dominos cover
2
×
n
area as illustrated above. Since
n
=
5
⟹
F
6
=
8
. Thus, there are
8
ways as shown.
The set of figures shows that the side length of 2 is either on the left or right side. Thus, rotations of rectangular "tiles" are not necessarily counted. Let's focus on the bottom part. There are cases:
(1) The tile is composed of 5 dominoes; thus, the bottom part comprises 5 bottom sides of dominoes each measuring 1: 1 way to construct a tile
(2) The tile is composed of 3 dominoes in vertical position (bottom side measuring 1) and 2 dominoes in horizontal position (bottom side measuring 2); thus, the bottom part comprises the combination of 3 bottom sides of dominoes in vertical position and 1 bottom side of domino in horizontal position: 3 ! 4 ! = 4 ways to construct those tiles
(3) The tile is composed of 4 dominoes in horizontal position (bottom side measuring 2) and 1 domino in vertical position (bottom side measuring 1); thus, the bottom part comprises the combination of 2 bottom sides of dominoes in horizontal position and 1 bottom side of domino in vertical position: 2 ! 3 ! = 3 ways to construct those tiles
Add all the results of these cases: 1 + 4 + 3 = 8 ways to construct 5 by 2 tiles
Easy to visualize this if you notice that the second row doesn't matter. So it comes down to how many ways can you fill five squares with singles or doubles. There is one with five singles, 4 with one double and 3 with two doubles.
1, 2, 3, 5 is part of Fibonacci sequence. Next from Fibonacci sequence is 8
I got this because this is an example of the Fibonacci sequence where the numbers are: 1,1,2,3,5,8...
Either all tiles are vertical and there is 1 way of achieving this. Or you arrange 2 of the tiles horizontally, for which there is one block of horizontal tiles, which can start from the left side either at the 1st column, the 2nd column, the 3rd column or the 4th colomn. So 4 ways of achieving this. Or most of the tiles can be horizontal with only one block of vertical tiles, these vertical tiles can be in the 1st column, the 3rd column or the 5th column. So 3 ways of achieving one block of vertical tiles. So 1 + 4 + 3 = 8. | I am aware that this does not make any general way of calculating the number of ways of placing tiles on nx2 tiles, so maybe another solution will give this answer. But for the question posed this does what is needed. Regards, David Ps The very 1st solution gives the general answer, and is very lucid!
There is a pattern
x n = x n − 1 + x n − 2
Then, 3+5=8
The nuber of ways to tile an area goes up in the Fibonacci sequence which is 1, 1, 2, 3, 5, 8, etc. the number which you are on add the previous number will equal the next number so if there are 5 ways to tile a 4x2 area and 3 ways to tile a 3x2, it will be 5+3 ways which equal 8 ways to tile a 5x2 area
The general solution is ϕ n + Φ n , for n by 2 area.
Notice that horizontal dominoes have to come in pairs, if we use the condition that n 2x1 dominoes are needed to fill the 2xn area. Using an abstract notation where "1" represents one vertical domino and "2" represents a pair of horizontal dominoes, the solutions can be enumerated as:
11111 - 5 vertical dominoes only has 1 solution.
2111, 1211, 1121, 1112 - one pair of horizontal dominoes has 4 solutions.
221, 212, 122 - two pairs of horizontal dominoes has 3 solutions.
1 + 4 + 3 = 8.
Also notice that this notation enables us to enumerate the number of possible solutions using factorials: 11111 -> 5!/(5!•0!) = 1, 2111 -> 4!/(3!•1!) = 4, 221 -> 3!/(1!•2!) = 3.
With these tools, one can solve the bonus challenge by tapping into Pascal's triangle and how that leads to the Fibonacci sequence ... Try it!
Here's another challenge: use 3x1 dominoes in 3xn areas, what function characterizes the nth solution?
An even better challenge: use Hx1 dominoes in Hxn areas, what function characterizes the nth solution?
Using 1 x 2 area, there are 7 ways to tile 4 x 2 areas to make it a 5 x 2 area without repetition. Using 2 x 2 areas, there are 1 way to tile 3 x 2 areas to make it a 5 x 2 area without repetition. So total number is 7 + 1 = 8 ways.
Let F n be the number of ways to tile a n by 2 area, where n > 2 . There are two ways to start your tiling from the leftmost edge:
A) You can place a domino vertically. Then there are F n − 1 ways to tile the rest of the area.
B) You can place two dominoes horizontally and there are F n − 2 ways to tile the rest of the area.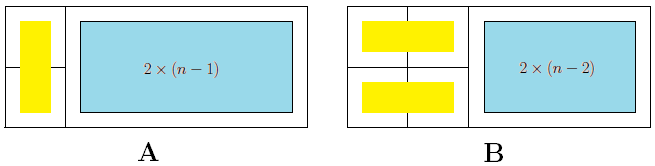 Thus there are
F
n
=
F
n
−
1
+
F
n
−
2
ways to tile a
n
by 2 area. Its the Fibonacci sequence!
Thus there are
F
n
=
F
n
−
1
+
F
n
−
2
ways to tile a
n
by 2 area. Its the Fibonacci sequence!
For the 5 by 2 area we have F 5 = F 4 + F 3 = 5 + 3 = 8 .