42 of 100: Die Even Harder

Number Theory Level 1

You have two containers, one which can hold 11 liters of water and the other of which can hold 13 liters. You also have access to a sink with a faucet. You can do any of these three things as many times as you like:

Fill one of the containers to the top with water.
Completely empty one of the containers into the sink.
Pour the contents of one container into another until the second container is full (or until the first container is empty).

Given these conditions, is it possible to measure out exactly 8 liters?

If this puzzle seems familiar, it might be because a version of this challenge was featured in the third "Die Hard" movie.

Yes No

19 solutions

Kevin Guo
Jul 11, 2017

Fill the 13-liter bottle.
Pour 11 liters into the 11-liter bottle. This leaves 2 liters of water remaining in the 13-liter bottle.
Empty the 11 liter bottle.
Pour the 2 liters of water into the 11-liter bottle.
Fill up the 13-liter bottle again and pour 9 liters into the 11-liter bottle. This leaves 4 liters of water in the 13-liter bottle.
Repeat steps 1-4 to obtain 6 liters and eventually 8 liters.

Good solution,can be made more clear by editing the steps so that each iteration(getting 4 liters first, then 6 liers, then finally 8 liters in 13-liter bottle) is clear separate step with different numbers of waters getting transferred and remaining. It cannot really be achieved by repeating steps 1-4 the way they are worded currently.

Ajit Deshpande - 3 years, 11 months ago

Surely one needs a third container?

A Former Brilliant Member - 3 years, 9 months ago

After step 2, you forgot to empty the 11-litre bottle. We should understand, but it's a little confusing...

Angel ONG - 3 years, 11 months ago

you repeat steps 2-5 not 1-5. please fix even though people will probably understand :)

Rhys Denno - 3 years, 11 months ago

But where are you keeping the 4 liters that you get in each set of 4 steps. The puzzle does not seem to allow for an additional container in which to put the water from step 4. Step 2 requires an empty 11 liter bottle unless Option 3 opens up the option of a 3rd bottle. Apologies - I didn't read your solution carefully enough.

Pauline Gleimius - 3 years, 10 months ago

I agree with the Ray Weston, this solution will require a 3rd bottle. The only way I can see to get 8 L with only 2 buttons is to get the first 4 L in the 13 L bottle as described in this solution, then transfer that 4 L to the 11 L bottle, mark the 4 L level in the 11 L bottlethen empty it. Start the procedure again and when you have 4 L in the 13 L bottle for the 2nd time, fill the emptied 11 litre bottle to the previously marked 4 L level and then tip that back into the 13 L bottle that's already got 4 L in it.

Mario D'Cruz - 3 years, 9 months ago

Oops, sorry! I'll do that @Angel ONG

Kevin Guo - 3 years, 11 months ago

Kazem Sepehrinia
Jul 11, 2017

Relevant wiki: Linear Diophantine Equations

Puzzle can be translated to: Does the equation $13x+11y=8$ have integer solutions?

Answer is "yes". Because according to Bezout's Identity we have $\gcd(13, 11) \mid 8$ .

How this relates to the puzzle: For measuring $8$ liters you have to fill or empty each of containers several times (pouring from one container to another is not considered filling or emptying).

Suppose that you fill 13 liter container $a$ times and empty it $b$ times. So the amount of the water used is $13(a-b)$ liters here. And if you fill 11 liter container $a'$ times and empty it $b'$ times during the process, then the amount of the water used is $11(a'-b')$ liters.

You have measured $8$ liters with these actions. Thus, $13(a-b)+11(a'-b')=8$ . Or even simpler $13x+11y=8$ , where $x$ and $y$ are some integers.

Notice that for this puzzle we have $a=4, b=0, a'=0, b'=4$ or $x=4, y=-4$ as the plenty of solutions have showed this.

Could you possibly explain a little more why the equation relates to the problem? (It doesn't need to be lengthy, but I fear some of the audience won't understand the connection.)

Jason Dyer Staff - 3 years, 11 months ago

Actually sir Arjen Vreugdenhil did this in his solution.

Sure. I was too lazy to do this :)) Please see if my explanation is good.

Kazem Sepehrinia - 3 years, 11 months ago

That's fine. And a fair number of users check the first 3 but no farther (at the moment Arjen's isn't in the top 3).

Jason Dyer Staff - 3 years, 11 months ago

good job thanks again

A Former Brilliant Member - 3 years, 10 months ago

sorry but i cant understand how this is possible . this is applicable only when you have another container . i.e 4(13) - 4(11) = 8 and 13 - 11 = 2 But there must be another container in which you can store the two litres obtained from the two containers ( 13 and 11 litres) repeating which 8 litres can be obtained. please correct me if i am wrong.

guru vignesh - 3 years, 9 months ago

Look at the process that @Kevin Guo has provided. In that process we fill 13 liter container four times and also empty 11 liter container four times. That's what I predicted using a linear Diophantine equation. Notice that in the process there is no third container.

Kazem Sepehrinia - 3 years, 9 months ago

o thank you

guru vignesh - 3 years, 9 months ago

There is a little mistake : you cannot say gcd(11,13) divides 8 for gcd(11,13) = 1, but you can say gcd(88,104) or gcd(44,52) divides 8.

To solve Bezout's identity, you have to solve it in 2 times.

First one : Using the euclidean algorithm : LaTeX: $11x + 13 y = 1$ Then you notice LaTeX: $gcd(11,13) = 1$

LaTeX: $13 = 11 \times 1 + 2 \Leftrightarrow \boxed {\color{#D61F06}{-1}\color{#333333}{ \times} 11 +\color{#D61F06}{1} \color{#333333}{ \times 13 = 2}}$

LaTeX: $11 = 2\times5 + \color{#3D99F6}{1} \; \color{#333333}{ \text {The remain is}} \; \color{#3D99F6}{1} \color{#333333}{\text {, then you stop dividing}}$

Second time, you have to get 8 :

In order to get 8, you need to multiply each member of the equation by 4 :

LaTex: $\color{#D61F06}{-4}\color{#333333}{ \times} 11 +\color{#D61F06}{4} \color{#333333}{ \times 13 = 8}$

And to conclude, you can say LaTeX: $\Large \boxed { \color{#D61F06}{gcd(44,52) = 4 \; \text {and} \; gcd(44,52) \; \text {divides} \; 8 } }$

Frédéric Deleria - 3 years, 11 months ago

$\gcd(11, 13) \mid 8$ guarantees that the equation $11x+13y=8$ has integer solutions.

Kazem Sepehrinia - 3 years, 11 months ago

Great Kazem, I get it : the is the condition required to solve the diophantine equation.

Frédéric Deleria - 3 years, 11 months ago

Anant Dixit
Jul 12, 2017

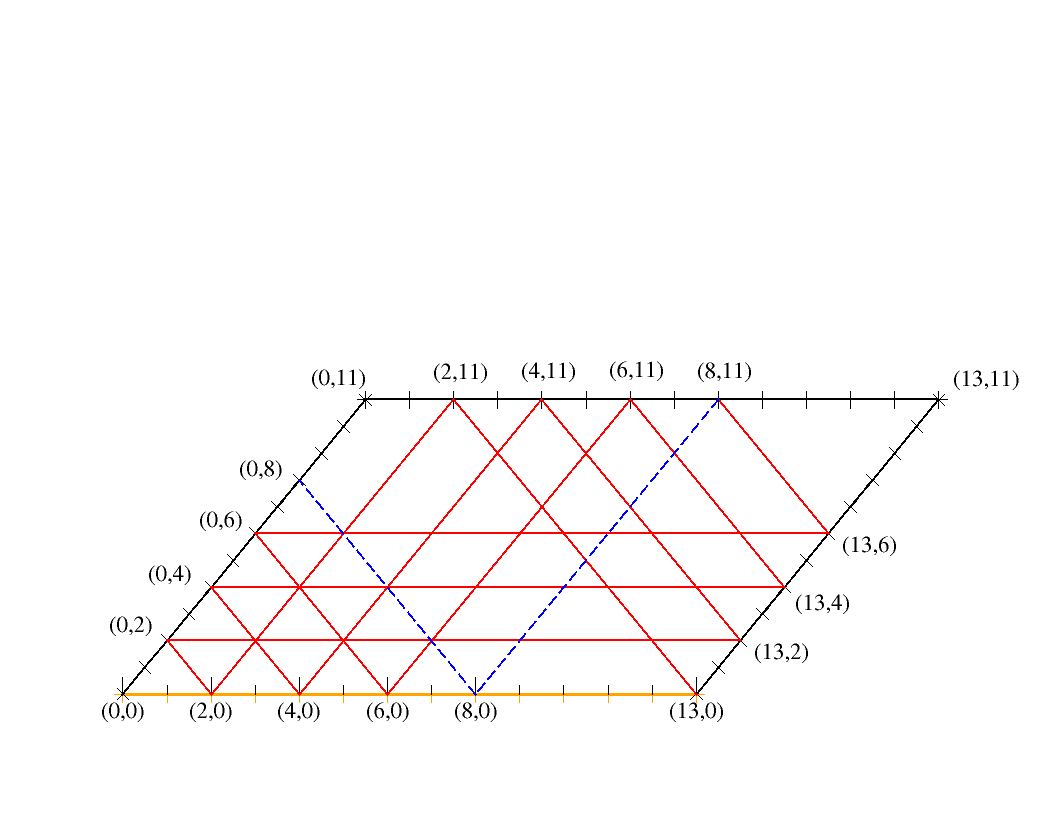
I had recently come across a geometric solution to these types of problems (Source: Mathologer on Youtube ). As can be seen in the figure, we can fix one of the axis above to represent filling the 13 liters container (here, the x-axis), whereas the 60 degrees line can represent filling the 11 liters container. Using simple collision rules, one can work out how to get 8 liters. To translate the figure in steps:

1) Fill the 13 liter container -- shown by the orange line

2) Pour 11 liters in the 11 liters container -- bounce to (2,11)

3) Empty the 11 liters -- bounce to (2,0)

4) Transfer the 2 liters to the 11 liters container -- bounce to (0,2)

5) Fill the 13 liter container -- bounce to (13,2)

6) Pour 9 liters in the 11 liters container -- bounce to (4,11)

7) Empty the 11 liters -- bounce to (4,0)

8) Transfer the 4 liters to the 11 liters container -- bounce to (0,4)

9) Fill the 13 liter container -- bounce to (13,4)

10) Pour 7 liters in the 11 liters container -- bounce to (6,11)

11) Empty the 11 liters -- bounce to (6,0)

12) Transfer the 6 liters to the 11 liters container -- bounce to (0,6)

13) Fill the 13 liter container -- bounce to (13,6)

14) Pour 5 liters in the 11 liters container -- bounce to (8,11) [ Solution already reached ]

15) Empty the 11 liters -- bounce to (8,0) [ Solution already reached ]

16) Transfer the 8 liters to the 11 liters container -- bounce to (0,8) [ Solution already reached ]

@Anant Dixit - very nice, and a very lucid explanation of it as well. Thanks for sharing this. It also provides a geometric interpretation of a solution $(4, -4)$ to the Diophantine equation $13 m + 11 n = 8 , m, n \in \mathbb{Z}$ . If arrowheads are added to each segment representing a step (so it is a directed graph), the 4 east-directed (horizontal) segments represent filling of the 13 L bottle and correspond to $m = +4$ while the 4 southwest-directed segments represent emptying of the 11 L bottle and correspond to $n=-4$ . And great pic!

Wesley Zumino - 3 years, 11 months ago

Arjen Vreugdenhil
Jul 11, 2017

Let $a > b$ be the sizes of the bottles.

At every stage of the process, one bottle is either completely full or completely empty. The other bottle contains an amount $x$ . Once we have an amount $x < b$ , it is easily transferred to the other bottle. We determine the amounts $x$ that can be generated.

Clearly, we can easily make the amounts $x = 0$ , $x = a$ , and $x = b$ by filling or emptying bottles.

There are four operations we may perform.

Suppose $x < a - b$ is in the large bottle. Fill the small bottle, transfer to the large. It now contains $x + b$ .
Suppose $x > b$ is in the large bottle. Empty the small bottle, pour from the large into the small. There is $x - b$ left.
Suppose $x > a - b$ is in the large bottle. Fill the small bottle, add to the large. The small bottle now contains $x - (a-b)$ .
Suppose any amount $x$ is in the small bottle. Fill the large bottle, add to the small. The large now contains $x + (a-b)$ .

Thus we can perform $x \mapsto x \pm b$ and $x \mapsto x \pm (a - b)$ , provided that $x$ remains between 0 and $a$ . Clearly the possible values satisfy $x = ma + nb$ with $m,n$ integers. This implies that $x | \text{gcd}(a,b)$ is a necessary condition. Is it sufficient? In principle we must perform $x \mapsto x \pm (a - b)$ precisely $|m|$ times, and $x \mapsto x \pm b$ , $|n + m|$ times. We only must be careful to do them in the correct order, so that $x$ remains between $0$ and $a$ .

In this problem, we have $a = 13$ , $b = 11$ , and want $x = 8$ . Since $8 = 4\cdot 2 = 4\cdot (13 - 11) = 4\cdot 13 - 4\cdot 11,$ we have $m = 4$ , $n = -4$ . This means that we need the operation $x \mapsto x + (a - b)$ four times, i.e. transfer $x$ to the small bottle, fill the big bottle, pour big into small--and repeat this four times.

Perfect explanation.

Kazem Sepehrinia - 3 years, 11 months ago

Very good explanation. Does this mean that for any two relatively prime bottle sizes a and b any integer value for x such that x<a can be obtained?

Jacob Lehmann Duke - 3 years, 11 months ago

I left that question unanswered... can you answer it? :)

Arjen Vreugdenhil - 3 years, 11 months ago

A Former Brilliant Member
Jul 11, 2017

Mathologer did a video on how to solve this type of question and the solution hi provided in his video How not to Die Hard with Math not only tells us if its possible or not but also tells the exact steps required to attain a given amount of water in a container.

Peter Newcomb
Jul 17, 2017

The difference between the two bottles volume is 2. Therefore each time you 1. fill the large bottle 2. pour the larger contents to the smaller 3. pour out the smaller 4. pour the larger contents to the smaller you end up with 2 more liters in the smaller bottle than you started with. Since 8 is divisible by 2, you repeat this 4 times to get 8 liters.

Ethan Hua
Jul 12, 2017

Step 1. Fill 13L container. Step 2. Empty the contents into 11L container. This leaves 2L remaining in the 13L container. Step 3. Empty out the 11L container into the sink. Step 4. Empty the 2L into the 11L container. Step 5. Refill the 13L. Step 6. Fill in 9L into the 11L container, leaving 4L left. Step 7. Do steps 1 - 6 until you have 8L.

It is easier to work it out on paper than drawing out diagrams. But, you can also do this in real life (if you have a 11 and 13L container) and you'd get the same results.

Mohammad Khaza
Jul 11, 2017

first of all, Fill the 13-liter bottle.

then , pour 11 liters into the 11-liter bottle. This leaves 2 liters of water remaining in the 13-liter bottle.

then, pour the 2 liters of water into the 11-liter bottle.

then, Fill up the 13-liter bottle again and pour 9 liters into the 11-liter bottle. This leaves 4 liters of water in the 13-liter bottle.

if we do this steps we will get 6 liter water and by doing this ,at last we will be able to get 8 liter waters.

Lily Boyle
Jul 11, 2017

1 - Fill the 13 liter container

2 - Pour its contents into the 11 liter container which leaves 2 liters in the other container (13 - 11)

3 - Empty the 11 liter container

4 - Pour the contents of the 13 liter container into the 11 liter container

The 11 liter container now holds 2 liters.

5 - Refill the 13 liter container

6 - Pour its contents into the 11 liter container which leaves 4 liters in the 13 liter container (13 - 11 + 2)

7 - Empty the 11 liter container into the sink

8 - Pour the contents of the 13 liter container into the 11 liter container

9 - Repeat all steps to obtain 6 liters by step 4 and 8 liters in the end.

Zach Cox
Jul 12, 2017

(STOPPER THE SINK)

(STEP-1) Fill the 13L

(STEP-2) Fill the 11L from the 13L

(STEP-3) Empty 2L remaining from 13L into sink

(STEP-4) Pour 11L into 13L

(DO STEPS) 1,2,3,4) four times gathering 2L, 4L, 6L, 8L in the sink.

Tom Chaplin
Jul 12, 2017

Fill the 13 Liters- 11 Liters (pour it into the 11 Liters) =2 Liters in the 13 Liter bottle pour this into the sink then repeat the first step 4 times (fill up the 13 Liter container, empty it into the 11. Pour it into the sink...)

Daniel The Marble Racer
Apr 8, 2020

1.Fill the 13-liter bottle.

2.Pour 11 liters into the 11-liter bottle. This leaves 2 liters of water remaining in the 13-liter bottle.

3.Empty the 11 liter bottle.

4.Pour the 2 liters of water into the 11-liter bottle.

5.Fill up the 13-liter bottle again and pour 9 liters into the 11-liter bottle. This leaves 4 liters of water in the 13-liter bottle.

Repeat this and you'll eventually you'll get 8L

Elisa Abarquez
Feb 17, 2018

13 and 11 are coprime, so there MUST be a solution. A solution can be found for any multiple of GCF of (a,b) units, where a,b are integers.

Francis Vanden Heede
Sep 15, 2017

Applying modulo operation.

Filling the 13 liter bottle by the 11 bottle results in a non-integer.

x*(11mod13)=8

11x=8

x=8/11

Filling the 11 bottle by the 13 bottle gives the right answer

x*(13mod11) = 8

2x=8

x =4

One need 4 steps of collecting the remainder of 2 liter in the way, described in the other answers, to obtain 8 liter.

Miksu Rankaviita
Sep 4, 2017

If you have the 11 liter bottle filled and the 13 liter bottle has x liters water, then if you pour water from the 11 liter bottle to the 13 liter bottle so that it gets full, $x-2$ liters will remain in the 11 liter bottle.

We can fill the 13 liter bottle and repeatedly fill the 11 liter bottle, pour some of it to the 13 liter bottle, empty the 13 liter bottle and finally pour the water in 11 liter bottle to the 13 liter bottle until there's only 1 liter left in the 13 liter bottle. We know this can be done because one action lowers the amount of water in the 13 liter bottle by two and $13-2-2-2-\cdots-2=1$ . Now when we pour 11 liters to the 13 liter bottle, it will have 12 liters inside. No we need to repeat the same action as before twice to get to 8 liters (because $12-2-2=8$ ).

Nicolai Hinsch
Aug 6, 2017

Make the 13-liter bottle full
Pour it into the 11-liter bottle and there are 2 liters remaining.
Empty the smaller bottle and give the 2 Liters into it

At this Point you can stop the process, because it is just adding rests. 11 and 13 are coprime numbers and it's possible to Keep the rest of both in one of this bottles. The residue classes of a multiple of two coprime numbers are leaving every possible rest before they reach a multiple of 13 (in this case it is of course not possible to reach an odd liter which is not 11 or 13, because it's just possible to subtract them and the difference is even)

Hansen Yang
Jul 21, 2017

13-11=2 2*4=8 litres. This is why there can be an exact 8 litres.

Matt P
Jul 13, 2017

If m>n, and m & n are mutually prime, any amount between m-n to m+n is possible. I wrote a c++ program years ago that writes out every step.

Size of 1st container: 11

Size of 2nd container: 13

Input target number = 8

(1) Start by filling the 13 container first. (2) Start by filling the 11 container first. (3) Silenty run both methods, and print only the most efficient. (TAKES LONGER) (4) Exit Program. Select an above method: 3

Filling the 13 first was more efficient by 17 steps.

(1)Fill the 13-gal 13/13 0/11 (2)Pour the 13-gal into the 11-gal (until full) 2/13 11/11 (3)Empty the 11-gal 2/13 0/11 (4)Transfer the 2-gals into the 11-gal container. 0/13 2/11 (5)Fill the 13-gal 13/13 2/11 (6)Pour the 13-gal into the 11-gal (until full) 4/13 11/11 (7)Empty the 11-gal 4/13 0/11 (8)Transfer the 4-gals into the 11-gal container. 0/13 4/11 (9)Fill the 13-gal 13/13 4/11 (10)Pour the 13-gal into the 11-gal (until full) 6/13 11/11 (11)Empty the 11-gal 6/13 0/11 (12)Transfer the 6-gals into the 11-gal container. 0/13 6/11 (13)Fill the 13-gal 13/13 6/11 (14)Pour the 13-gal into the 11-gal (until full) 8/13 11/11 (15)Empty the 11-gal 8/13 0/11 Press any key to continue . . .

Virgil Mepsted
Jul 12, 2017

Solution: realise it would be a stupid question if the answer was no and if would have been in die hard if it wasn't possible

42 of 100: Die Even Harder

19 solutions

0 pending reports