46 of 100: Nine Lives
At Step 101, how many cats will there be in the 9 th row?
Describe the pattern and be careful when you apply it!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
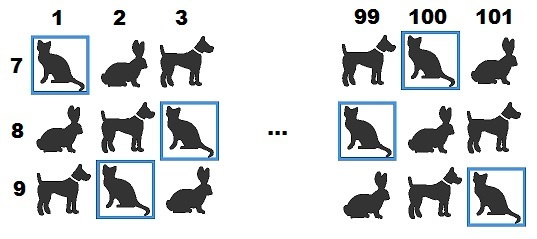
We note that every step increases one row and one column such that Step n has n rows and n columns. We also note that the pattern repeats every three columns to the left and every three rows down. Therefore, the 9th row is same as the 3rd row.
On the 9th row, if the column number is n , then n m o d 3 = ⎩ ⎪ ⎨ ⎪ ⎧ 0 1 2 ⟹ rabbit ⟹ dog ⟹ cat .
Therefore, the first cat is at n = 2 and the last is at n = 1 0 1 and the number of cats is 3 1 0 1 − 2 + 1 = 3 4 .
Wow, now I understand the solution a lot more than before. Thanks!
Step 101 is a 101 x 101 square. The patterns repeat after 3 rows. As we need 9th row, we can follow 3rd row. Cat starts at 2. Till 99 we get 99/3=33 equal no of animals. As it repeat after 3 squares, so the 100 th animal is dog, and 101th is cat. Thus total no of cat at 9th row of 101 step= 33+1=34
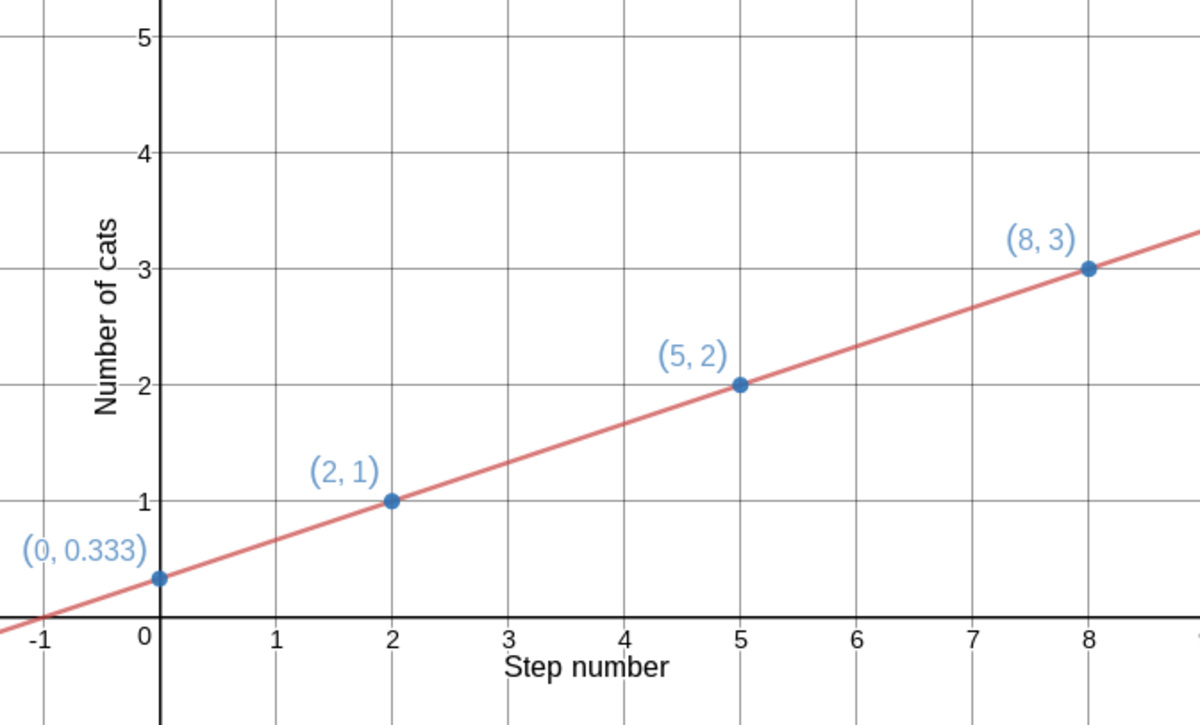
We know that the 9th row is the same as the 3rd row which is dog, cat, rabbit, dog, cat, rabbit.... Since step 2 has 1 cat or (2,1) and step 5 has 2 cats or (5,2) where (x,y)=(step, number of cats) we can set up a simple linear equation y=
3
1
x+
3
1
where we are gaining
3
1
cats every step which is the slope and the y-intercept is
3
1
which is how many cats there were at step 0.
Therefore if we are at step 101 which is x, we can say y=
3
1
(101)+
3
1
= 34
The 9th row will be the same as the 3rd row and the 6th row and so on. So the 9th row will start with a dog, then a cat followed by a rabbit. And then again dog, cat, rabbit. At step 101 there will be 34 dogs, 34 cats and 33 rabbits in the 9th row. The answer is 34.
wow good job can you explain how you got the answer?
Each row that is a multiple of three has a pattern of dog, cat, rabbit, dog, cat, rabbit, and so on. The matrix here at each step is always a square. So on the 101st step, there are 101 entries in each row.
For any row, we can predict the location of a dog, cat, or rabbit by looking at the remainder of division by 3. For every third row, a remainder of 1 corresponds to a dog, a 2 corresponds to a cat, and a 3 corresponds to a rabbit. If we divide 101 by 3, we get 33 with a remainder of 2. This means that there are 33 cats in the first 99 elements, then a dog, and then a cat. This leaves a total of 34 cats.
The ninth row will begin with a dog (every third row begins with dog). In 33 cycles of D,C,B there will be 33 cats and 99 animals total. The 100th animal is a dog, the 101st is a cat so add one more cat. That makes 34 cats. 🐱
The answer is the 9th Fibonacci number.
And if the question had asked, at step 104, how many cats will there be in the 9th row?
How did you get to this result?
Guessed from the pattern
Guess. Once drawn a diagram, you can figure out there is 34 cats.
- 9 is divisible by 3 so we know the row starts with a dog as the dog is the last element in the pattern.
- Knowing this, we now know that the second element will be the cat.
- To know how many cats are there, we can find out how many threes can go into 99 (the difference between 2 and 101 is 99)
- 99 divided by 3 is 33. Now we know that there are 33 cats.
- However, the 101st element is also a cat so we must add 1 to 33, leaving us with 34.
Notice along any row (or column), starting at row-0 (or column-0) you get the repeating sequence ("Cat","Rabbit","Dog").
So counting down, along column-0, to the 9th row you see it will start with "Dog".
This means that along the 9th row you have the repeating sequence ("Dog","Cat",Rabbit").
Counting along the 9th row you see there are 33 repetitions of that sequence that will get you to the 99th column (which will be "Rabbit").
Finally you notice that the 100th, and 101st columns of the 9th row must be "Dog", then "Cat".
So adding all that up you arrive at the arithmetic problem 33+1 which comes out to be 34
The cats are in the positions 2, 5, 8, 11, 14, ……… 3t < 100 t = 33 So the number of cats is 34 because in the 101 position there will be an extra cat.
Day 46. Step 4, 6 cats. 40-6= 34.
In step 101 there will be 101/3 = 33.6 of each animal, so there will be 34 of two animals and 33 of the third. Need to check if the cat is one of the first two positions.
The rows repeat every 3 positions, so row 9 will match row 3.
So, there are 34 dogs, 34 cats, 33 bunnies.
The pattern repeats itself after 3rd row and 3rd column. As such, the 9th row will be similar to 3rd and will start with a Dog (D), followed by Cat(C) and then Rabbit (R).
At the 101st step, each row/column will have 101characters.
As 101 = 3×33 + 2,.
The 9th row will consist of 33 sets of (DCR) and the remaining two characters will be Dog and Rabbit.
Total cats = 33 + 1= 34.
By looking at pictures 1 to 4 you can recognize a pattern:
First row: Cat, Rabbit, Dog
Second row:Rabbit, Dog,Cat
Third:Dog,Cat, Rabbit &... .
So the ninth row will start with Dog. 101 / 3 = 33 with the remainder of 2 and according to the pattern the Cat would be the second picture in row so, 33+1=34
| cat | rabbit | dog | cat | rabbit | dog | |
| rabbit | dog | cat | rabbit | dog | cat | |
| dog | cat | rabbit | dog | cat | rabbit | |
| cat | rabbit | dog | cat | rabbit | dog | |
| rabbit | dog | cat | rabbit | dog | cat | |
| dog | cat | rabbit | dog | cat | rabbit |
The first three rows repeat itself for the next three rows (i.e. first three rows start with cat, rabbit, dog, and next three rows start with cat, rabbit, dog).
Therefore, the 9th row at step 101 will start as the third row, which starts with dog.
Similar to the rows, the columns of the animals will alternate between cat, rabbit, and dog. Since the 9th row starts with dog, the second column is the cat and every three subsequent columns will contain a cat.
We can order the incidence of cats by column in the 9th row.
2 , 5 , 8 , 1 3 . . . 1 0 1 last term - 2 is divisible by three.
We just need to find the amount of terms in this sequence then.
The amount of terms in an arithmetic sequence with terms A1 through An and difference d is
d A n − A 1 + 1
The amount of cats in the 9th row at step 101 is
3 1 0 1 − 2 + 1 = 3 4
Edit: tl;dr. In short, you can figure out the progression of cats, which occurs every three columns. The cats start at the second column, so they will come from the second to the 101st column for each three columns. Then, using the last part of the solution, it is relatively simple to find the answer.
Here 9 is divisible by 3
Therefore the row will start with a dog
Then second element will be the first cat in the row
In 101 th step there will be 101 elements in the row
Therefore cat will be in position { 2,5,8,...,101}
It is an arithmetic progression
No of terms will be no of cats which is 34