47 of 100: A Simple Angle
A three-dimensional cube is shown above. What is the measure of ∠ A B C in degrees?
There are a lot of ways to solve this puzzle; look for a fast one, then try to find a second technique!
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
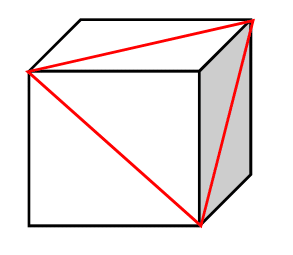 Adding the third face-diagonal completes an equilateral triangle. The angle is therefore
6
0
∘
.
Adding the third face-diagonal completes an equilateral triangle. The angle is therefore
6
0
∘
.
Nice picture. That's all there is to it. Solve on sight. Fastest, if not easiest so far. Three cacti?
nice way of thinking.i thought i would add a solution. but after watching this i understood that nobody would see my solution.
Log in to reply
You should still add it. Multiple solutions show that those don't think of the clever way, don't need to throw up their hands, that it is within their ability to find the answer. And who knows, maybe the way you thought of it will resonate with many others whose thinking ran along similar lines.
I found out through the same way you did.
The straightforward equilateral triangle argument is the best one, but here's another one just for fun.
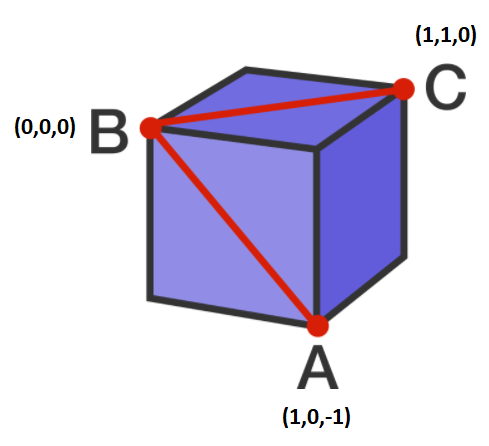
v 1 = ( 1 , 1 , 0 ) v 2 = ( 1 , 0 , − 1 )
Using a property of the vector dot product:
v 1 ⋅ v 2 = ∣ v 1 ∣ ∣ v 2 ∣ c o s θ 1 ( 1 ) + 1 ( 0 ) + 0 ( − 1 ) = 1 = 2 2 c o s θ c o s θ = 2 1 ⟹ θ = 6 0 ∘
Great solution!
If we connect A and C, that makes ABC an equilateral triangle with side length l 2 if l is the side length of the cube. And as obvious, each angle of an equilateral triangle measures 6 0 ∘
Thorns abound... And the problem of yesterday was "Thorns about". I feel like today's problem is 0% difficulty and yesterday's was one of the most difficult challenges.
LaTex: Let an orthonormal coordinate system defined by : ( B , B C ′ = ı , A A ′ = ȷ , B ′ B = k )
LaTex: B A = B C ′ + B B ′ = x i − x k
LaTex: B C = B C ′ + A A ′ = x i + x j
LaTex: Norm of the vectors : ∥ B A ∥ = ∥ B C ∥ = 2 ( x 2 + x 2 ) = 2 ( 2 x 2 ) = 2 2 x
LaTex: scalar product : B A . B C = x 2
LaTex: Let’s use the formular of cosine : cos ( ∠ ( A B C ) ) = ∥ B A ∥ . ∥ B C ∥ B A . B C = 2 2 x . 2 2 x x 2 = 2 1
LaTex: cos ( ∠ ( A B C ) ) = 2 1 ⟺ ∠ ( A B C ) = ± 3 π = 6 0 °
LaTex: Thus the angle is part of a regular or equilateral triangle inscribed in the cube.
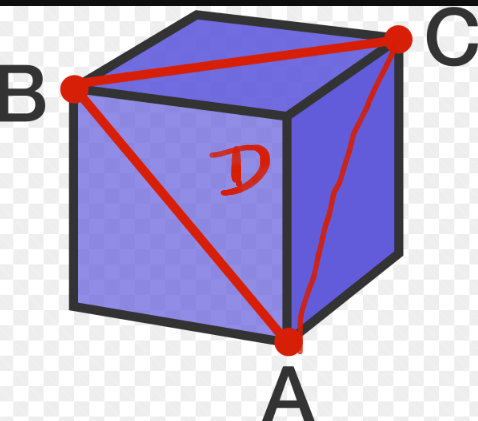
Here if we cut the pyramidal shape ABCD we can see the base is ABC
AB=BC=CA
SO ABC is an equilateral triangle.
So the angle is 60 degree
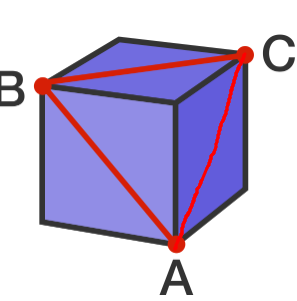
we can rotate this and the cube will remain the same, and the traingle will appear the same but its sides are rotated. hence by symmetry all sides are equal and hence all angles are 6 0 ∘
Guys, Don't need to think much. The Distances AB=BC=AC. That's because we're talking about a cube. Hence its an equilateral triangle. Angle is 60.
You can prove it using origami

Alternatively, the diagonals of a face are sqrt(2) All the edges are diagonals all the edges are the same equilateral triangle 60 degrees
AB = BC = CA = 2 * a [ Diagonal of square ]
where a = side of cube
Hence, triangle is equilateral, so ∠ A B C = 6 0 ∘
The answer is 60 because, when you connect A and C you have a triangle. If you imagine that you cut through flush with all three lines then you get an equilateral triangle. So, because all the angles in an equilateral triangle are equal and all the angles in a triangle add up to 180, the answer must be 60
Draw the third line A C . By symmetry, we know that each angle in the resultant triangle A B C must be equal, so ∠ A B C must be 60 degrees.
Cut cross a section, It will show 60 degrees.
If we want to find the angle formed by ∠ A B C , we must first consider the fact that the angle itself exists on a plane, since there is always one plane containing three points. Ignoring the line segments, we can create our plane and find that the plane creates an equilateral triangle cross section of the cube.

Since we already know the cross section is an equilateral triangle, we can now easily find the measurement of angle ∠ A B C by dividing its interior angle sum 180º by 3.
If we mean the angle in the equilateral triangle ABC the angle is obviously 60 degrees, But if the dihedral angle, is wanted, what would it be. I mean the pyramid whose apex angle is <ABC? I researched it and found a formula but I do not know how to use it, do you have an easy way to find it?
Draw in line segment AC and the triangle ABC is equiangular. Thus, the measure of angle ABC is 60 (180/3).
Just add A and C to find triangle ABC. ABC is indeed an equilateral triangle as AB,BC,CA are all diagonals of a face (square shaped) of cube. so, each and every angle is 60 degrees. <ABC = 60
If we place the origin at the bottom left corner of the cube. The coordinates are as follows : A = (0,1,0) B = (1,0,0) C = (1,1,1) Vector CB = (1,1,1) - (1,0,0) = (0,1,1) Vector AB = (0,1,0) - (1,0,0) = (-1,1,0) The dot product of the 2 vectors (CB.AB) is 0 -1 + 1 1 + 1 0 = 1 Now cos(ABC) = CB.AB / [ l(CB) * l(AB)] = 1/[sqrt(2) sqrt(2)] = 1/2 Therefore since ABC is acute and since cos(60) = 1/2, ABC = 60
The fastest way I found to approach this was to create a triangle. If we draw a line for A to C, we notice that triangle ABC is equilateral. We know this because sides AB, BC, and CA are all diagonals of sides of the cubes and are therefore equal. Since triangle ABC is equilateral, all of its interior angles must equal 60 degrees, and <ABC is an interior angle of triangle ABC. Therefore, <ABC must equal 60 degrees.
Looking at the image above, connecting point A to point C forms a triangle - specifically an equilateral triangle since each side is
s
2
. Therefore, angle ABC is
60
degrees.