5 of 100: A Sum of Shapes
Each shape in this puzzle represents a numerical value. The number next to each row or column represents the sum of all of the values in that row or column.
Can the center of the grid be filled in with one of the three shapes? If so, which one?
While it is possible to solve for the value of each symbol, there is a quick and clever way to solve this problem without finding the specific value of any of the shapes.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
49 solutions
The argument "we cannot put a circle there, as 14 on the center row isn't divisible by 3" seems invalid.
The shapes represent numerical values, not just integers.
You just made an assumption (wrong) that some shape will work. It could be None also.
In your proccess of eliminating choices, you failed to eliminate the option: "None of the shapes work".
Your second statement, that a star will contradict that the top row = 12, has no evidence to support this claim. It is also true that your third statement suffers from the same lack of evidence. You basically said "a square is correct because it is".
letting x =square, y= circle, z = star, ? =t, the equations are satisfied by t=4, y=5,x=4,z=3, so it is not necessary fot ? to be one of the other three; ed gray
- 14/3 = ?. Remember that the numerical values have to be EXACT, not approximate.
- The top row (square + star + circle) = 12 is already given and therefore if we put a star in the middle, it contradicts the given row's answer (take a look at the central column).
- If none of the shapes actually worked, then why do we have S+S+C = 13 and C+C+S = 14 as solution? Remember this: 2(even) + odd = odd. 2(odd) + even = even. This is an intuition-based solution and not computational.
Log in to reply
14/3 is exact... I am not sure what the problem is here.
Nothing in the problem statement limits the shapes to positive integers. 14/3 is a numerical value. 𝛑 is also a numerical value. It happens that solving the problem via linear equations gives integers as a value, but assuming each shape is an integer because it doesn't take the form ◼︎.▲▲◼︎● is a bad assumption.
Just multiply by 2 the first row and then subtract the third row,
2 STAR + 2 SQUARE + 2 CIRCLE - 2 STAR - SQUARE = 2*(12) - 10
2*CIRCLE + SQUARE = 14
so we need the square in the second row!
We can also try with the first and third column
Really pretty solution! Thanks for sharing.
So straight forward solution :D . Thanks for sharing with us.
Very elegant solution.
Each shape appears two times in the total sum. If you let x represent the square, y circle, z star, and w the unknown shape, then from the total sum we get 2 w + 4 x + 6 y + 6 z = ( 1 0 + 1 4 ) + ( 1 1 + 1 3 ) + ( 1 2 + 1 2 ) = 6 × 1 2 ⟹ 6 2 w + 4 x + y + z = 1 2 And from first row we get x + y + z = 1 2 . Put this in the above equation 6 2 w + 4 x + ( 1 2 − x ) = 1 2 ⟹ 2 w + 4 x = 6 x ⟹ w = x Thus the unknown shape can be square.
@Kazem Sepehrinia please have a look at EGMO 2012 . i have posted my solution.
3 symbols of each=the square
In column 3, there is 2 stars and a circle and their sum is odd. So, the circle is definitely odd.
In row 3, there is 2 stars and a square and their sum is even. So, the square is even.
In column 1, there is a star, a square and a circle and their sum is even. Again we know that the circle is odd and the square is even. So, the star is definitely odd.
In row 2, there is 2 circles and their sum is even. So, in the "?" mark, there will definitely be an even. As only square is even, so it will be square.
How does this logic eliminate "none" as a possible solution?
Log in to reply
I think that because this logic makes a solution correct, it eliminates "none" as a possible solution. "None" can't be a solution if a solution is correct.
The problem never says the shapes have to be integers. So you didn't eliminate the possibility that circle is the answer. Also, you did not eliminate the possibility that the answer is "none".
We can write an equation for each row and column in which every figure is represented by a variable, for example: asigning x to square, y to circle, z to star and w to the center space we have the following system:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x + y + z = 1 2 2 y + w = 1 4 y + w + x = 1 3 2 z + y = 1 1 2 z + x = 1 0
then solving the system of equations we obtain:
x = 4 , w = 4 , y = 5 , z = 3
We have the same value for the center of the grid, corresponding to the value of x that represents the square, thus the figure that satisfies all the row and column sums is the square.
I knew the answer and I was scrolling down but instead star option clicked for no reason....I have answered everything correct so far....this is so bad
Log in to reply
Maybe the mobile version would be safer for you. In mobile, you have to confirm your answer so it isn't as likely mistakes like this would happen.
When we go from column 3 to column 1 we substitute a star by a square and the result is 1 higher.
So, if we substitute both stars for 2 squares, the result will be 2 higher that 11. Which makes it 13.
Therefor, 2 squares amd a circle is 13, which makes the center piece a square.
This solution used only 2 columns. Is there a better way to do it?
The left column and the right column are almost the same, except that the left column has a square on top where the right column has a star. This gives the left column a sum 1 greater than the right column. Therefore, square is 1 greater than star.
The left column consists of a square, a circle, and a star. The middle column consists of a square, a circle, and the mystery number -- the only difference is that the middle column has the mystery number instead of a star. The middle column is 1 greater than the left column. Therefore, the mystery number is 1 greater than star.
Since the mystery number is 1 greater than star, and square is 1 greater than star, the mystery number must be square.
I like this solution because it arrives at an answer without actually finding the numeric values of any of the shapes.
I swear I typed mine up before seeing yours :-)
Uh... simplest solution EVER. If you insert star, he wins the tic-tac-toe game. If you insert circle, he wins. But if you insert SQUARE, no one wins.
I let x = square, y = circle, z =srar, t = ? and solving the equations, z=3, x = 4, y = 5, and t = 4. So the ? =square. I must have hit the wrong choice inadvertenly. I notice that once in a while, an answer is chosen for you before you have a chance to answer. Edwin gray
Consider three column from left to right be C 1 , C 2 , C 3 .
We can see that C 1 has 1 bigger than C 3 ,we can know that square is 1 bigger than star by cancellation.
So, as the same, C 2 is 1 bigger than C 1 , we know that the question mark must be a icon that 1 bigger than star also by cancellation, so the answer is S q u a r e .
in the second row circle is not possible.because 14 is not divisible by 3.
in the third row there is 2 star. so,square must be in an even number.so,we can get the values of circle=5, square=4, star=3.
so,5+4+5=14. so, square is the answer.
nice solution.
Comparing columns 1 and 3, replacing the square with a star makes the sum change from 12 to 11 (down by 1). Therefore: square = star + 1. Comparing rows 1 and 3, replacing the circle with a star makes the sum change from 12 to 10 (down by 2). Therefore: circle = star + 2. You can write the equation for the top row as (star + 1) + (star + 2) + star = 12 and solve to get star = 3, which means square = 4 and circle = 5. Then just substitute into either row 2 or column 2 to get the center shape must be 4, which is a square.
i realized that there are 3 stars, 3 circles, and 2 squares. i thought, obviously, you would have to have 3 squares for the pattern to be true. that way, you don't have to do the calculation.
This isn't a sudoku.
Lol same, everyone is being so mathematical. I legit didn't even look at the numbers. We took the easy solution, great minds think alike my friend ❤️
Here's what I think is the simplest explanation yet. Since row one is 2 more than row three, and the only difference between those rows is one circle vs. one star, then a circle must be 2 more than a star. Now row two is 4 more than row three, and since each circle is two more than each star, we have accounted for the 4 difference. The middle shape must be the same, i.e. square.
there are already 3 stars and 3 circles, so why not have 3 squares
x+y+z=12 2y+c=14 2z+x=10 multiply eq1 by 2 and subtract from (eq2+eq3) x=c
From the third row, squares have to be even (2*star is even, so a square is even), from the 3rd column, Circles must be odd by the same logic, and from the first row, knowing squares are even and circles are odd, a star has to be odd as well. Thus, in order to make Circle + Square + ? odd, you have to add an even number, a square
well for me it was very easy so here is what i did there were already 3 circles so it was definitely not that there were already 3 stars so it was definitely not that as well and there were only 2 squares so i thought it was that and i was correct.
From the first row and the third row, we can derive that
Circle = star + 2
Insert in third column to get 3 • star + 2 = 11 Thus star = 9/3 = 3 Thus circle = 3 + 2 = 5. Now, 5 + x + 5 = 14, iff x = 4.
Use any row or column with a swuare to conclude that square = 4. For example top row: Square + circle + star = Square + 5 + 3 = Swuare + 8 = 12, so square = 4.
There were 3 stars and 3 circles, but only 2 squares. So I chose square
since there are three of each shapes and the only remaining is the square.
From the first and last column you can see square is greater than star by 1. So you can substitute square= star+1 in the equation.
We are looking for a sum amounting to 13.
- The sum of the first column differs from the last column by 1, hence square must be larger than a star by 1.
- Hence replacing the star by a square in the first row will increase the sum by 1 (to 13).
- Hence square+square+circle=13; which is the solution.
- From first column and 3rd column we know Square is one more than Star
- Then from third row, we know star is 3 and square is 4
- Using that info in column one OR column 3 we know Circle is 5
- Square+?+Circle=4+?+5=13 and
- Circle+?+Circle=5+?+5=14
- We have ?=4=Square satisfy the puzzle.
On the grid all the shapes except the square appears three times by using common sense the square is the most obvious choice
Looking at the spaces that are on the outlying part of the square there is a one shape difference in all of them. I set up a systems of equations using this and the sums of the respective columns.
Sq+C+St=12 St+C+St=11 When you subtract you find out Sq-St=1
Next: St+C+St=11 St+Sq+St=10 Subtracting gives us C-Sq=1
Now we know that C>Sq and Sq>St by one each, making them consecutive numbers. The only values that satisfy all of the equations known are 3,4,5 respectively. Just by plugging in you will find that
St=3, Sq=4 and C=5
Therefore to satisfy all our equations the symbol in the middle must be a square
The sum of the the first row is the average of the sum of the second and third row. Hence the ? must be a square.
Its quite obvious. I just looked at the grid and saw that the square must be 4, the circle 5, and the star 3, so the square made the grid complete. I also transformed the shapes to variables and made it a system of equations with 4 variables and solved to check my answer.
s = s t a r , c = c i r c l e , q = s q u a r e , w = u n k n o w n
2 s + q = 1 0
2 s + c = 1 1
Therefore c = q + 1
s + c + q = 1 2
2 s + c = 1 1
Therefore q = s + 1
Therefore c = s + 2
Therefore s + ( s + 1 ) + ( s + 2 ) = 1 2
Therefore s = 3 , q = 4 , c = 5
2 c + w = 1 4
Therefore w = 4
Therefore w = q
Comparing the second column to the first, the center has to be 1 more than a star. Comparing the third column to the first, we can see that the square must be 1 more than a star. So: square.
2Stars + Circle = 11
2Stars + square = 10
Square = 10 - 2stars
Circle = 11 - 2stars
Using row 1:
(10 - 2stars) + (11 - 2Stars) + 1Star = 12
21 - 4stars + 1star = 12 -3stars = -9
star = -9/-3
star = 3
2(3) + square = 10 therefore square = 4
2(3) + circle = 11 therefore circle = 5
So algebraically the answer is square in the middle.
I worked it out like so:
- [Star + Circle + Star = 11] - For two stars and a circle to equal 11 one of the shapes must be odd. Since there are two stars it can't be that (2 odds can't make an even), therefore circle is odd.
- [Star + square + star = 10] - If star is odd or even it doesn't matter here, the sums of both will be even so square must be even.
- [Square + circle + star = 12] - If we know a circle is odd and square is even then to get an even result (12) star must also be odd.
Using these deductions we take [circle + ? + circle = 14] :
- Circle is odd and therefore 3 of them can't equal an even. (14 isn't divisible by 3 either)
- Star is odd but given that there are two circles which we know to be odd the total cannot be even.
- Square is even and two odd circles make an even so square is feasible.
lol everyone is getting so mathematical when it's really down to simple logic. There are 3 STARS and 3 CIRCLES but only 2 SQUARES. So the missing one is a SQUARE because then you would have 3 of each shape.
But this answer is just coincidentally right, you could have a 3 by 3 square with 4 stars, 3 circles, and 2 squares, for example. It's not really a solution, the fact that in the end there are three of each is unrelated to the problem at hand.
The simplest way is: Other than square all are 3 in quantity Therefore a square must come😅
Why does there have to be 3 of each?
I honestly just used logic. There were 3 circles, and 3 stars, but only 2 squares.
This doesn't imply the solution is square.
Star=3, Square=4, Circle=5. I just used process of elimination, even though there are probably faster ways to do it. I figured out that circle has to be one greater than square because star circle star equals 11 and star square star equals 10. From there I just started plugging in values of star to find what worked and then determined which value would work in the final spot.
3 circles, 3 stars so there should be 3 squares. simple
Why would there have to be 3 of each?
Here's the trick: Star+Star+Circle=11 (an odd number)-this means that the stars could be even or odd, and the circle must be odd. Star+Star+Square=10 (an even number)-this means (again) that the stars could be even or odd, and the square must be even. Square+Circle+Star=12 (an even number)-we know that the circle is odd, and the square is even, meaning that the star must be odd in order to get an even result.
Now turn the attention to the problem at hand: Circle+Circle+(?)=14 The circles are both odd. As we know, ODD+ODD=EVEN, so we need to add an even number to get 14. The square is the only even number, so it must be the symbol that goes in the middle.
Numerically, 2 × C 1 = C 2 + C 3 ; 2 × R 1 = R 2 + R 3 .
In symbols, 2 ( ∘ + ⋆ + □ ) = 2 ∘ + 2 ⋆ + □ + ? ; 2 ( ∘ + ⋆ + □ ) = 2 ∘ + 2 ⋆ + □ + ? .
The obvious solution is ? = □ .
Is it the only solution? Comparing C 1 , C 3 shows that ⋆ = □ ; comparing C 3 , R 3 shows that ∘ = □ .
Besides the obvious missing shape - a Quadrilateral,
here is an algebraic solution:
S=Star; C=Circle; Q=Quadrilateral; X=The shape in the center.
Q C S 12
C X C 14
S Q S 10
Q+C+S=12
Q+S+S=10 By subtracting we get C-S=2
C+X+C=14
S+Q+S=10 By subtracting we get X-Q=0
So X=Q. The missing shape in the center is a Quadrilateral.
Since 2 stars + square = 10, which is even, the square is even. Since 2 stars + circle = 11, circle is odd. Since star + circle + square = 12, star is odd. Since 2 circle + ? = 14, ? must be even. Hence ? must be a square since it's the only even one.
(\color{Blue}{Row
1} - \color{Red}{Column
3} = \color(Yellow}{Square} - \color{Red}{Star} = 12-11 = 1)
\color{#D61F06}{Column_2} - \color{#D61F06}{Column_1} = \color{#CEBB00}{*?*} - \color(Red}{Star} = 13-12 = 1
=
>
∗
?
∗
=
S
q
u
a
r
e
.
Please any moderator, make that correct. I couldn't.
for the total number of rows, each shape appears 3 times except the square wich appear 2 times, and the case is similar for the total number of columns. So we can guess that the square is the missed shape and then prove it trivially.
Why can we guess the square is the missed shape?
I just first looked at 11 and by instinct, I said star was 5. That means the square must be 0 (for 10) And if you add the 12, (5+0+green circle) the green circle must be 7
If you read number 14, 7 + 7 + ?, so ? must equal 0 and we all know what 0 is... the square!
Look at the right column. There are 2 stars and 1 circle whose sum is 11. That means circle is odd number.
Now look at the 3rd row. There are 2 stars and 1 square with the sum of 10. That means square is an even number.
Now look at the 1st row. There are 1 star, 1 circle and 1 square with the sum of 12. That means star is an odd number since odd+odd+even=even
Then, at the middle row, you have 2 circle which sum is an even number. Thats mean you can only put square to make the sum even.
PS. I'm sorry for my grammar, I'm bad at it
Hi friends! To find the solution to this problem we will first of all add up the horizontal rows figures and put that quantity equal to the numerical value.We will end up something like this :
2(Square) + 3(Star) + 3(Circle) + ? = 12+14+10= 36. ............eq.(1)
We come to know from the first vertical line that Square+Star+Circle= 12 "Or" it can be written as 3{Star +Circle+Square}= 12X3 =36.......... eq(2)
On equating the left sides of both eq(1) and eq(2) , we get ? = Square
Hope you liked the solution. Have a Brilliant day!!
We see that a square, circle, and star combined are equal to 12. The next two rows or columns have 1 square, 2 circles, 2 stars, and the unknown shape that sum to 24. Since we know the first fact, it would be logical that the square makes the second equation true by multiplying the first equation by two and equating squares, circles, and stars. Therefore, the shape must be a square.

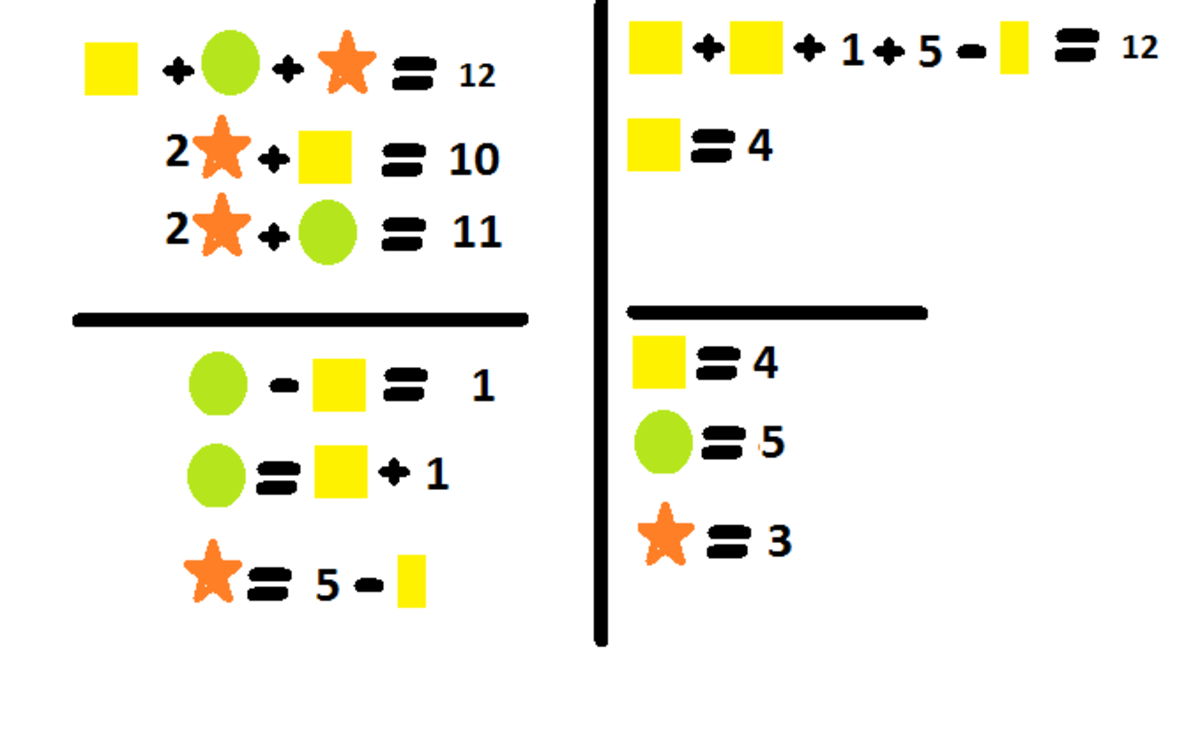
Obviously, we cannot put a circle there, as 14 on the center row isn't divisible by 3. The star can't be placed there either, because that will contradict the fact that a star, a circle, and a square is equal to 12. When a square is put, the statement in center-center line becomes true. Therefore, the shape for the middle part of the square is a SQUARE.