50 of 100: Lumière des Lunes
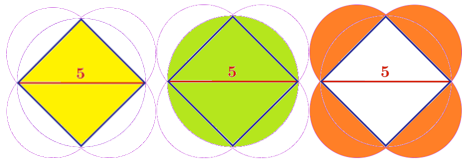
The four sides of a square are used as diameters to define four overlapping, congruent circles. Then, a larger circle is drawn so that it passes through all four corners of the square. The length of the square's diagonal is 5.
What is the total area of the regions shaded purple?
Hint: In one approach to solving this puzzle, you start by finding the length of one side of the square.
The answer is 12.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
What am I missing? Brilliant says that the answer is 5, but to me the answer is very clearly 12.5. Since the diameter of the blue circle is the diagonal of the square, and the diameter of a purple circle is the side of the same square, the diameter of the blue circle is bigger than the diameter of the purple circles by a factor of the square root of two, and the area of the blue circle is bigger than the area of the purple circles by a factor of two. The total area of the figure is clearly four purple semicircles = two purple circles + the area of the square. The area of the purple regions is clearly the area of the entire figure minus the area of the blue circle. Since the area of the blue circle is equal to the area of two purple circles, the area of the purple regions is clearly equal to the area of the square. The area of the square is clearly 25/2 = 12.5. This is just like your alternative solution, except that we don't even need to involve pi! What is up with the answer Brilliant gives?
Log in to reply
12.5 is the answer
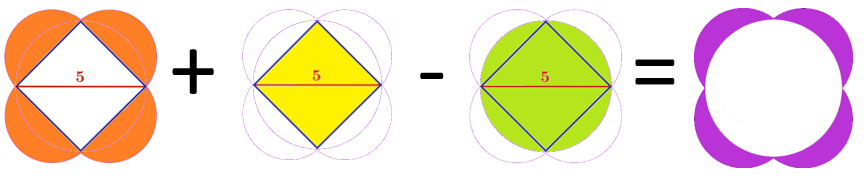
Area of purple region = Area of 4 small-semi-circles + area of square - area of large circle
Side of square = 5/sqrt(2).
Radius of each small semi-circle = 5/(2*sqrt(2)
Area of each small semi-circle = pi * (5/(2*sqrt(2))^2 / 2 (We divide by 2 because it is a semi-circle)
Area of 4 small semi-circles = 4 (pi 25/8)/2 = 2 (pi 25/8) = 25*pi/4
Radius of large circle = 5/2
Area of large circle = pi (5/2)^2 =25 pi/4
Thus area of purple region = area of square = (5/sqrt(2))^2 = 25/2 = 12.5
which is the answer i got initially but got the response as incorrect
I don't know! There is a mistake, problem should be edited!
I too arrive at the conclusion that answer is 12.5
It seems most got the answer 12.5. I think Brilliant should edit this problem.
I got 12.5 too.
Yes - I get 12.5 too. Since th comments are well-argued, and unanimous, clearly the given solution needs editing. Please!
I also got 12.5
12.5 is the correct answer
The answer is indeed 12.5. Apparently 8% of people made the same mistake as the person who set the problem - not very brilliant! It would save a lot of face if they actually bothered to correct the error rather than letting it stand :-(
as other comments, answer is clearly 12.5.
Yes the answer is 12.5 only
I really liked this lemma!
NOTE THANKS TO COMMENTS FROM OTHERS I HAVE CORRECTED MY SOLUTION:
This problem can be solved using composite areas.
In order to do this we first need the length of a side of the square which can either be found using a 45-45-90 special right triangle or pythagorean theorem. Here is the work using pythagorean theorem.
a 2 + b 2 = c 2
s 2 + s 2 = 5 2
2 s 2 = 5 2
s 2 = 2 5 2
s = 2 5 2
s = 2 5
Then we need to find the areas of the following shapes
1.The squares area is
A = ( 2 5 ) 2
A = 2 2 5
A = 1 2 . 5
- The large central circle
A = π ( 2 5 ) 2
A = 4 2 5 π
- The area of the four semicircles
A = 4 2 π ( 2 2 5 ) 2
A = 2 π ( 2 2 5 ) 2
A = 2 π ( 8 2 5 )
A = 4 2 5 π
The area of the purple regions is then found by finding the sum area of the 4 semicircles and the square and subtracting the large circle
4 2 5 π + 1 2 . 5 - 4 2 5 π = 1 2 . 5
You are using diameter value as radius. Luckily it got canceled and you are getting the results. Need to modify the circle area calculation with radius values.
Log in to reply
Thank you. Since I got the answer I did not go back and check my math. I have made corrections per your comment.
Your calculations for the areas of the circles is off, but you've made the same scaling error in both cases so their difference is still zero.
Log in to reply
Thanks for your comment. The error has been corrected.
This math is so bad, I don't know how you put some numbers together to get 12.5
Log in to reply
Math has been corrected. As per the first comment I had accidentally used diameter for radius.
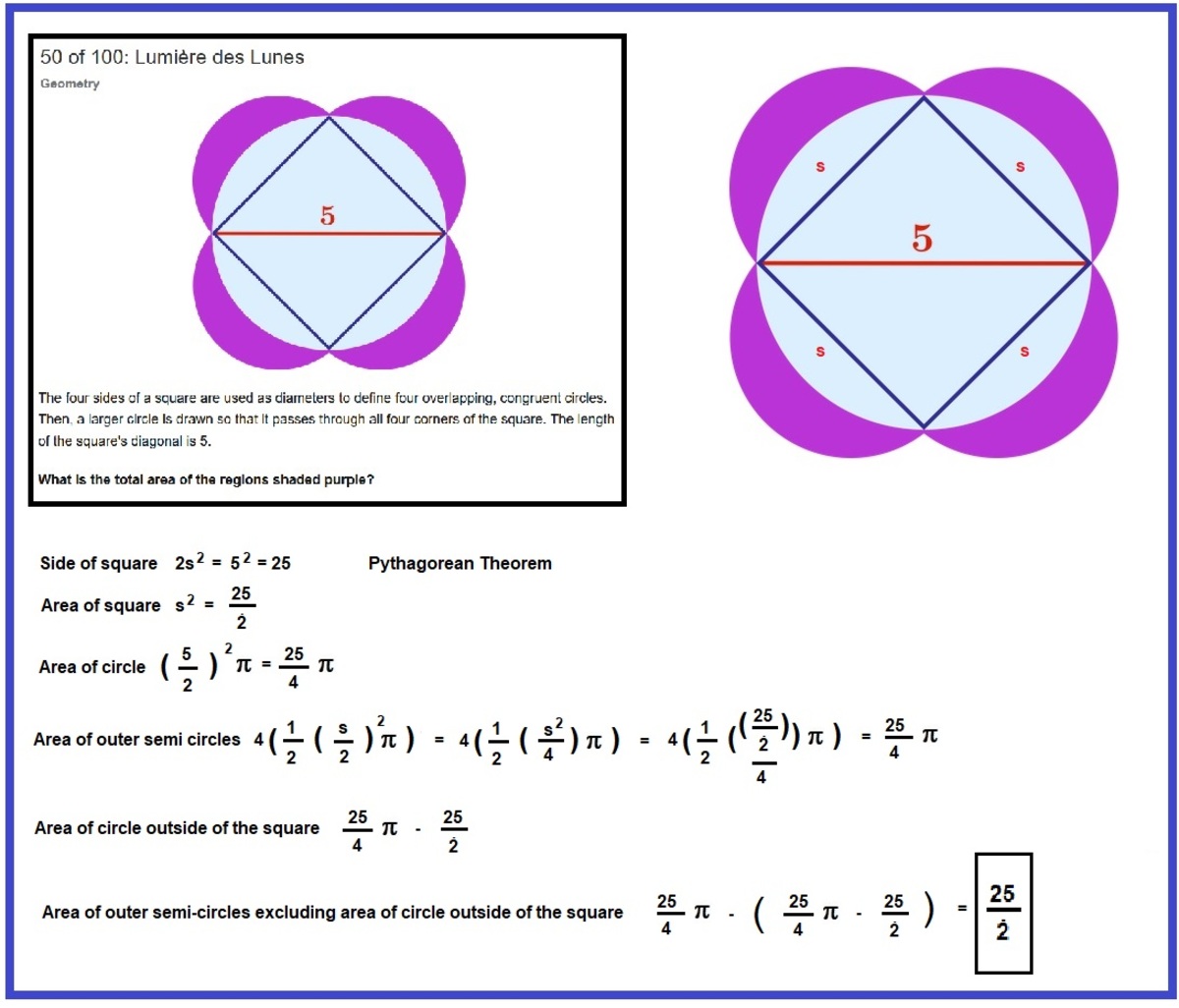
Here's a slightly altered version of the diagram:
I started by seeing this as a square with four semi-circles around it. We can work out the area of the whole thing by finding the area of 2 circles and adding it to the area of the square.
Then we need to subtract the bigger circle (shown here in yellow), to leave the area we want:
Rather than use 5 as the diagonal of the square, I called half of that diagonal
x
Putting in the other diagonal of the square gave me four right-angled triangles. The hypotenuse of these is useful, because it is the side of the square and also the diameter of the semi-circles.
The area of the square is 2 x 2
The radius of each semi-circle is 2 2 x and this gives the total area of the four semicircles as π x 2
So, the area of the whole thing is 2 x 2 + π x 2 and we need to subtract the area of the big yellow circle, which is π x 2
This leads to the wonderful result that the area of the four lunes is the same as the area of the square, namely 2 x 2
In this particular case x = 2 . 5 , and this gives the area of the purple lunes as 12.5 square units.
Great explanation! Simple enough, I took the same approach.
How could the area of the large circle, which circumscribes the square be 25(3.1415...)? The radius is 2.5, if the diameter is 5, thus the area is (2.25)^2(3.1415...), which is 6.25(3.1415...)=19.63.
Log in to reply
Hi Steven, Sorry - I don't understand what you mean here. I have defined the radius of that circle to be x, so I didn't use 25 pi. Hope that clears things up.
On reflection, I think you might have meant to post this on Matthew's answer!
Log in to reply
Yes, it was supposed to be a response to Matthew's answer.
Brilliant way of looking at the diagram - I couldn't understand some of the other solutions till I looked at yours.
 Lune of Hippocrates. Yellow area = blue area. In the given problem, the purple area = the area of the square = 12.5
Lune of Hippocrates. Yellow area = blue area. In the given problem, the purple area = the area of the square = 12.5
If you take one-quarter of the figure, you have a triangle (A), a segment (B), and a crescent (C). The area of the triangle is easy. Now (A+B) is one-fourth of the area of the large circle and (B+C) is one-half of the area of the small circle. Both of these numbers are easily determined. So you can now write an equation for the area of the crescent as C = (B+C) - ((A+B) - A). The answer, oddly enough, is A. So 4 x C = 4 x A, which happens to be the area of the square in the middle of the figure.
One additional point........the answer does not involve pi even though the perimeter of the crescent is made up of two intersecting circles. In other words: "No pi for you!" As far as I know, this is a unique characteristic of this type of crescent. Does anyone know whether there are other "circular" shapes that share this oddity.
In the above diagram, label the areas as shown. By Pythagoras the sidelength of the square is 2 5 √ 2 (with the denominator rationalised). Therefore that is also the diameter of all of the 4 small circles, making their radius 4 5 √ 2 . As the area of a semicircle is 2 1 of πr², the area a + e = 1 6 2 5 π .
Therefore, the area a + b + c + d + e + f + g + h = 1 6 2 5 π x 4 = 4 2 5 π as this includes 4 lots of a + e.
The area of the square (labelled i) is 2 5 √ 2 x 2 5 √ 2 = 4 5 0 = 12.5
The pale blue circle has diameter 5 (given) so the area is π x 2.5² = 4 2 5 π . In the notation of areas on the diagram: e + f + g + h + i = 4 2 5 π
This gives us 3 equations: a + b + c + d + e + f + g + h = 4 2 5 π
e + f + g + h + i = 4 2 5 π
i = 12.5
Equating the first two gives us that a + b + c + d + e + f + g + h = e + f + g + h + i, or a + b + c + d = i. However, since i = 12.5, a + b + c + d = 12.5 also and from the diagram, the purple areas are labelled a, b, c & d.
Hence, the total area of the regions shaded purple is 12.5
4 π ( 4 5 √ 2 )² − π ( 2 5 )² + ( 2 5 √ 2 )² − 2 π ( 4 5 √ 2 )² = 1 2 . 5
Area of the 4 small circles - Area of the big circle - Area of the small curved cross left
 The long, stupid way to do it, by me
The long, stupid way to do it, by me
| Calculation | Explanation |
| I have 4 semi circles with radius = s q r t ( 2 ) 2 . 5 | we get this from a^2 + b^2 = c^2 where a = b and c = 2.5 |
| The semi circles have an area of 4 * 2 1 * PI * s q r t ( 2 ) 2 . 5 ^2 = 6.25PI | semi circle = 2 1 * PI * r^2 |
| segment area = 2 1 * r^2 * ( 2 P I - sin( 2 P I )) = 2 1 * 6.25 * ( 2 P I - 1) | each segment is 4 1 circle so they have an angle of 2 P I radians |
| area of segment = 2 1 * r^2 * (angle-sine(angle)), where angle is radians | |
| total segment area = 6.25PI - 12.5 | With 4 segments, total area = 4 * 1/2 * 6.25 * (PI/2 - 1) |
| 6.25PI - 6.25PI + 12.5 area = 12.5 | subtracting the segments from the semi circles |
Consider the blue region above the square, then its area A is:
A = pi(5/2)^2 – 25/2 = 25pi/4 – 25/2
Since the side square a satisfies:
a^2 = 25/2
Then the pink area A’ is:
A’ = (2pi)(a/2)^2 – A = 25pi/4 – A = 25/2 = 12.5.
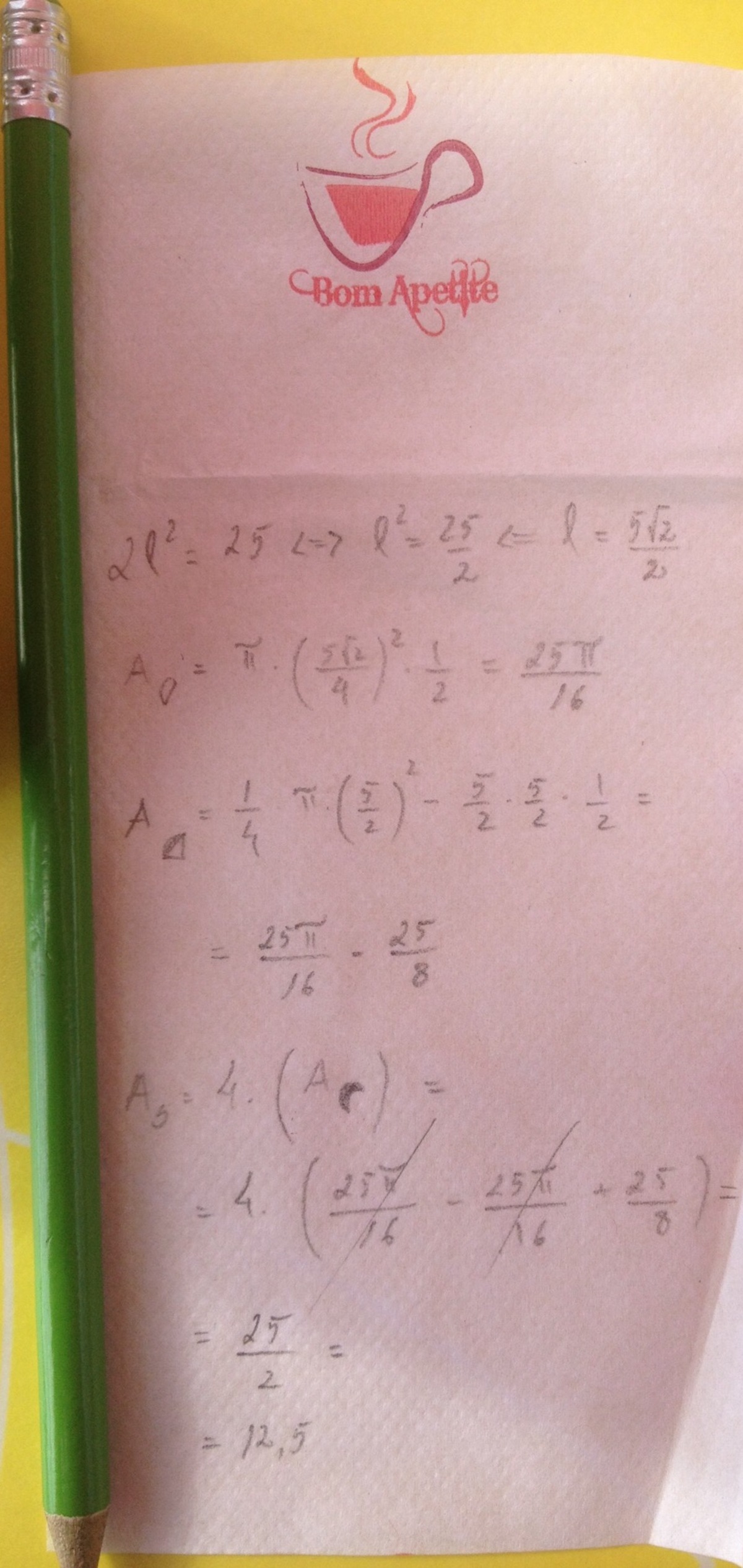
Consider the following more general figure: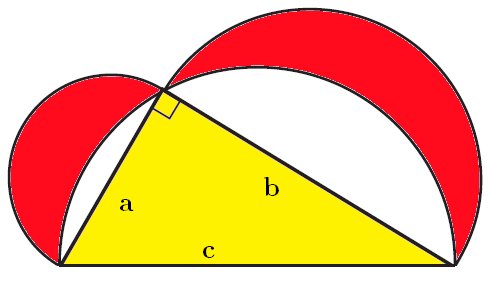 Lemma:
Area of red region is equal to area of yellow region.
Lemma:
Area of red region is equal to area of yellow region.
Proof: Area of red crescents = area of right triangle + 2 1 area of small circle + 2 1 area of medium circle - 2 1 area of large circle = area of right triangle + 2 1 4 π ( = 0 a 2 + b 2 − c 2 ) = area of right triangle.
Thus we have: purple area = square = ( 5 / 2 ) 2 = 1 2 . 5 .
Alternatively:
One purple area= 4 1 square + 2 1 small circle - 4 1 large circle
Total purple area = square + 2 small circle - large circle = 2 5 / 2 + 2 π ( 2 5 / 8 ) − π ( 5 / 2 ) 2 = 1 2 . 5