51 of 100: Some Simple Fractions
1 1 1 1 1 1 1 0 , 2 2 2 3 2 2 2 1 , 3 3 3 4 3 3 3 1
Which is largest?
This can be quickly and cleverly solved without a calculator and without explicitly calculating the value of each fraction. Make an argument, don't just use your intuition!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
Rewrite problem as: which is largest: 1 − 1 1 1 1 1 , 1 − 2 2 2 3 2 , or 1 − 3 3 3 4 3 . This is clearly equivalent to: which is smallest, 1 1 1 1 1 , 2 2 2 3 2 , or 3 3 3 4 3 ? Since 1 1 1 1 1 = 2 2 2 2 2 > 2 2 2 3 2 , the first is clearly not the smallest. That leaves us with the task of comparing 2 2 2 3 2 and 3 3 3 4 3 . Quick cross-multiplication (compare 3 ∗ 2 2 2 3 with 2 ∗ 3 3 3 4 ) shows that 3 3 3 4 3 is larger, leaving 2 2 2 3 2 as the smallest. Thus 2 2 2 3 2 2 2 1 is the largest of the three original fractions.
I used the same method, to compare the three a/aaab fractions I used theyr inverses, so I easily calculated the results by hand and take the biggest one.
That's how I did it, made it easier to compare fractions with smaller numerators.
b a < b + c a + c given that b > a
1 1 1 1 1 1 1 0 = 2 2 2 2 2 2 2 0 < 2 2 2 3 2 2 2 1 = 6 6 6 9 6 6 6 3 > 6 6 6 8 6 6 6 2 = 3 3 3 4 3 3 3 1
1 1 1 1 1 1 1 0 2 2 2 3 2 2 2 1 3 3 3 4 3 3 3 1 = 1 − 1 1 1 1 1 = 1 − 2 2 2 3 2 = 1 − 1 1 1 1 2 1 1 = 1 − 3 3 3 4 3 = 1 − 1 1 1 1 3 1 1
Since 1 1 1 1 2 1 1 < 1 1 1 1 3 1 1 < 1 1 1 1 1 , ⟹ 2 2 2 3 2 2 2 1 > 3 3 3 4 3 3 3 1 > 1 1 1 1 1 1 1 0 .
This is nice :)
best solution
Nice & simple
That's the trick I used.
Each of these is close to but not greater than one, so you may rephrase the question as "Which has the smallest difference from 1?" Subtracting and making a common numerator gives:
1- 1 1 1 1 1 1 1 0 = 1 1 1 1 1 = 6 6 6 6 6
1- 2 2 2 3 2 2 2 1 = 2 2 2 3 2 = 6 6 6 9 6
1- 3 3 3 4 3 3 3 1 = 3 3 3 4 3 = 6 6 6 8 6
Since the numerators are all the same, the largest denominator is the smallest number, and therefore 2 2 2 3 2 2 2 1 is the correct answer to the problem
Your solution and the solution presented by Chew-Seong Cheong are the cleanest explanations of this task that I've seen so far. I got this problem wrong due to a rash conclusion that I made as a result of my analysis. However, in the spirit of this problem I feel that a comprehensive analysis should consider the following: given that N/D = 1110/1111 , then 2221/2223 = (2N + 1)/(2D + 1) and 3331/3334 = (3N + 1)/(3D + 1) . Note the condition that D > N for this task. One can easily show that (kN + 1)/(kD + 1) > N/D when k > 1 . In the following calculations, the position of left side and right side are maintained.
-
Compare (kN + 1)/(kD + 1) to N/D by multiplying both sides by D•(kD + 1).
-
Compare (kND + D) to (kND + N) by subtracting kND from both sides.
-
Compare D to N with the result that D > N. Therefore (kN + 1)/(kD + 1) > N/D .
Both 2221/2223 and 3331/3334 are larger than 1110/1111 , which leaves the issue which of these two fractions is largest 2221/2223 or 3331/3334?
-
Compare (aN + 1)/(aD + 1) to (bN + 1)/(bD + 1) with the assumption that b > a > 1. Multiply both sides by (aD + 1)•(bD + 1).
-
Compare (abND + aN + bD + 1) to (abND + aD + bN + 1) by subtracting (abND + 1) from both sides.
-
Compare (aN + bD) to (aD + bN) by subtracting bN and aN from both sides.
-
Compare b(D - N) to a(D - N) by dividing both sides by (D - N).
-
Compare b to a with the result that b > a. Therefore (aN + 1)/(aD + 1) > (bN + 1)/(bD + 1).
This final result means 2221/2223 > 3331/3334 .
if x = 1 1 1 0
A = 1 1 1 1 1 1 1 0 = x + 1 x
B = 2 2 2 3 2 2 2 1 = 2 x + 3 2 x + 1
C = 3 3 3 4 3 3 3 1 = 3 x + 4 3 x + 1
Cross multiply the A and B, you end up with
2 x 2 + 3 x < 2 x 2 + 3 x + 1
in the numerator, so B is larger.
Now cross multiply B and C, which gives you
6 x 2 + 1 1 x + 4 > 6 x 2 + 1 1 x + 3
in the numerator, so B or 2 2 2 3 2 2 2 1 is larger.
1 1 1 1 1 1 1 0 = 1 − 1 1 1 1 1 2 2 2 3 2 2 2 1 = 1 − 2 2 2 3 2 = 1 − 2 × 2 2 2 3 1 = 1 − 2 × 1 1 1 1 × 2 + 1 1 = 1 − 2 × 2 × ( 1 1 1 1 + 2 1 ) 1 = 1 − 1 1 1 1 + 2 1 1 3 3 3 4 3 3 3 1 = 1 − 3 3 3 4 3 = 1 − 3 × 3 3 3 4 1 = 1 − 3 × 1 1 1 1 × 3 + 1 1 = 1 − 3 × 3 × ( 1 1 1 1 + 3 1 ) 1 = 1 − 1 1 1 1 + 3 1 1
The largest fraction is the one in which the least quantity is subtracted from 1.
So, the answer is 2 2 2 3 2 2 2 1 ,
In fact this fraction has the same numerator of the others and a greater denominator.
Great choice!
if we multiply these 3 fractions with big integers, the difference between numerator and denominator will be seen. and the fraction with the largest numerator or denominator will be close to 1 than other numbers. so, the answer will be = 2 2 2 3 2 2 2 1
again, their is another way, if we subtract these all fractions from 1 (as they all are less than 1), than these fractions will be, 1 1 1 1 1 < 2 2 2 3 2 > 3 3 3 4 3
need clear explanation.
Your inequalities are pointing in the wrong directions.
LaTex: Let : A = 1 1 1 1
LaTex: Let : e = A A − 1 , f = 2 A + 1 2 A − 1 , g = 3 A + 1 3 A − 2
LaTex: Let’s suppose : e < f
LaTex: e < f ⟺ A A − 1 < 2 A + 1 2 A − 1 ⟺ ( A − 1 ) ( 2 A + 1 ) < A ( 2 A − 1 ) ⟺ − 1 < 0 ⇒ True
LaTex: Let’s suppose : e < g
LaTex: e < g ⟺ A A − 1 < 3 A + 1 3 A − 2 ⟺ ( A − 1 ) ( 3 A + 1 ) < A ( 3 A − 2 ) ⟺ − 1 < 0 ⇒ True
LaTex: Let’s suppose : f < g
LaTex: f < g ⟺ 2 A + 1 2 A − 1 < 3 A + 1 3 A − 2 ⟺ ( 2 A − 1 ) ( 3 A + 1 ) < ( 2 A + 1 ) ( 3 A − 2 ) ⟺ − 1 < − 2 ⇒ False
LaTex: Thus : f > g
LaTeX: Finally ( e < f ) , ( e < g ) and ( f > g ) ⇒ e < g < f ⇒ f = 2 A + 1 2 A − 1 = 2 2 2 3 2 2 2 1
LaTeX: That is to say : "$f$" is the largest number between the 3
LaTex Another way to find the largest number :
LaTex: Let : a = 1 1 1 0
LaTex: Let : A ( a ) = a + 1 1 a + 0 , B ( a ) = a + 2 3 a + 2 1 , C ( a ) = a + 3 4 a + 3 1
LaTex: l c m ( 1 ; 2 ; 3 ) = 6 then let’s multiply every numerator and denominator :
LaTex: Let : A ( a ) = 6 a + 6 6 a + 0 , B ( a ) = 6 a + 9 6 a + 3 , C ( a ) = 6 a + 8 6 a + 2
LaTex: [ a → 0 lim A ( a ) = 6 0 = 0 ] , [ a → 0 lim B ( a ) = 9 3 = 3 1 ≈ 0 . 3 3 ] , [ a → 0 lim C ( a ) = 8 2 = 4 1 = 0 . 2 5 ]
LaTex: We can now sort the 3 numbers : A ( a ) < C ( a ) < B ( a ) ⟺ 0 < 4 1 < 3 1
LaTeX: Thus, the largest number between the 3 is : B ( a ) = a + 2 3 a + 2 1 = 2 2 2 3 2 2 2 1
For positive values, if b a > d c then a d > b c .
Let x = 1 1 1 0 , then the fractions are:
1 1 1 1 1 1 1 0 = x + 1 x , 2 2 2 3 2 2 2 1 = 2 x + 3 2 x + 1 , and 3 3 3 4 3 3 3 1 = 3 x + 4 3 x + 1
For the first two,
x ( 2 x + 3 ) < ( 2 x + 1 ) ( x + 1 )
2 x 2 + 3 x < 2 x 2 + 3 x + 1
0 < 1
So the second is greater than the first. Then for the second vs. the third,
( 2 x + 1 ) ( 3 x + 4 ) > ( 3 x + 1 ) ( 2 x + 3 )
6 x 2 + 1 1 x + 4 > 6 x 2 + 1 1 x + 3
4 > 3
So the second is the highest.
Just do some changes 1-1/1111 1-2/2223 3-3/3334 2/2223=1/2223/2=1/1111.5<1/1111
So by this u get ur answer morons
Lol "topper forever" xD
All these fractions are clearly a little less than 1. Write them initially as "1 minus something":
1 1 1 1 1 1 1 0 =1- 1 1 1 1 1
2 2 2 3 2 2 2 1 =1- 2 2 2 3 2
3 3 3 4 3 3 3 1 =1- 3 3 3 4 3
Now look at the amounts that have been deducted from 1; the smallest deduction will lead to the largest original fraction.
Make the numerators the same; lowest common multiple is 6 ...
1 1 1 1 1 is 6 6 6 6 6 , 2 2 2 3 2 is 6 6 6 9 6 , and 3 3 3 4 3 is 6 6 6 8 6
Looking at the denominators, 6669 is the largest, so 6 6 6 9 6 is the smallest deduction from 1, so we can conclude that 2 2 2 3 2 2 2 1 was the largest of the original fractions.
a/(a+1)< (2a+1)/(2a+3)>(3a+1)/(3a+4)
1 1 1 1 1 1 1 0 - 2 2 2 3 2 2 2 1 = 1 1 1 1 ∗ 2 2 2 3 1 1 1 0 ∗ 2 2 2 3 − 1 1 1 1 ∗ 2 2 2 1 = 1 1 1 1 ∗ 2 2 2 3 1 1 1 0 ∗ ( 2 2 2 3 − 2 2 2 1 ) − 2 2 2 1 = 1 1 1 1 ∗ 2 2 2 3 − 1 <0; 2 2 2 3 2 2 2 1 > 1 1 1 1 1 1 1 0
2 2 2 3 2 2 2 1 - 3 3 3 4 3 3 3 1 = 2 2 2 3 ∗ 3 3 3 4 2 2 2 1 ∗ 3 3 3 4 − 2 2 2 3 ∗ 3 3 3 1 = 2 2 2 3 ∗ 3 3 3 4 2 2 2 1 ∗ ( 3 3 3 4 − 3 3 3 1 ) − 6 6 6 2 = 2 2 2 3 ∗ 3 3 3 4 1 >0; 2 2 2 3 2 2 2 1 > 3 3 3 4 3 3 3 1
The largest is 2 2 2 3 2 2 2 1 .
Let 1110 = a. The numbers now are a/(a+1), (2a+1)/(2a+3), and (3a+1)/3a+4). Now let a=1, so now the fractions are 1/2, 3/5, and 4/7. The second, 3/5, is the largest.
1110/1111 = 1 – 1/1111
2221/2223 = 1 – 2/2223 = 1 – 1/1111.5
3331/3334 = 1 – 3/3334 = 1 – 1/1111.3333......
Since obviously,
1/1111 > 1/1111.33…. > 1/1111.5
So,
1110/1111 < 3331/3334 < 2221/2223.
Therefore 2221/2223 is largest.
Let a = 1 1 1 0 . Then the three fractions become a + 1 a , 2 a + 3 2 a + 1 and 3 a + 4 3 a + 1 . We can systematically cross multiply the three pairs: A and B ; A and C ; B and C and compare the result.
A and B : ( a ) ( 2 a + 3 ) ? ( a + 1 ) ( 2 a + 1 ) ⇒ ( 2 a ) ( a ) + 3 a ? ( 2 a ) ( a ) + a + 2 a + 1 . Since 0 < 1 , A < B .
B and C : ( 2 a + 1 ) ( 3 a + 4 ) ? ( 2 a + 3 ) ( 3 a + 1 ) ⇒ ( 2 a ) ( 3 a ) + 8 a + 3 a + 4 ? ( 2 a ) ( 3 a ) + 2 a + 9 a + 3 . Since 4 > 3 , B > C .
Since B is greater than both A and C , we can conclude B is the greatest out of the three fractions.
Notice how we don't need to compare the third pair A and C , because the information doesn't add any new information to the conclusions we made from the pairs A and B ; and B and C .
Isn't this why God invented calculators/spreadsheets. And yes - if you put the 3 fractions into Excel, the answers look the same. All you have to do is widen the cells. (Sometimes, with this sort of problem, you have to increase the decimal places - Home:General:decimals) Do you take your carpets outside to beat the dust out cos vacuum cleaners are nasty modern mechanical inventions?
Yes, you could definitely use a calculator, but I believe that calculators should be used only after students understand the mathematical concepts behind the numbers. I never said that calculators are supposed to be banned - they have to be used wisely so that students don't neglect the mathematical foundations before moving on to higher-level maths.
In this case, learning different techniques such as cross multiplying, subtracting from 1 , differences between numerator and denominator and so on help students build up a rich foundation to move further into mathematics. If you just plug the numbers into a calculator, you will never be able to generalise these sorts of problems into algebra. These are all based on symbols, which a regular scientific calculator can't divide.

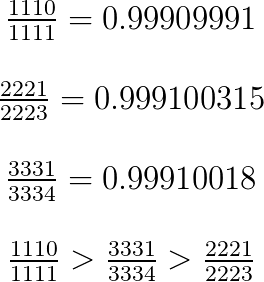
1 1 1 1 1 1 1 0 = 6 6 6 6 6 6 6 0
2 2 2 3 2 2 2 1 = 6 6 6 9 6 6 6 3
3 3 3 4 3 3 3 1 = 6 6 6 8 6 6 6 2
For each fraction, the difference between numerator and denominator is the same (6), so the fraction with the largest numerator or denominator will be the closest to 1, hence the answer is 2 2 2 3 2 2 2 1 .