52 of 100: Solve It Like Mondrian

Notice that $ab=120$ and $(16-b)(18-a)=24$ . Put first in second to get $(16-b)(18-\frac{120}{b})=24$ . This is a quadratic for $b$ and it has two solutions: $b=\frac{40}{3}$ and $b=8$ . On the other hand $\frac{b}{d}=\frac{40}{25}=\frac{8}{5}$ . Thus, $d=\frac58 b$ .

For $b=\frac{40}{3}$ we get $d=\frac58 \times \frac{40}{3}=\frac{25}{3}$ , which in turn gives $b+d=\frac{65}{3}>16$ . This is impossible.

$b=8$ gives $d=\frac58 \times 8=5$ and $c=16-8-5=3$ . Finally $x=\frac{48}{b} \times c=\boxed{18}$ .

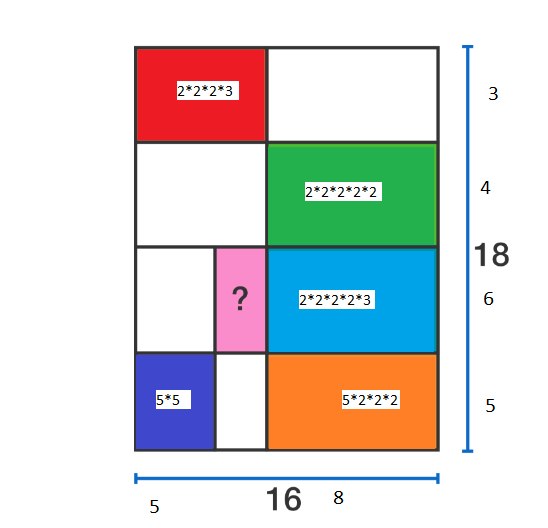
25 can only be expressed as 5*5, so the height and base of the dark blue rectangle are both 5.

Breaking down each other rectangle into their prime factors allows you to work out their side lengths.

The orange rectangle has a base of 8 and the dark blue has a base of 5.

5 + 8 + X = 16 (where X is the pink rectangle's base)

X = 3

The pink rectangle has a height of 6, so the area (6*3) is 18.

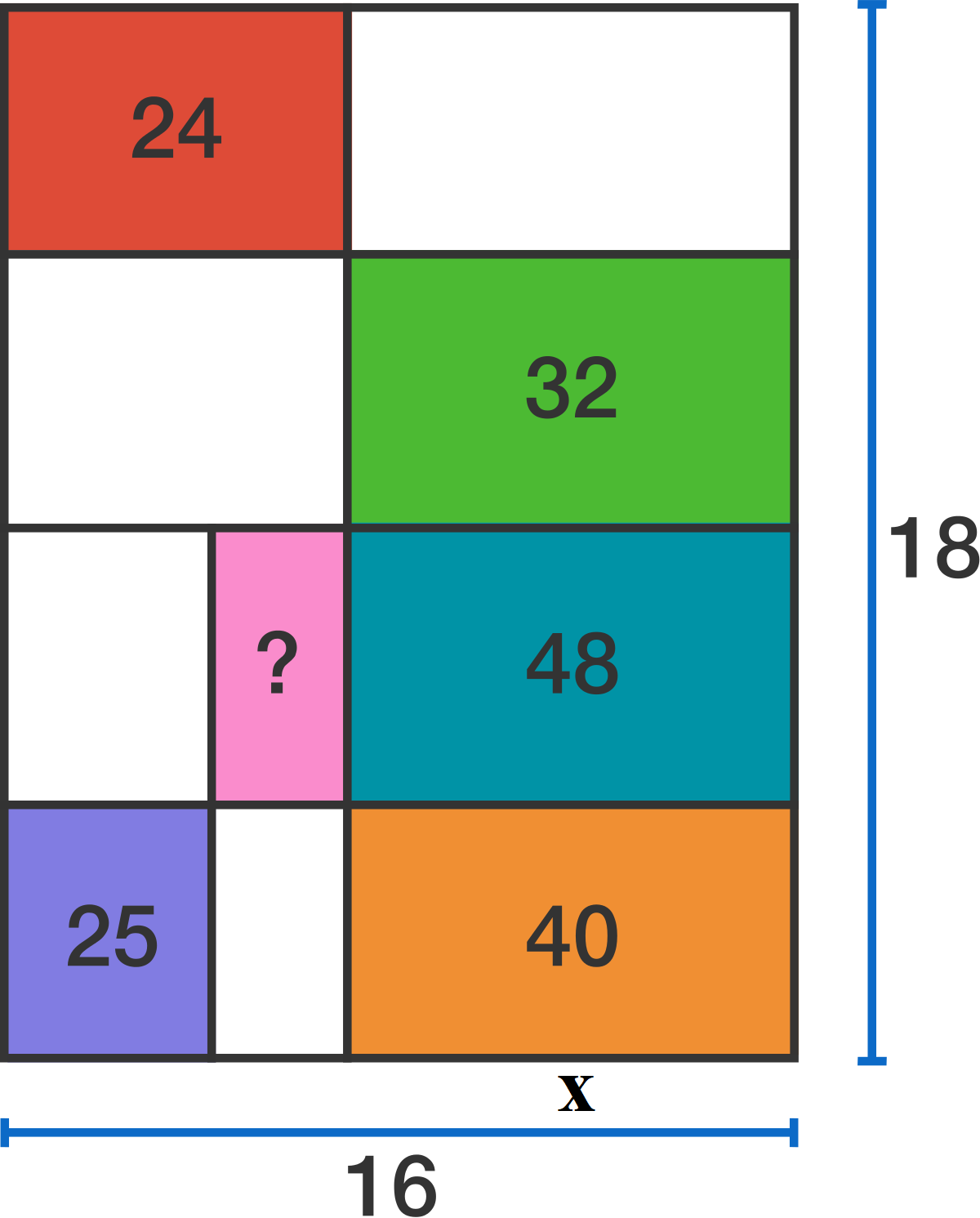
Let $x$ be the area of the pink rectangle, and let $y$ be the area of the upper-right rectangle.

Then $\frac{y}{24+y} = \frac{120+y}{288}$ , which leads to a quadratic equation with two solutions: $y=24$ or $y=120$ . We can toss out 120, since then the total of $y$ and the areas of the given rectangles would be 289, which is larger than the entire outer rectangle.

So $y = 24$ , which lets us calculate the heights of the vertical subdivision as 5, 6, 4, and 3 (totalling 18), from bottom to top.

It also shows us that the main vertical dividing line splits the outer rectangle into two identical halves.

So now we have $\frac{x}{6} = \frac{40-25}{5} = 3$ , so $x = \boxed{18}$ .

the length will be 6 and the width will be 3................[for the pink rectangle]

so, the area of the pink rectangle will be = $6\times 3$ = $18$ ...................[as the biggest common factor of 40 and 48 is 8 and also the other side of the rectangle with the area of 48 is 6. so, it should be like this:length =6 and width=16-(8+5) =16-13=3]

Extend the vertical line so 3 rectangles on the left are split, then by proportionality with the known rectangles on the right, two more rectangle areas can be filled in:

   24          ?

 24   ?       32

 30   ?       48

 25   ?       40

Collapse that to:

    24            A

 75    B         120

The total area is 16*18 = 288=A+B+24+75+120, so A+B = 69

       24           A

  75    (69-A)     120

For any rectangle subdivided into 4 smaller rectangles, the product of the diagonal areas is equal to the product of the off-diagonal areas (proof left to the reader), so

$24*120 = (75 + 69 - A)A = (144-A)A = 144A - A^2$

$A^2 - 144A + 24*120=0$

$(A-24)(A-120)=0$

A=120 is not a valid solution (because then B=69-A would be negative), so A=24.

Since the top two rectangles are the same area (and the same height), they are the same width, each half of 16, namely 8. Thus all the blocks on the right are width 8. The 48 block is 8x6, so the pink box is also height 6. The 40 box is 8x5, so the purple is height 5 and thus 5x5, so the white box under pink has width 3, and so does the pink.

Pink box is height 6, width 3 ==> area 18.

LaTex: $\large \text {To find some of the values, let's use the gcd :}$

LaTex: $\large \gcd(a\times d, a\times e, a\times f) = \boxed {a = 2^3 =8} \;\text{so, } \; a\times f = 2^3\times5 \iff \boxed{f=5}$

LaTex: $\large \text {Thus : } \; f\times c_1 = 5^2 \iff \boxed{c_1 = 5} = f$

LaTex: $\large \text {Thus :}\; 16 = a + c \iff \boxed{c=2^3=8} = a \; \text {and} \; \boxed{c - c_1= 3}$

LaTex: $\large a\times e = 2^4\times 3 \iff a\times e = 2^3\times 6 \iff \boxed {e=6}$

LaTex: $\large \text {Finally, the pink area is : } \;\color{#E81990}{ (c-c_1) \times e} \color{#333333}{ \iff } \color{#D61F06}{3 \times 6 = \boxed {18}}$

Let the area of pink rectangle be x. The area of blank rectangle on left of pink is (48/40)(25) = 30. Let the whole area of rectangle (30+x) = A.
Then in terms of A, the area of rectangles above and below it are (2/3)A {=(32/48)A} and (5/6)A {=(40/48)A} respectively. The area of top blank rectangle in terms of A is (48/A)(24).
So the total area of the figure can be written as (5/6)A +A+(2/3)A+24+(48×24/A)+120 = 16×18.
This simplifies to,
5A^2 - 288A + 48×48 = 0,
Or, (A - 48)(5A - 48) = 0,
Or, A = 30 + x = 48 or 48/5,
Or, x = 18 or -102/5,
Since x is not negative, so x = 18.

Try every possible answer. I have started from 15 then picked 18 as second try and succeed.

Assuming integer divisions, the bottom left must be 5x5 and the Orange must be 8x5. It is then trivial to see that the pink is 3x6 giving an area of 18. But, will this always hold?

Let's label the width of the bottom left rectangle as $x$ . Then its height is $\frac{25}{x}$ .

This means that the orange rectangle is also $\frac{25}{x}$ tall and thus $\frac{8x}{5}$ long.

The 48 rectangle must be $\frac{30}{x}$ tall.

So the pink rectangle is $16-\frac{13x}{5}$ wide by $\frac{30}{x}$ tall.

The area is $\frac{480}{x}-78$ .

But, what is $x$ ?

Following up, we see that the green rectangle must be $\frac{20}{x}$ tall. Leaving $18-\frac{75}{x}$ for the height of the red rectangle.

Now the area of the red rectangle fits the equation:

$(18-\frac{75}{x})(16-\frac{8x}{5})=24$

This simplifies to:

$3x^2-40x+125=0$

$(3x-25)(x-5)=0$

$x=\frac{25}{3}$ or $x=5$

But, if $x=\frac{25}{3}$

$\frac{480}{\frac{25}{3}}-78=-20.4$

This is clearly not possibly, so the only answer is when $x=5$ and The area is $\frac{480}{5}-78$ =18.

The biggest common factor of 40 and 48 is 8, therefore the other side of the rectangle with the area of 48 is 6.
There is only 1 way of dividing 25 into 2 numbers that suits the base of the triangle and that is 5 * 5
16 - ( 8 + 5 ) = 3
3 * 6 = 18

So 3x6=18

Let's say the pink area is x. By setting ratios equal, e.g we see that the area left of it must be $\frac{25×48}{40}=30$ , and the area below it $\frac{40x}{48}= \frac{5}{6}x$ . Expressing all four white areas in terms of x, we find 30, $\frac{5}{6}x$ , $20+\frac{2}{3}x$ and $\frac{1152}{30+x}$

Now add up the total area:

$24+\frac{1152}{30+x}+ 20+\frac{2}{3}x+32+30+x+48+25+ \frac{5}{6}x+40=16×18$ .

Simplify this to $\frac{1152}{30+x}+ \frac{5}{2}x=69$

$1152+(30+x)(\frac{5}{2}x-69)=0$

$1152+\frac{150}{2}x+\frac{5}{2}x^2-2070-69x=0$

$\frac{5}{2}x^2+6x-918=0$

The nonnegative solution is $x=\frac{-6 + \sqrt{36+9180}}{5} = \frac{90}{5}=\boxed{18}$

The areas 25 and 40 have same breadth. So the breadth must be their HCF, which is 5. Hence their lengths are 5 & 8 respectively. Now the length of the required area becomes 3 on calculating. The breadth of the area is same as the area of 48, which is 6. Hence the area becomes 18.

The 48 square is the highest. Logically, the area will be the largest.

Let, the segment along the top be x, 16 – x, along the right side be

from bottom to top w, z, y, and 18 – q, where q = y + z + w; then

24 = x(18 – q) = -(16 - x)(18 – q) + 16(18 – q)

24 = 120 + 18x – 16q

8q – 9x= 48

-9(24) + 8q(18 – q) = 48(18 – q)

-27 + q(18 – q) = 108 – 6q

q^2 – 24q + 135 = 0

(q – 15)(q – 9) = 0

Therefore q = 9 0r 15. If q = 15, then 15(16 – x) = 120, 16 – x = 8, x = 8,

(16 – x)y = 32, y = 4, (16 – x)z = 48, z = 6, (16 – x)w = 40, w = 5.

Let the required area be A, and A’ the area of the rectangle on the left

of this rectangle be A’, then

Also, A’/25 = z/w = 6/5, so A’ = 30 = (x – t)z, 6(8 – t) = 30

6t = 18, t = 3.

Then

A = zt = 6(3) = 18.

If q = 9, then 9(16 – x) = 120, 48 – 3x = 40, 3x = 8, x = 8/3.

y(16 – x) = 32, y(40/3) = 32, y = 12/5.

z(16 – x) = 48, z(40/3) = 48, z = 18/5.

w(16 – x) = 40 w(40/3) = 40, w = 3.

As, before, A’ = 30 = (8/3 – t)(18/5) 25/9 = 8/3 – t, t = -1/9 which is

a contradiction.

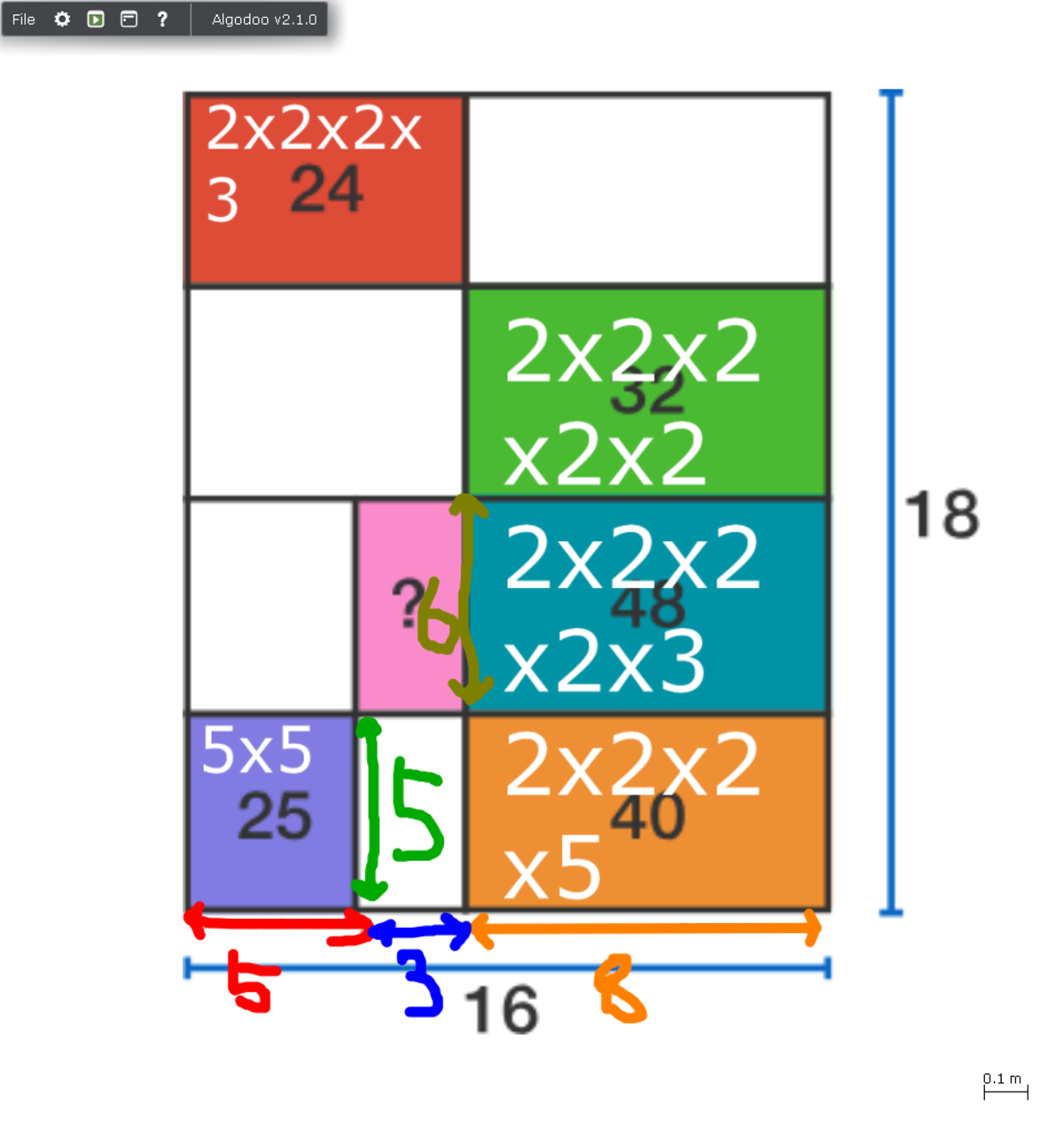
The right hand side rectangles all share the same length $x$ , and the red rectangle has length $16-x$ therefore: $\frac{40}{x}$ + $\frac{48}{x}$ + $\frac{32}{x}$ + $\frac{24}{16-x}$ $= 18$

Multiplying by $x$ gives $40 + 48 + 32 +$ $\frac{24x}{16-x}$ $= 18x$

$120 +$ $\frac{24x}{16-x}$ $= 18x$

Multiplying by $(16-x)$ gives $1920 - 120x + 24x = 288x - 18x^2$

Simplifying gives $1920 = 384x - 18x^2$

Factorising gives $320 = 64x - 3x^2$

Solving the quadratic $-3x^2 + 64x - 320$ gives $x = 8$ or $x =$ $\frac{40}{3}$

Only $x=8$ is a possible solution for this problem therefore the width of the orange rectangle is $40/8=5$ and the purple 'rectangle' is actually a square with sides length 5. The length of the pink rectangle is therefore $16-8-5=3$

The width of the blue or teal coloured rectangle is $48/8=6$ . This equates to the width of the pink rectangle, so the area of the pink rectangle is $6\times3=18$ .

In this problem, it is possible to 'chase' down the lengths of other rectangles to find the side length of the pink rectangle: Notice that the purple rectangle's area is $25$ , which has factors $1, 5, 25$ . If one side were $25$ , this would be bigger than both $16$ or $18$ , so the only option remaining is $5$ and $5$ . Following this, since the heights of the orange and purple rectangles are the same, the orange rectangle has a length of $\frac{40}{5} = 8$ .

Since the largest rectangle has a width of $16$ , the pink rectangle's length is $total - purple \ rectangle - orange \ rectangle$ or $16 - 5 - 8$ , which is $3$ .

We already know that the width of the orange rectangle is $8$ . Because the turquoise and orange rectangles share a side, the turquoise rectangle's height is $\frac{48}{8} = 6$ .

From this information we can deduce the length and width of the pink rectangle. Calculating $(3)(6)$ gives the area of the rectangle, which is $18$ .