57 of 100: Curious Calculator
You have a calculator with 4 buttons as shown; they multiply the current value shown on the calculator by 2, divide the current value by 3, add 5 to the current value, or subtract 7 from the current value.
If the screen starts at 6 , what is the fewest button presses you need to make to get a value of 1 ?
Hint: If working forwards from 6 is daunting, try working backwards from 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
28 solutions
You utterly destroyed this problem!
Log in to reply
I couldn't find a clever way to do this! I'm still waiting for better solutions!
Log in to reply
Any proof that four is the minimum number of steps necessarily involves a proof that it is possible with four steps, and that it is impossible with three or less. A proof that it is impossible in one step involves showing that none of the outcomes of one step result in an answer of 1. This is likewise true of the proofs for two and three steps. There are 64 possible combinations of three keys, since repetition is allowed, and since most of the combinations presents unique cases, there are not a lot of ready shortcuts for eliminating multiple combinations at once. Therefore, any proof would have to have nearly the complexity of the tree diagram, and likely with less clarity!
Nice solution. I used a tree diagram to find the answer as well.
It is interesting to note how the problem could be solved by using a smaller combination of the four keys. The problem can be solved in a minimum of 7 steps by using only the (+5) and (/3) keys. It can be solved in a minimum of 11 steps by using only the (+5) and (-7) keys. It cannot be solved by using any other combination of two keys alone. It can be solved by using any combination of three of the keys. Of course, if the (+5) or (/3) keys are excluded, the minimum is still 4 steps. If either if the (x2) or (-7) keys are excluded, the minimum is 5 steps. If you are not already tired of the problem, you can amuse yourself by verifying this!
If you'd like a smaller diagram, you could do two levels of the trees on either side. 16 numbers on each side instead of a 64-element table.
This is so beautifully laid out - and as @Kazem Sepehrinia has pointed out - it doesn't just show this can be done in 4 steps, but that it can't be done in fewer. I started doing a similar tree, but got in a muddle. I guess asking this shows how old I am - but what software did you use to create your diagram?
Log in to reply
I'm not very good with graphic software! I entered the numbers to a table in word and did the rest with paint, which there is a sad news about it!

Microsoft has said that it won't be updated anymore! I do all my graphic with it.
Log in to reply
I have only just learned how to use paint for a number of printables - and now it's going - I despair!
And if any of you out there are also teachers, can I recommend https://www.mathsisfun.com/games/broken-calculator.html which you can ratch up an intelligence level or 2 by adding 'who can do it in fewest button presses'
Does anyone know of the CS side to this problem? How to find the shortest route across two trees efficiently?
Log in to reply
Using Dynamic Programming you can solve it in O(n) time I believe https://repl.it/Jp9M/3
Note: this method is actually inaccurate because intermediate values can't be negative or over whatever max you set, but that can be fixed by changing the way you set up the array. EDIT: This is that idea implemented. I also included the steps in the printing so you can see how to get to each number as well as the number of steps: https://repl.it/Jp9M/19
All the possible solutions that require only 4 steps are:
- 6 × 2 → 1 2 × 2 → 2 4 ÷ 3 → 8 − 7 → 1
- 6 × 2 → 1 2 ÷ 3 → 4 × 2 → 8 − 7 → 1
- 6 + 5 → 1 1 − 7 → 4 × 2 → 8 − 7 → 1
- 6 ÷ 3 → 2 × 2 → 4 × 2 → 8 − 7 → 1
- 6 − 7 → − 1 × 2 → − 2 × 2 → − 4 + 5 → 1
- 6 − 7 → − 1 × 2 → − 2 + 5 → 3 ÷ 3 → 1
- 6 − 7 → − 1 + 5 → 4 × 2 → 8 − 7 → 1
It is interesting to note the frequencies with which the operations are used in the seven possible 4-step solutions, and how they are distributed by each step. The (-7) key is used 9 times in the seven solutions, and its distribution across the four steps is [3,1,0,5]. In other words, it never occurs as the third step, but occurs in 5 of the seven solutions as the fourth and final step. Likewise, the (x2) key is used 11 times, and its distribution is [2,4,5,0]. The zero is not surprising, since you can't arrive at 1 by multiplying an integer by 2. The (+5) key is used 4 times, and its distribution is [1,1,1,1]. Fascinatingly, the (/3) key is also used 4 times, with the exact same distribution: [1,1,1,1].
A great follow up question would be: how do we know that 4 steps is the minimum? Is there a way we can approach this problem or perhaps even generalize it to see that 4 is, in fact, the minimum number of steps required to reach 1 without having to list out possibilities?
Log in to reply
I don't know, Zach. I certainly listed the possibilities. Take a look at the Collatz conjecture for an example of an even "simpler" problem that no mathematician has been able to reduce to the kind of predictability you are talking about.
Log in to reply
Ah yes, I am familiar with that conjecture. It's amazing how a problem that can be understood by 5 year olds stump even the greatest of mathematicians!
Well there are 4 numbers that are one step from 6 going forward and 4 numbers one step before 1 going backward. To show there is no solution in three steps you need only show there's no one-button step from any of the first four to any of the last four.
Nice work! I think your first sentence should read something like, "Here are all the possible solutions that require only 4 steps." I imagine that there are an infinite number of solutions that use more than 4 steps.
Log in to reply
Oh yes, you are right, thanks.
WOW! I never thought that there are so many ways to do it.
First step 6 x2=12
Second step 12/3 = 4
Third step 4 x2= 8
Fourth step 8 - 7 =1
6-7=-1
-1*2=-2
-2+5=3
3/3=1
The fastest way to get to 1 is done in 4 steps :
1) 6 ÷ 3 = 2
2) 2 × 2 = 4
3) 4 × 2 = 8
4) 8 - 7 = 1
You can use Python to write a program that uses recursion to find out the solution! :)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
All the 7 ways to get 4. There are 256 possible button push combinations (consider each button a digit in base 4, count all 4 digit numerals in base 4, 4 4 = 2 8 = 2 5 6 ). Examine the 16 two button pushes (conveniently arranged in a 4x4 table). Find that 4 occurs 4 tines, 24 once, and -2 once. Find also that these are the only combinations that lead to a solution, and that none are 1 nor yield 1 with one more button therefore no 2 or 3 button solutions, four pushes is the minimum.
These yield at total of 7 solutions. 4 can be finished off one way, x2, -7 yielding 4 independent solutions. 24 can be finished one way ÷3, -7. -2 can be finished two ways, +5, ÷3, and x2, +5.
Two ways to finish off -2 after two pushes.
-1,-2,3,1 (-7,x2,+5,÷3) uses each button once. Arguably prettiest.
-1,-2,-4,1 (-7,x2,x2,+5) no divide.
One way to get 24 and finish it off.
12, 24, 8, 1 ( x2, x2, ÷3, -7) no add.
Four ways to get 4 in two pushes.
12, 4, 8, 1 ( x2, ÷3, x2, -7) no add.
-1,4,8,1 (-7,+5, x2, -7) no divide.
11, 4, 8, 1 (+5, -7, x2, -7) no divide.
2, 4, 8, 1 ( ÷3, x2, x2, -7) no add.
Three ways but all 4 steps.
\[\begin{array} {} 6 & \boxed{\times 2} = 12 & \boxed{\div 3} = 4 & \boxed{\times 2} = 8 & \boxed{-7} = 1 \\ 6 & \boxed{+ 5} = 11 & \boxed{-7} = 4 & \boxed{\times 2} = 8 & \boxed{-7} = 1 \\ 6 & \boxed{-7} = -1 & \boxed{+5} = 4 & \boxed{\times 2} = 8 & \boxed{-7} = 1 \end{array} \]
Big footprint, little content.
1) 6 - 7 = -1 2) -1 * 2 = -2 3) -2 * 2 = -4 4) -4 + 5 = 1
6-7= -1 -1x2=-2 -2x2=-4 -4+5=1
6x2=12 12x2=24 24/3=8 8-7=1
Subtract 7 from 6, leaving you with -1.
Multiply -1 by 2, leaving you with -2.
Add 5 to -2, leaving you with 3.
Divide 3 by 3, leaving you with 1.
6 - 7 = -1; -1 x 2 = -2; -2 + 5 = 3; 3 / 3 = 1 Ans
First step 6 − 7 = − 1
Second step − 1 × 2 = − 2
Third step − 2 + 5 = 3
Fourth step 3 ÷ 3 = 1
6 - 7 = -1 => -1 * 2 = -2 => -2 * 2 = -4 => -4 + 5 = 1
- 6 -7 = -1
-1 x 2 = -2
-2 +5 = 3
3/3 = 1
6 + 5 = 11, 11 - 7 = 4. 4 x 2 = 8, 8 - 7 = 1, therefore there are 4 button presses.
6-7 = -1, -1x2 = -2, -2+5 = 3, 3/3 = 1
One solution : 6 2 2/3 - 7 = 24/3 - 7 = 1 . This requires 4 steps. To prove that we cannot get a value of 1 with less than 4 steps, 1 brute force approach is to calculate all the 16 combinations of 2 calculator operations , check if 1 is amongst any of them. If not, for each of the 16 values above, calculate if any of the calculator buttons yield a value of 1. If not, we are done. The above is not that complex since values would be repeated and many can be discarded at a glance
All solutions for 4 or 5 steps, without permutations of sums/substractions and multiplications/divisions ( +5 –7 × 2 –7 will be shown, but not –7 +5 × 2 –7)
×2 ×2 /3 -7
+5 -7 ×2 -7
-7 ×2 ×2 +5
-7 ×2 +5 /3
×2 +5 -7 -7 /3
×2 /3 +5 /3 /3
×2 -7 ×2 -7 /3
×2 -7 -7 ×2 +5
+5 ×2 -7 -7 -7
+5 +5 -7 /3 /3
/3 -7 -7 /3 +5
-7 ×2 +5 +5 -7
It is simple, very simple. You have to just do the following: 6 + 5 (one) - 7 (two) * 2 (three) - 7 (four). In this way, it could be done by pressing just four buttons.
Here is one solution: 6 ( - 7 ) then ( * 2 ) then ( + 5 ) and finally ( / 3 ) to get 1. This accounts for a total of 4 steps.
6 - 7 = -1 -1 x 2 = -2 -2 x 2 = -4 -4 + 5 = 1
To get to 1 with two operations, you need to get to 2 1 = 0 . 5 , 1 − 5 = − 4 , 1 ∗ 3 = 3 , or 1 + 7 = 8 in a single step from 6 —clearly not possible. To get to 1 in three operations, you need to be able to get to any of those four numbers in two steps, but the only ones that look like they can possibly be reached in two steps are 1 ∗ 3 = 3 and 1 + 7 = 8 . So see if you can get to one step away from either of those two in only one step from 6 —the numbers that are one step away from those are 2 3 , 4 , 3 , − 2 , 2 4 , 9 , 1 0 , 1 5 . You can't get to any of these numbers with only one operation. So sequences involving four button presses are the shortest sequences possible. (Look at other solutions to find those sequences.)
I have found six solutions of length (so far). To find them all I need to develop an algorithm that enumerates all the 256 possible strings of the four characters and tests them all. This should not be too hard.
http://www.codeskulptor.org/#user43 n263Hpy25L 0.py
It takes 4 steps. One possible way is:
6 divided by 3 = 2
multiplied by 2 = 4
multiplied by 2 again = 8
minus 7 = 1




Start from 1 and construct backwards. Going one step forward from 6 shows that we must get one of 12, 11, 2, or -1 in backward construction.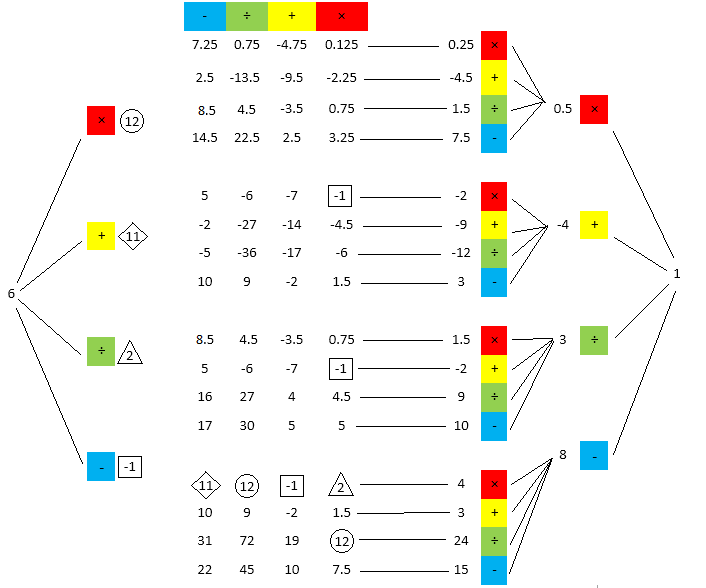 It can't be done with three steps. But with four, 6 appears and there are seven ways to do it. Thus the minimum required button presses is
4
.
It can't be done with three steps. But with four, 6 appears and there are seven ways to do it. Thus the minimum required button presses is
4
.