58 of 100: Squares Within Squares Within Squares...
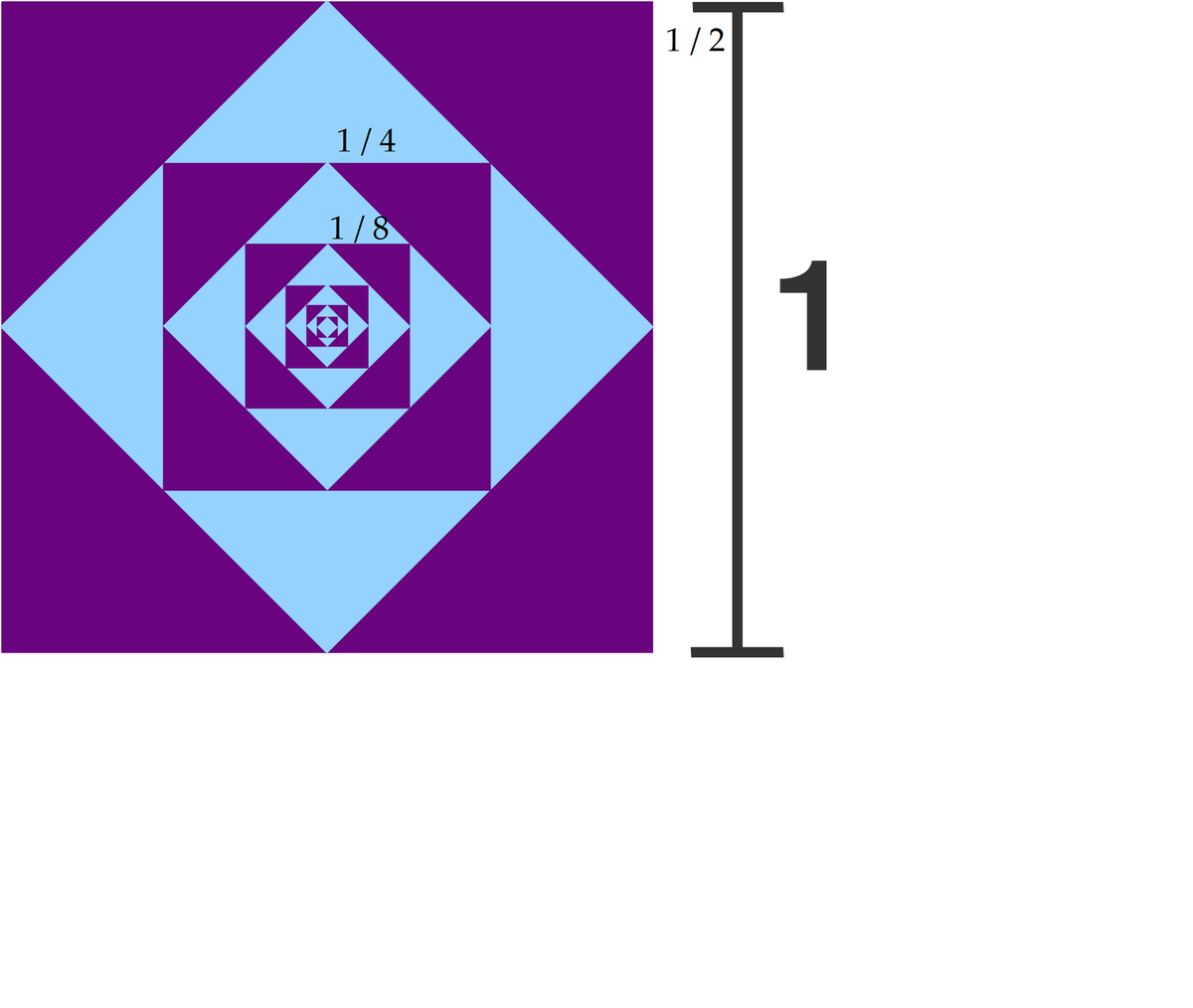
Starting with a unit square, a series of smaller squares is made by repeatedly connecting the midpoints of the sides of each square in turn. Given how the pattern is shaded, approximately what total area is shaded purple?
An approximation is good enough to solve this puzzle; more advanced solvers should do a proof! And you don't need to add up infinitely many fractions to find the answer, there's a faster way!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
27 solutions
 There are infinitely many of the above colored shape in the square and all of them are similar.
There are 12 equal blue and purple triangles in it. Fraction of purple area will be 8/12=2/3. Thus total purple area is 2/3.
There are infinitely many of the above colored shape in the square and all of them are similar.
There are 12 equal blue and purple triangles in it. Fraction of purple area will be 8/12=2/3. Thus total purple area is 2/3.
I did it the exact same way :D So cool ^_^
They are similar rather than being congruent . (Otherwise, this is a neat explanation.)
Great explanetion, clear and simple.
Each successive square is 2 1 the size of the previous square. Thus each colored region is 2 1 of the previous one.
So, the purple regions are of size: 2 1 , 8 1 , 3 2 1 , 1 2 8 1 ...
So we just need the sum of a geometric series:
S = 1 − r a 1 where r = 4 1 and a 1 = 2 1
S = 3 2
For each light blue triangle there is a purple triangle twice as large.
I would quibble with the description "twice as large". Generally, this means that the side lengths are twice as large. You meant that the "area was twice as large", which should be explicitly stated to avoid misunderstanding. My quibble aside, your insight was ... brilliant!
A great first solution :)
Thanks Kazem!
This!!!!!!
Consider the following cutout:
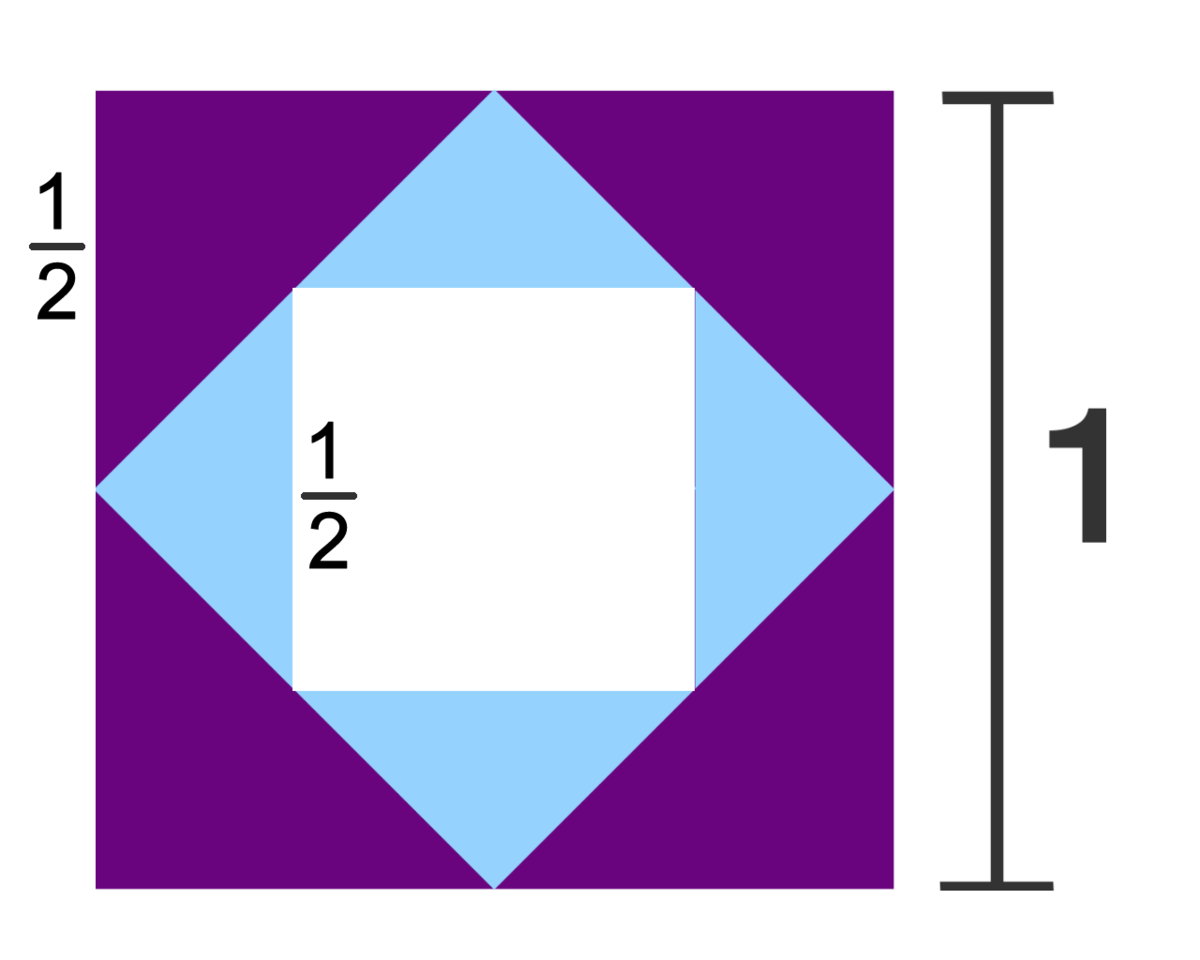
The total coloured area is 1 2 − ( 2 1 ) 2 = 1 − 4 1 = 4 3 , whilst the total purple area consists of four triangles of base and height equal to a half.
Hence the purple area is 4 × 2 1 × 2 1 × 2 1 = 2 1 .
This gives the fraction of the purple area in this cutout being equal to 2 1 ÷ 4 3 = 3 2 .
The ratio remains the same if we were to continue adding these cutouts within each other, so the total purple area is equal to 3 2 .
Let A be the area of the whole figure we are looking for.
Look at the first level inner square. It is a copy of the whole figure but 2 1 length on the side, this can be seen from symmetry. So it is 4 A the area.
The whole figure consists of four purple triangles, each of area 8 1 , plus the area of the inner square. This gives:
A = 4 8 1 + 4 A
Rearrange and solve for A :
A = 4 2 + 4 A
A = 4 2 + A
4 A = 2 + A
3 A = 2
And finally:
A = 3 2
I solved is as an infinite series, by defining the area as
A = 1 - 2 1 + 4 1 - 8 1 + 1 6 1 ...
which means that
- 2 A = - 2 1 + 4 1 - 8 1 + 1 6 1 ...
and if we subtract the the two equations from each other we get
A + 2 A = 1
or written another way
A = 3 2
 As shown above the sum of purple area in first square is (
2
1
*
2
1
) / 2 * 4 =
2
1
As shown above the sum of purple area in first square is (
2
1
*
2
1
) / 2 * 4 =
2
1
in third square it is (
4
1
*
4
1
) / 2 * 4 =
8
1
in every step it is divided by 4 therefore the sum of areas would be : (
2
1
+
\frac{1}{8} + ... = \(\frac{1}{2}
/ ( 1 -
4
1
)=
2
1
/
4
3
=
3
2
This is not right. the first, largest square's purple shade covers 2/3 of the shape. Therefore the purple shading is the same throughout the squares. Therefore the purple shading ( all of the shading ) is 2/3 shaded by purple, because all the squares are in the same ratio, purple to blue equals 2/3.
This square is illustrating the geometric series with a_1=1 and r=-0.5. Essentially, we start with 1 unit purple, then "lose" half the area as it turns blue, then gain back half of what was lost, then lose half of what we gained back, etc.
So, we simply have S = 1/(1 - (-0.5)) = 1/1.5 = 2/3
The purple regions form an infinite geometric series with first term equal to 1/2 and common ratio equal to 1/4 (or 1/2 + 1/8 + 1/32 + ...) The formula for infinite geometric series is 1 − c o m m o n r a t i o f i r s t t e r m . Thus, the sum of the purple regions = 1 − 1 / 4 1 / 2 = 3 / 4 1 / 2 = 3 2
The biggest people square is area 1. Subtract the biggest blue square of area 1/2. Add the second purple of area 1/4, subtract blue 1/8 etc. The common ratio is -1/2 which you plug into the infinite geometric series sum to get 2/3
After the first interaction the problem is the same, but rescaled with a factor 4. Thus:
S = 2 1 + 4 S ,
and then:
S = 3 2
For each step, you remove half of what you just added, or you add half of what you just removed. If you write the area as a binary number, it would be 0.101010101..., which can be divided by 2 to get 0.0101010101..., then multiplied by 3 to get 0.11111111..., which is 1. Since we multiplied the area by 3/2 to get one, the area must be 2/3.
It is a problem of G.P.
Area of Purple Region = Sum of Area of Purple Squares - Sum of Area of Blue Squares
On calculating sides of squares:
-
Purple Squares, its sides will form a series like this : 1, 2 1 , 4 1 , …
-
Blue Squares, it will form a series like this : 2 1 , 2 × ( 2 ) 1 , 4 × ( 2 ) 1 , …
Area of Purple Region = Area of Purple Squares - Area of Blue Squares
= 1 − ( 4 1 ) 1 - 1 − ( 4 1 ) ( 2 1 )
= 3 4 - 3 2
= 3 2
It is a geometric series of r = -1/2 and the first term is 1. Summing the series gives 1/(1-(-1/2)), which equals to 2/3
A solution based on the approximation hint. It has the virtue that the ultimate result of 2/3 becomes apparent early on.
 Compare this problem to an earlier Problem of the Week
Compare this problem to an earlier Problem of the Week
The sum of the purple areas can be expressed by the sum ∑ x = 0 ∞ 2 2 ( x + 1 ) 2 , which gives the solution of 3 2 .
I approached it by subtracting the blue from the total to get purple. - We observe that each side is 2 2 of the previous side. For the first side, we go by subtracting the smaller purple from the first blue one and then doing the same to the even smaller ones. 1-[ 2 1 - 4 1 + 8 1 - 1 6 1 ......] This gives us 3 2
You can fill half of the square with three of each size of purple triangles
So all purple triangles will be 3 2 of the square.
This is the way, I visualized it. The first sum -1 is the half of the second sum. It is known that 1 + 2 1 + 4 1 + 8 1 + ... converges against 1, and the solution is a fraction with the numerator 2n and the property: 1 = 3 n n + 3 n 2 n or shortened 1 = 3 1 + 3 2
Pink Area = 4(1/2)(1/2)(1/2) + 4(1/2)(1/4)(1/4) + 4(1/2)(1/8)(1/8) + ……..= 1/2{1 + 1/4 + 1/16 + ……..) = 1/2[1/(1 – 1/4)] = 1/2(4/3) = 2/3.
The area is represented by the serie 1 + (-1/2 + 1/4 - 1/8 + ...) where a1 = -1/2 and r = -1/2. So,
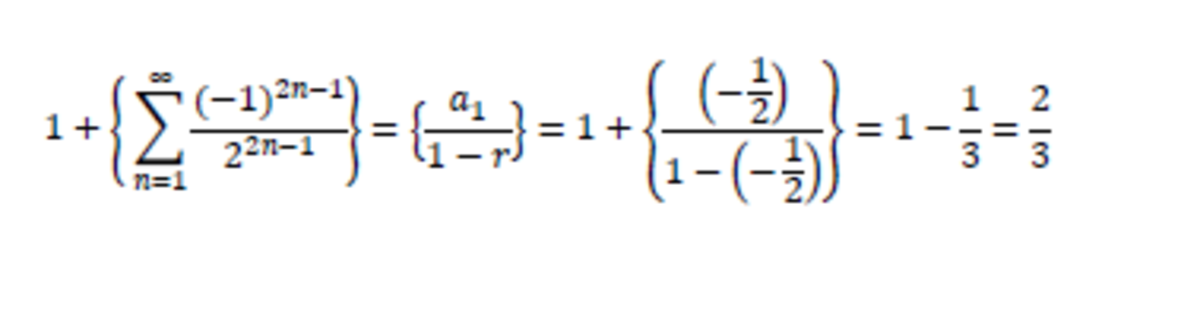
The 4 largest triangle have an area of 2 1 , the next 8 1 , ...
Let x = 2 1 + 8 1 + 3 2 1 . . . . We notice that 4 x = 2 + 2 1 + 8 1 + . . . = 2 + x . Thus, x = 3 2 .
Since all the squares are the same, only take the first square. This means that the purple area will cover 2/3 of the entire square, therefore the whole shape is 2/3 shaded purple.
Let a 1 2 be the area of the first, greatest square. Then, the area of a second square is a 2 2 = 4 a 1 2 + 4 a 1 2 = 2 a 1 2 .
More generally, a n 2 = 2 n − 1 1 × a 1 2 .
Purple area can be expressed as:
A p u r p l e = a 1 2 − a 2 2 + a 3 2 − a 4 2 + . . . = a 1 2 − 2 a 1 2 + 4 a 1 2 − 8 a 1 2 + . . .
That's an infinite geomtric series with common ratio − 2 1 that sums to:
A p u r p l e = 1 − ( − 2 1 ) a 1 2 = 2 3 a 1 2 = 3 2 × a 1 2 = 3 2
By the midpoint formula, Purple Area of the 1st square = (1-(1/2)*1) = 1/2
Every unrotated square has 1/4 the area of the previous unrotated square,of which 1/2 is shaded purple . The sum of all these areas forms an infinite geometric progression with starting term a = 1/2 and common ratio r = 1/4
The total purple area = [(1/2)]/[(1-(1/4))] = [1/2] / [3/4] = 2/3
The total area of the square is 1, so the total area shaded purple is equal to the proportion of purple area to the overall area. Since the pattern repeats, we can disregard the repetitions and consider only the proportion of the first iteration.
The purple area is composed of 4 triangles of area 1/8th each for a total area of 1/2. The cyan area is similar, occupying half of the remaining half of the square, or 1/4. The total area of the first iteration is therefore 3/4, and the proportion shaded purple is 2 1 / 4 3 = 3 2
Purple are of a square of side of length A is equal to 0.5A*A.
Using elementary geometry, it can be shown, that next purple area is equal to 0.25 of the previous.
That is purple ar[i] =0.25*purple ar[i-1]
And we know that the first square's side is 1 unit.
So purple_ar[0]=0.5
We are finding the infinite sum:
S=purple ar[0] + purple ar[1] + purple_ar[2]...
It can be rewritten as :
purple ar[0] + purple ar[0] k + purple_ar[1] k*k...
Where k=0.25
If we subtract S*k from S we would get:
S*(1-k)=puple_ar[0]
Since the last member contains k of power infinity it is almost equal to zero and can be not count since we are finding approximately area
Finally:
S=0.5/(1-0.25)=2/3