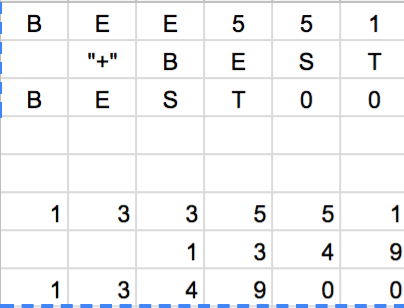
61 of 100: BEST BEE
× B E B E E 5 S 9 5 T 9 1
If each letter represents a different nonzero digit, what must B be?
Our cryptogram puzzles are getting tougher, and they will get tougher yet before the summer is over!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Nice! This was my first instinct as well. Times 99 made me think immediately of divisibility rules for 9 and 11.
Thanks! I had never seen your "divisibility-by-11" rule before. If there is anyone out that also has not seen your rule before then this little tidbit might help: BEE551 is a 6-digit number. If BEE551 is a multiple of 11 then it must be the product of 11•(5-digit number). The (5-digit number) may be represented as JKLMN or [J][K][L][M][N] where [J]{K][L][M][N] means N•1 + M•10 + L•100 + K•1000 + J•10000 and J, K, L, M and N are each single digits. 11•JKLMN is equal to JKLMN + JKLMN0.
11•JKLMN = [J][J+K][K+L][L+M][M+N][N} which is an "equivalent" 6-digit number that is a multiple of 11.
The rule can be generalized to any N-digit number. Specifically , for our 6-digit number if you sequentially and alternately add and subtract the digits you get 0: –J + (J+K) – (K+L) + (L+M) – (M+N) + N = 0.
So that's how I understand your "divisibility by 11" rule.
Your rule is a much more generalized version of the "divisibility-by-11" recursively reductive rule that I was familiar with: if Pq represents a number K where it is understood that K = q + P•10 and that q is a single digit whereas P may be any number of digits then Pq is a multiple of 11 if and only if P-q is a multiple of 11.
Here's an example of the recursive reductive "divisibility-by-11" rule:
Is 133551 a multiple of 11? Yes, IFF 13355 – 1 = 13354 is a multiple of 11.
Is 13354 a multiple of 11? Yes, IFF 1335 – 4 = 1331 is a multiple of 11.
Is 1331 a multiple of 11? Yes, IFF 133 – 1 = 132 is a multiple of 11.
Is 132 a multiple of 11? Yes, IFF 13 – 2 = 11 is a multiple of 11.
11 is obviously a multiple of 11 with the result that 133551 is also a multiple of 11.
Another example:
Is 678 a multiple of 11? Yes, IFF 67 – 8 = 59 is a multiple of 11.
Is 59 a multiple of 11? Yes, IFF 5 – 9 = -4 is a multiple of 11.
–4 is obviously not a multiple of 11 with the result that 678 also is not a multiple of 11.
Finally, –6 + 7 –8 = –7 ≠ 0 so 678 is confirmed to not be a multiple of 11.
Again, THANKS!
Your solution is nice! It's a fast way to solve this problem!
Great solution, assuming the problem is solvable, which I guess is okay. If the 99 had been, say 77; then, you would reach the same conclusion; but, there would be no values for E, S, and T that would make it work.
Log in to reply
Thanks for bringing up this point :) I solved it like a test! There is only one correct choice.
Phenomenal and deceptively simple insight, Kazem :)
Nice one! One criticism: you have not proven that the problem actually has a solution. You only have shown that, if there is a solution, then B = 1 .
Log in to reply
Thanks :) Actually, I looked at choices. If there was another choice, I would continue my reasoning to show that indeed there is a solution.
It goes like this: B E E 5 5 1 is divisible by 9 . Then 2 E + 3 is divisible by 9 . Thus E = 3 . Divide 1 3 3 5 5 1 by 9 9 to get other digits.
Holy Nellie... What a great approach! (+1)
@Kazem Sepehrinia , do u mind if i make a problem named "in memory of maryam mirzakhani"?
Since 9 9 ⋅ B E S T = 1 0 0 ⋅ B E S T − B E S T , we rewrite the problem as B B E E B E S E 5 T S 5 0 T 1 0 + This can easily be solved working from right to left. We find 1 3 4 9 + 1 3 3 5 5 1 = 1 3 4 9 0 0
Nice insight, Arjen!
Ah, great approach!
Great! I used the same method! Is easier to solve a sum than a multiplication!
Good solution. I did this a long way around figuring out first T then S then trying to find E
which I only did by trial and error, which I know is a totally unsatisfactory way of doing the problem. Good thinking by you! Regards, David
B E S T * 99 can be written as : BEST*(100-1) = BEST00-BEST as shown in the following :
B E S T 0 0
_ B E S T
B E E 5 5 1
T = 9
S = 4
E = 3
It is obvious that there is no carry involved in the subtraction involving B ( since the leftmost digits BE are brought into the final total as they are)
Hence, S-B = E
B = S - E
= 4 - 3
= 1
Same method:)
I mixed the methods, I guess - you can see T = 9 from the original sum, and put that into BEEST00 - BEST
I did that too
Take your pick.

Thank you for restoring the upload dialog. I was unable to drop or paste into the "drop pictures here" form.
9T = 81, T = 9 9S + 8 + 1 = 45, 9S = 36, S = 4 9E + 4 + 4 = 35 E = 3
9B + 3 + 1 = 13, B = 1
One can actually check that is the solution.
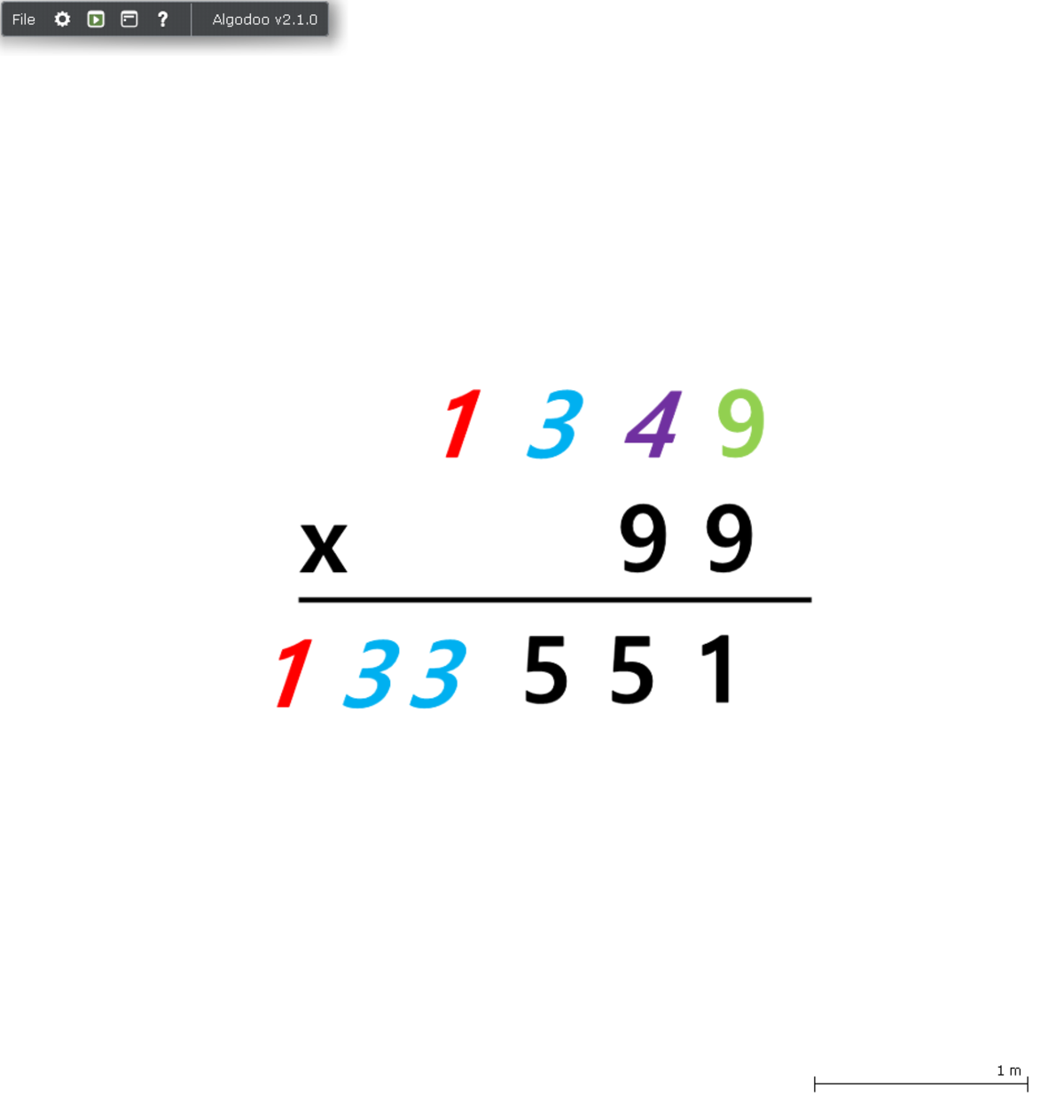
Easiest to convert this to another addition problem by using
then working from right to left easy to get:
1 3 3 5 5 1 1 3 4 9 1 3 4 9 0 0
B E S T × 9 9 = B E E 5 5 1
so, the answer is divisible by 99 or 33 or 11......................[it works everywhere]
so, it could be, .....(1)...... 9 − 4 5 + 4 5 − 9 E + 9 E − 9 B or, 9 B = 9 or, B = 1 ........................[for 99]
secondly, 3 − 1 5 + 1 5 − 3 E + 3 E − 3 B or, 3 B = 3 0r, B = 1 ....................................[for 33]
same for, 11
The problem can be cast as : BEST*(100-1) = BEST00 - BEST which is a much easier subtraction problem since 3 digits are already known
As there are two carry digits and you are only adding two numbers , therefore the maximum number B can be is 1
If you would like to use a bit of brute force...
It's clear that s=4 and t=9 if we consider that BEST x 100 must end in 00. Since BEE551 must be divisible by 9 and 5+5+1=11, we know that B+E+E equals either 7 or 16. Given that each letter represents a different non-zero digit, most possible cases are eliminated.
If B+E+E=7, we could have either B=7 with E=1 or B=5 with E=2. If B+E+E=16, we could have B=6 with E=5 or B=2 with E=7.
Plugging in these values makes the answer easy to verify.
B=1. Here is a program in JustBASIC:
for b=1 to 5
for e=1 to 9:if e=b then [ne]
for s=1 to 9:if s=b or s=e then [ns]
for t=1 to 9:if t=b or t=e or t=s then [nt]
best=1000*b+100*e+10*s+t
bee551=100000*b+10000*e+1000*e+551
if best*99=bee551 then print best;" x 99 = ";bee551
[nt]next t
[ns]next s
[ne]next e
next b
1349 x 99 = 133551.
WOW HOW DID HE/YOU DO IT!
The solution is 133551, so the answer is 1
I found this by using every combination of (B, E, S, T), then minimizing the squared error of BEST * 99 and BEE551. Per the below R code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
|
BEST x 99 = BEST x (100 - 1) = BEST00 - BEST = BEE551
That mean's 10 - T = 1. Thus, T = 9. 9 - S = 5. Thus. S = 4. 8 - E = 5. Thus E = 3. S - B = E or 4 - B = 3. Thus, B = 1 .
As we multiply by 99 by x, the last two digits are 100-x.
100-x= 51 . so, x= 49. S=4, T=9.
Since, green star is 7(+4 in hand), so we must multiply 99 by 3 . So, E=3. So, our product is 33551. To get this 3 in second digit form left, we need a 2 similarly. But this 2 should come with a 3 in hand. So B= ( 2-3)/9= *9/9 = *1. Since, the number is one digit only, so *=0. SO, B MUST be 1.
You can solve it absolutely straightforward
Here is a Python script:
http://ideone.com/3owbYW
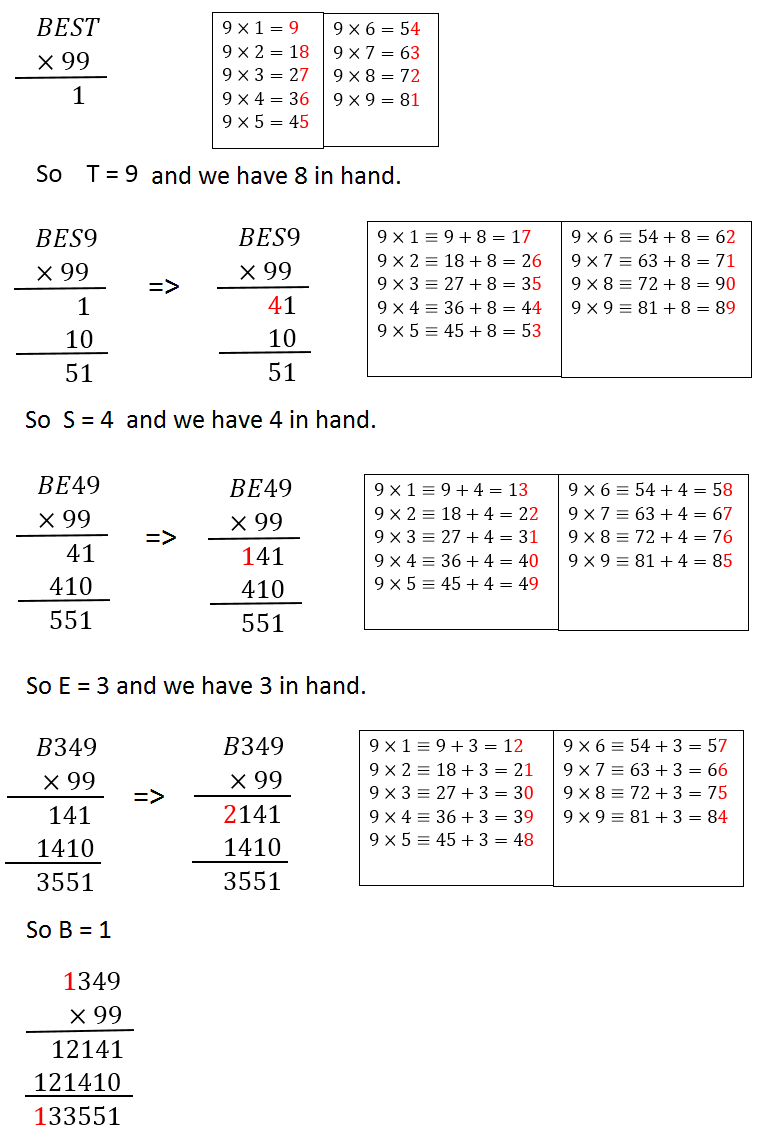
B E E 5 5 1 is divisible by 1 1 . It follows that − B + E − E + 5 − 5 + 1 = − B + 1 is divisible by 1 1 . Thus B = 1 .