65 of 100: It's Also Called A Heptaparallelohedron

Assume there are $n$ vertices. There are two triangles corresponding to every vertex. If you add up all of these (allowing duplicates), there are $2n$ triangles in total. In this sum, each triangle gets counted three times (once for each vertex). So $2n = 3A$ , and $A = 2n/3$ .

Applying the same logic to the squares, $B = n/2$ , and $A > B$ .

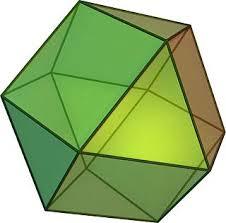Cubeoctahedron can be made from a cube by slicing off vertices to make the triangular faces. 8 vertices result in 8 triangles.

The faces of the original cube, and there are 6 of them, form the square faces of cubeoctahedron. There are therefore more triangles.

Image: Wikipedia

Let $V$ be the number of vertices.

Let $T$ be the number of triangles and $S$ be the number of squares. There are $3T$ vertices, 3 for each triangle, but each vertex is counted twice, thus $V=\frac{3T}{2}$ . There are $4S$ vertices, 4 for each square, but each vertex is counted twice this way, thus $V=2S$ . Thus $\frac{3T}{2}=2S$ and $T=\frac43 S>S$ .

Let $E$ be the number of edges and $F$ be the number of faces.

According to Euler characteristic $V-E+F=2$ . Thus $2S-(3T+4S)/2+(S+T)=2$ or $T-S=2$ . Combine this with $\frac{3T}{2}=2S$ . It gives $T=8$ and $S=6$ .

There are four triangles around one square and only three squares around one triangle

So I have guessed intuitively

Note that every edge has a triangle on one side and a square on the other. No edge has only triangles on either side or only squares on either side. Counting the edges will determine which shape has more, as follows: If we erase the triangle faces, all of the edges may be attributed to squares. Let the number of squares be S and the number of edges be 4S. Similarly, if we erase the square faces, all of the edges may be attributed to triangles. Let the number of triangles be T and the number of edges be 3T. Since the number of edges must be same, 3T = 4S, which leads immediately to the result T = (4/3)•S. Therefore, the number of triangles is greater than the number of squares .

Draw red dots in the corners of each square and blue dots in the corners of each triangle.

Around each vertex there are $2$ blue dots and $2$ red dots: $D_3 = D_4 = 2V$ ;

In each triangle there are $3$ blue dots, and in each square $4$ red dots: $D_3 = 3F_3$ and $D_4 = 4F_4$ .

It follows that $3F_3 = 4F_4$ so that

$\boxed{\text{triangles}\ :\ \text{squares} = 4:3.}$

We can say even more after introducing Euler's equation, $V + F = E + 2$ . For each edge there are two dots, so $2E = D_3 + D_4$ . Thus $V + F_3 + F_4 = E + 2;$ multiply by 6, and write $3F_3 = 2V$ , $4F_4 = 2V$ , $2E = D_3 + D_4 = 4V$ : $6V + 4V + 3V = 12V + 12;$ $V = 12.$ It follows that $D_3 = D_4 = 24$ , $F_3 = 8$ , $F_4 = 6$ , $E = 24$ .

More generally, if at each vertex there are $m_1$ $n_1$ -gons and $m_2$ $n_2$ -gons, etc. then $F_i = \frac{m_i}{n_i}V,$ $V = \frac{2}{1-\sum_i \left(\dfrac 12 - \dfrac 1{n_i}\right)m_i}.$

Each vertex uses two triangle corners and two square corners, using up 2/3 of a triangle's corners but only 1/2 of a square's corners. Thus, more triangles than squares are needed to account for all vertices.

The ratio for triangles to squares is 4:3

Therefore the number of triangles (A) is greater

Why is this called a Heptaparallelohedron? The only hepta (7) in this solid is the total number of faces which is twice seven. as a truncated cube, there are 8 triangular faces, thus calling it an octahedron makes sense, maybe more so, since each of the square faces with a lesser truncation would be octagons. But I'm puzzled as to why 7.

Next to every triangle face there are 3 squares, one on each side. But around every square there is 4 triangles (one for each of its sides). Therefore, there are more triangles.

Each square has four neighbors, while each triangle has three, so the squares’ neighbours (i.e. the triangles) will be greatest in number.

Rotate the front view of the figure by 120* and then reflect it with respect to the the plane, which is separating the front and back view. Now, we can easily find that there are 6 squares and 8 triangles. I think that this can be generalised for example take the case when we have regular tetrahedrons and prisms forming a 4-D hyperheptaparallelohedron.

Let's count the edges. It's 3x or 4y. Those numbers are equal (x - number of triangles, y - number of squares). If y > x then 4y > 3x if x = y then x = y = 0, so, the last option is there are more triangles than squares

S: number of squares

T: number of triangles

There are 4 triangles around each square, so counting 4 triangles per square and summing up gives 4S. Since there are 3 squares around each triangle, we have here counted each triangle 3 times. Thus, 4S=3T.

Euler's formua says that $V-E+F=2$ for any solid polyhedron. For argument's sake, let's say that the polyhedron contains $t$ triangles and $s$ squares. So $F=t+s$ .

Now to the edges. Triangles have 3 edges and squares have 4 edges, but every edge is counted twice this way. So $E=\frac{3t+4s}{2}=\frac{3}{2}t+2s$ .

Finally, vertices. Triangles have 3 vertices and squares have 4 vertices, and the problem says four shapes meet at each vertex. So $V=\frac{3t+4s}{4}=\frac{3}{4}t+s$ .

Plugging these into Euler, we get:

$(\frac{3}{4}t+s)-(\frac{3}{2}t+2s)+(t+s)=2$

$(\frac{3}{4}t-\frac{3}{2}t+t)+(s-2s+s)=2$

$\frac{1}{4}t=2$

$t=8$

So 8 triangles, which means 24 edges; 24 edges makes 6 squares. There's more triangles than squares.

Every edge is shared by exactly one square and one triangle. So if there are a total of T edges, then there are T/4 squares and T/3 triangles.

T/3 > T/4, thus there are more triangular faces than square ones.

The shape is 3D

Each square will have 4 triangles next to it but each triangle will only have 3 squares next to it.

The solid has 14 faces. If you pass a plane through the middle of the solid, you will see that there are 7 on top and 7 on bottom. It is easy with the use of a transparent picture of the solid to see that there are only 3 squares and 4 triangles on top. This makes the number of triangular faces 8 and squares 6.

Suppose we take every vertex and highlight all four shapes around it. After we do this, there will be overlapping highlights. Since a triangle has three vertices and a square has four, they would be each highlighted three and four times respectively. However, remember that each vertex distributes highlights equally to two squares and two triangles. Therefore, the total number of highlights on squares and triangles must be the same! If a triangle has three highlights each, then there must be more triangles needed to get to exactly half of the total highlights than a square that has four highlights each, since a triangle has less highlights per shape. Therefore, there must be more triangles.

Each square is limited by 4 triangles, but each triangle is shared by 3 squares. So if there are n squares, there will be 4n/3 triangles, which is a number greater than n.

Each triangle connects to three vertices, and each square connects to four vertices. Given that the total number of vertices is constant, and each vertex is connected to the same number of squares as triangles, it takes fewer squares to meet the number of vertices than triangles.

Alternately, each square shares edges with four triangles, and each triangle shares edges with three squares. The total number of edges is constant, so the number of squares required is fewer than the number of triangles.

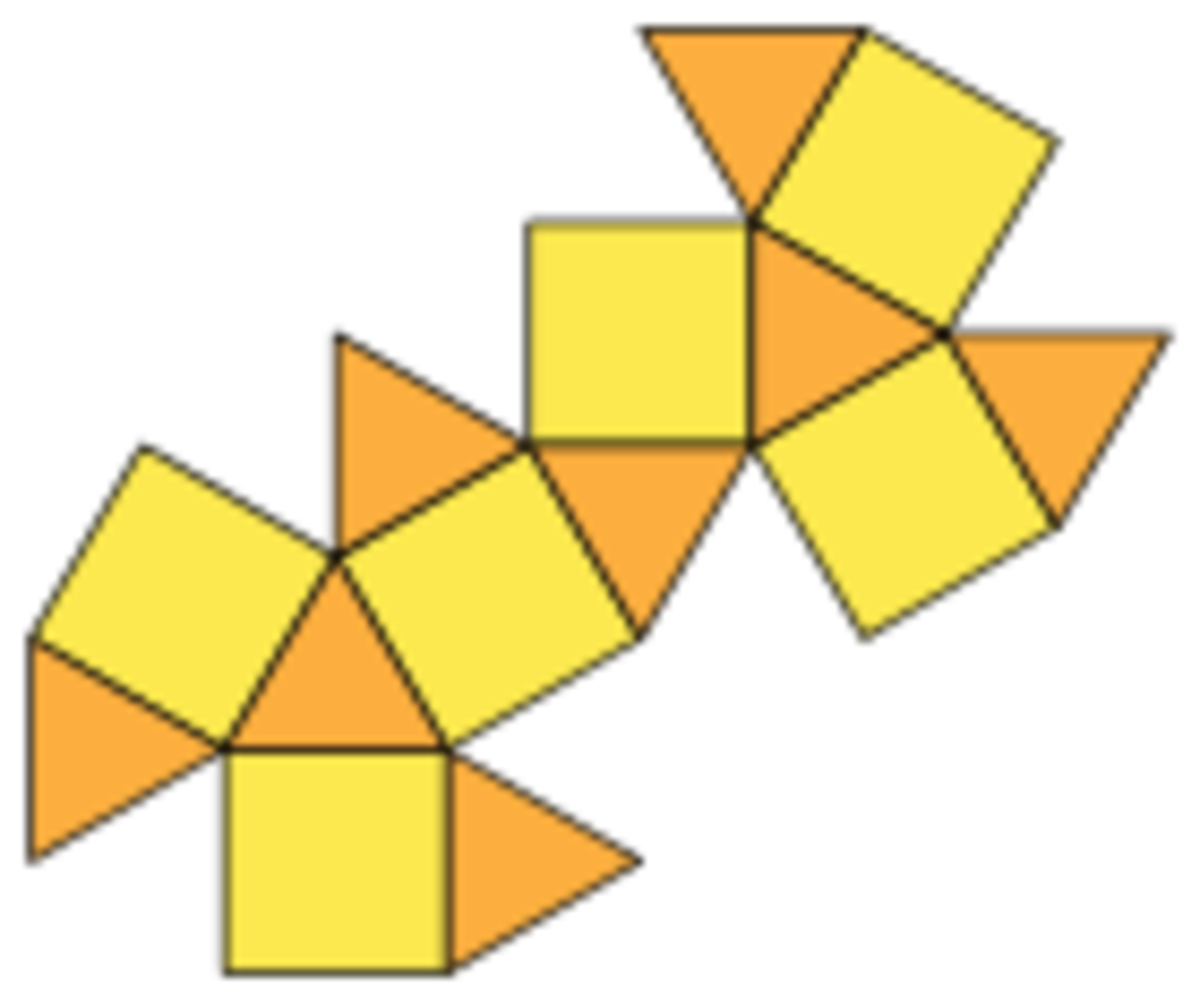
The best way to find out is to visualize a planar net of this solid.

Same number of squares and triangle at all of the vertices therefore

Number of square corners=Number of triangle corners

However, the squares contain 4 corners while the triangles only three

To contain as many triangle corners as square corners, there must be 4/3 of a triangle to every square

The figure is obtained by truncating the vertexes of a cube, so we have 6 squares and 8 traingles from the 8 truncated vertexes.

$\boxed{Solution = A}$

For each triangle, there are 3 squares. For each square there are 4 triangles. Thus the number of triangles have to be greater than the number of squares.

Each triangle shares an edge with three squares. Each square shares an edge with four triangles. Thus E = 3 T = 4 S, which is only possible if T > S.

Above is the net of a Cuboctahedron.

In geometry, a cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive.

A square has 4 vertices and an equilateral triangle 3 vertices. At each vertex, there are 2 squares and equilateral triangles. Greater the number of vertices, lesser the number of faces it takes and vice-versa. So triangle has a greater number of faces.