7 of 100: XX YY ZZ
+ X X Y Z Y X Y Z Z
If each letter represents a different nonzero digit, what must Z be?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
31 solutions
Moderator note:
Nice job! Thinking in terms of place value (for instance, writing the X in the hundreds place as 100X) is a powerful technique that can be easily overlooked with this kind of problem.
This is really nice!
If you rearrange to 10Z + Y = 89, then using place value to interpret, the rest of the answer is clear: Z=8 9=Y
I have no idea what is going on in these things
Nice!! I did the same way :)
Why do XX, YY, and ZZ have to be multiples of 11?
Log in to reply
For any number NN in base 10, NN = 10n + n = 11n. Therefore, NN is a multiple of 11.
why does 11x +11y +11z = 100x + 10y +z?
Great Idea! Super..
Fabulous solution!
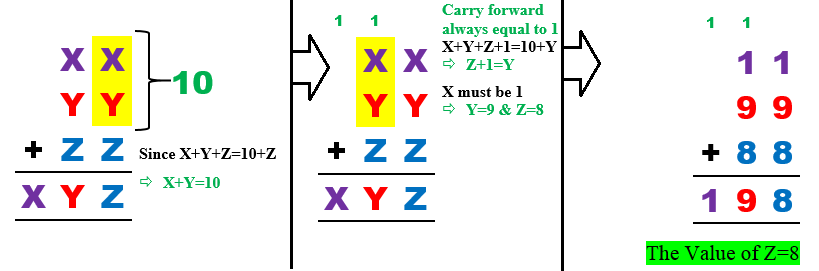
Adding columnwise: 1 st column: X + Y + Z = Z + 1 0 ( ∗ ∗ ) 2 nd column: X + Y + Z + carry 1 = 1 0 X + Y ⟹ Z = 9 X − 1 Since Z is a digit implies X = 1 and Z = 8 ( ∵ for X ≥ 2 ⟹ Z > 1 0 )and for these values Y = 9 . Hence Z = 8 .
∗ ∗ NOTE:- Here carry could be 0 , 1 , 2 accordingly X + Y = 0 , 1 0 , 2 0 respectively but since 1 ≤ X , Y ≤ 9 we are only left to take X + Y = 1 0 .
Nice approach, but you got lucky here. If you're adding three numbers, why would you assume the carryover is 1?
Log in to reply
Assume X+Y+Z=20+Z
Subtracting Z from both sides...
X+Y=20, which is not possible because X and Y are both single digit numbers.
@Rishabh Cool Mentioning this would have been nice in your solution. :-)
Log in to reply
Yep, to be complete the "carry might be 2" case needs to be considered in the answer. This seems to be the missing element in a lot of the answers.
Cool... I've added a note though :-)
No... Carry would be 1 only since X + Y is constrained to take values less than 1 8 only.
Nicest approach here :)
@Samuel Qin . Good point. Thanks.
Even with X + Y = 1 0 it is possible for the carry from the tens to the hundreds to be 2. After all, if Z = 9 then X + Y + Z = 1 9 , which would lead to 1 + X + Y + Z = 2 0 in the tens column... In a complete solution this should be accounted for!
First column says that X+Y=10. This tells us that the second says Y=Z+1. And as X+Z=9, the X in the third column must be 1. Hence, X=1, Y=9, Z=8.
How can you say that X in the third column will be 1 ?
Terry, the 'X' in the third column has to be 1 because it is carried over from 'X+Y' from the second column; since Z+1=Y is a single digit. X+Y also has to be a multiple of 10, and it can only be 10 because they are both single digits. Which means that only '1' can be carried over to the third column which must be 'X'.
Accidentally clicked on the wrong answer, oh well..
This is exactly how I did it, too
I love this solution
Pretty much how I did it! I saw that y must equal z+1, that x+y must be equal to 10, and that x must equal 1. The problem solves itself from there.
i play tennis innit
We know that X+Y=10(X&Y are single digit number and X+Y+Z=10+Z), at max if we put Z=9 also we will get X+Y+Z=19 & X+Y+Z+1=20 which is not allowed as in the problem statement. (X,Y,Z all are different nonzero digit)
While the carry does indeed have to be 1 in this case, I'm not sure if you fully explained why the carry can't be 2.
Log in to reply
We know that X+Y=10(X&Y are single digit number), at max if we put Z=9 also we will get X+Y+Z=19 & X+Y+Z+1=20 which is not allowed as in the problem statement X,Y,Z all are different nonzero digit. Hope now it will be clear.
So looking at the units column:
X + Y + Z = Z m o d 1 0
So it follows, given the single digit nature of X, Y and Z that:
X + Y = 1 0
now looking at the tens column only we have
X + Y + Z + 1 = Y
The 1 appeared due to the carry over from the units column:
as we know X+Y=10 and therefore will give a zero (in this column) we have:
Z + 1 = Y
now looking at the hundreds column we have only the 1 carry over, so:
1 = X
therefore given we know:
X + Y = 1 0
we can deduce:
Y = 9
and from:
Z + 1 = Y
we know now know:
Z = 8
lets test out answer:
1 1 + 9 9 + 8 8 = 1 9 8
CORRECT!
so we can confidently say
Z = 8
We'll consider each numbers separately.
X X = 1 0 X + X
Y Y = 1 0 Y + Y
Z Z = 1 0 Z + Z
X Y Z = 1 0 0 X + 1 0 Y + Z
1 0 X + X + 1 0 Y + Y + 1 0 Z + Z = 1 0 0 X + 1 0 Y + Z
Simplifying this we get,
1 1 X + Y + 1 0 Z = 1 0 0 X
∴ Y + 1 0 Z = 8 9 X
Clearly, X can only take the value of 1 which implies that Y = 9 and Z = 8 .
if my girl and papa john both drowning and i can only save 1.... catch me at my girls funeral with betr ingridates and bter pezza, prapy jhon
Cheers pallerino this worked very well my man
i play tennis innit
kachigga x5 xD
fidgdet spinner is lyf
Method 1 : Brute force algebra! 1 1 X + 1 1 Y + 1 1 Z = 1 0 0 X + 1 0 Y + Z 8 9 X = Y + 1 0 Z . Since Y , Z ≤ 9 , 8 9 X ≤ 9 9 which implies X = 1 .
8 9 = Y + 1 0 Z has the obvious solution Y = 9 , Z = 8 .
Method 2 : Reasoning through the process. Since X + Y + Z = Z , X + Y must end in a zero, therefore X + Y = 1 0 .
The carry from the units to the tens is at most one, therefore the sum of the tens is at most X + Y + Z + c ≤ 1 0 + 9 + 1 = 2 0 . But Y = 0 , which means that the sum of the tens is no more than 19, and X = 1 . It follows that Y = 1 0 − 1 = 9 .
Finally, comparing the units and tens columns we have Y = Z + 1 because of carry. Therefore Z = 9 − 1 = 8 .
Method 3 : Just because nobody posted anything along these lines yet...
Since the three summands are multiples of 11, X Y Z is a multiple of eleven. This means that X − Y + Z is a multiple of eleven. Also, X ≤ 2 , Z ≤ 9 , and Y ≥ 1 implies that X − Y + Z < 1 1 , and obviously X − Y + Z > − 1 1 . Thus X − Y + Z = 0 .
We rewrite this as Y = X + Z , and the sum becomes 2 Y Y = X Y Z . The presence of a hundreds place implies X = 1 , Y ≥ 5 ;
moreover, Z = even, so Y = X + Z odd. Y = 5 is ruled out because Z = 0 .
We are left trying Y = 7 : 2 ⋅ 7 7 = 1 5 4 ; but 7 = 5 ; and X = 9 : 2 ⋅ 9 9 = 1 9 8 ; which works .
X+Y =10 , for Z at the one's place and also, X+Z=9 FOR Y in tens place , here we get that ,Y=1+Z, and possibilities of X are now only 1&2.
I took a numerical approach by solving in R.
I begin by making a list of all possible combinations of x, y, and z with the knowledge they can take any value in the set {1:9}. Then for every possible value of x, y, and z, I calculate the LHS: x x + y y + z z and RHS: x y z . Using MSE as the error function, I then find where the error is equal to zero. And the solution is 198, so the answer is 8 .
Note: MSE = ( ( x x + y y + z z ) − x y z ) 2
R code:
l <- list(x = 1:9, y = 1:9, z = 1:9)
w <- do.call(expand.grid, l) # all possible combinations
q <- matrix(0, nrow = 729, ncol = 3)
for (i in 1:729) {
u <- w[i, ]
x = as.numeric(u[1])
y = as.numeric(u[2])
z = as.numeric(u[3])
q[i, 1] = as.numeric(paste0(x, x)) + as.numeric(paste0(y, y)) + as.numeric(paste0(z, z)) # LHS
q[i, 2] = as.numeric(paste0(x, y, z)) # RHS
q[i, 3] = (q[i, 1] - q[i, 2])^2 # loss function
}
q[which(q[,3] == 0), ] # where there is no error
That's a great "modern" method!
First column says that X+Y=10. then easily Y=Z+1. And X+Z=9, the X in the third column must be 1. so, X=1, Y=9, Z=8.
so.11+99+88=198. so Z is the answer
nice solution.
Base on the figure, we can say that
x + y + z = 10 + z
x + y = 10 (1)
Since 1 is added to the tens place,
x + y + z + 1 = 10 + y
10 + z + 1 = 1 + y
z + 1 = y (2)
since the remainder 1 from x + y + z + 1 is equal to x,
x + y = 10x (3)
Then we have now three equations:
x + y = 10 (1)
z + 1 = y (2)
x + y = 10x (3)
And it is easy for us to get the solution. After we solve, we get:
x=1, y=9, z=8 or (1,9,8)
So, the value of z is equal to 8. 8 is the correct answer.
To check, 11+99+88=198, right?
XX+YY+ZZ = 11+99+88 = 198
Z=8
X could be at most 2. Writing the problem out substituting what I can, I begin with X=1, and Z as each of the given answer choices, with Y unknown initially. Quickly it is seen that in order for the Z in the sum to equal the Z addend, Y has to be 9, and, Z cannot equal 9. Only three attempts in, and the solution is found.
e.g.
11+YY+66 --> 11+99+66 = 176
11+YY+77 --> 11+99+77 = 187
11+YY+88 --> 11+99+88 = 198 = Answer
I made cases and cancel out the wrong ones one by one. 1. X can be 1 or 2, but 2 is possible only and only when all 3 digits are non eqaully more than 5 i.e., X should also be greater than 5, hence X can be "1" and not 2.
-
Choose Y in such an order that X + Y= 10, because only in this case adding Z will give Z at units place and 1 will go carry to tens place, which will satisfy my 3rd case. So this statement deduces that Y = 9.
-
Y = Z + 1, this statment can be seen by that when we are adding X, Y and Z in ones place, they are giving Z (obviously with a carry), so that carry is gonna sum to tens digit X, Y and Z and produce Y (with carry 1).Hence Z = 8
Its easy if you figure out the basic rule that y is z + 1 and that x must be equal to 1 or 2 as its maximum and minimum this means that y + x is equal to z this means it's equal to 8 or 9 however we can eliminate 8 as 2 + 8 + 9 is equal to 19 which makes it impossible for it to Equal 2 which means x is equal to 1 y is equal to 9 which leaves x as equalling 8 as y - 1 equals z as previously established we can test this through substituting 11 +88 +99 =189 There are probulary easier solutions but i like to over complicate problems(don't die reading it punctuation is terrible)
Being Z the first digit in the result necessitates that X+Y = 0 or 10 and as we know "each letter represents a different nonzero digit",SO (X+Y must equal 10 ) then on the other side X+Y+Z+1 must equal XY which means (11+Z = XY) trying different values for Z keeping in mind that X+Y must equal 10, we find Z must be 8 ...So XY = 19 which is X+Y = 1 +9 = 10 .
Just use hit and trial with some logic.JAI MATA DI
It's easy to see that X + Y = 1 0 and Z + 1 = Y ⇒ 1 ≤ Z ≤ 8 . ⇒ 1 1 ≤ X + Y + Z ≤ 1 8 ⇒ X = 1 ⇒ Y = 9 ⇒ Z = 8
- If you look at the digits column, X + Y + Z = A||Z therefore, X + Y = 10 . This means that the highest that X + Y can be is 19 and so looking at the tens column, Y must be 1 more than Z. Again, as the highest that X + Y can be is 19, X has to be 1. Therefore Y = 9 , substituting it in, 11 + 99 + Z||Z = 19||Z .
Therefore, Z has to equal 8.
My first observation was that z is both in the sum and the addends. This led me to believe the sum of x+y was 10. Next the logic was y was a result of regrouping a plus 1. Therefore Z+1= y. Using these observations I concluded x equal to 1. It followed that 9+1 =10. If y is one more than z, the z is 8. Concluding x y z is 198
Suppose that X, Y and Z were the maximum possible values, i.e. 9, 8 and 7. This give 99 + 88 + 77 = 264. Since X corresponds to the hundreds digit of the sum, X has to be less than or equal to 2. Now suppose that X = 2 and find the maximum possible sum i.e. 22 + 99 + 88 = 209. Since Y is a nonzero digit, X can't be 2 and therefore equals 1.
The above reduces the first column (of the sum) to 1 + Y + Z = 10 + Z. Solving for Y gives Y = 9.
The second column becomes 1 + 9 + Z + 1 = 19 (the additional 1 on the LHS is carried over from the sum of the first column), and solving for Z gives Z = 8.
We can see immediately that X=1 or X=2 (three 2-digit numbers can't sum to 300), and that X+Y=10. Hence, we either have (X, Y) as (1, 9) or (2, 8).
(1, 9) gives 1+1+9+Z=19 from the left-hand column - remembering to include the 1 carried from the right-hand column - so Z=8.
(2, 8) gives 1+2+8+Z=28 - this cannot be the case since it would mean Z=17.
Units place column shows.
x+y = 10.
We also have.
100x+10y+z=11x+11y+11z.
Or 89x = y +10z=10-x+10z.
Or 90x = 10 + 10z.
Or 9x = 1 + z,
As 1 + z is less than or equal to 10,.
9x can only be 9, so 1 + z = 9.
=> z = 8.
Since X + Y + Z = Z plus a carrier (this carrier can only be one* ), and X +Y + Z = Y as the first digit, X = 1 **. and Y = Z + 1. so : 1 + Z + 1 + Z = Z plus carrier --> Z = 8 since 1 + 8 + 1 + 8 = 18 which has 8 as the first digit.
*the carrier is one because of this:
- it can be zero but that is impossible since the same three digits amount to different result in the two columns.
- it can be two at maximum (9+8+7 = 24) but that its also impossible cause if it had two as a carrier, that means the result will be one of (20, 21, 22, 23, 24) so y will be one of (0, 1, 2, 3, 4) but even for the max value of y = 4 and x = 3 at max, we can have z to amount to 24.
** X= 1 because of two things: - it is the carrier of the second step and it is the same as the first step since the sum of the first (X+Y+Z) cannot have 9 as the first digit because of the same previous argument in *
10x+x+10y+y+10z+z=100x+10y+z;
x+y must equal 10 so that z+0=z;
10x+10+10z=100x;
10+10z=90x;
10(z+1)=90x;
z+1=9x; z=9x-1;
We want (9x-1) to be a digit.
This only happens when x=1.
So z=8.
The first column shows that x+y=10 so that x+y+z=z+10. You carry the one and x+y+z+1=y+10 which means that y=z+1. Given these restrictions, it seems incredibly unlikely that x is anything other than 1 because the three digit number would be too large. Plugging in 1 for x and filling in the rest of the variables gives us a possible result so x=1, y=9, and z=8.
1 1 X + 1 1 Y + 1 1 Z = 1 0 0 X + 1 0 Y + Z ⇒ 1 0 Z + Y = 8 9 X ⟹ 1 0 Z = 8 9 X − Y
Therefore,
8 9 X − Y ∈ { 8 9 X − 9 , … , 8 9 X − 1 } ∩ { 1 0 , 2 0 , … , 9 0 }
But:
{ if X = 1 , then { 8 9 X − 9 , … , 8 9 X − 1 } ∩ { 1 0 , 2 0 , … , 9 0 } = { 8 0 , … , 8 8 } ∩ { 1 0 , 2 0 , … , 9 0 } = { 8 0 } if X ∈ [ [ 2 , 1 0 ] ] , then { 8 9 X − 9 , … , 8 9 X − 1 } ∩ { 1 0 , 2 0 , … , 9 0 } = ∅
Hence
X = 1
thus (with 1 0 Z = 8 9 X − Y and Y , Z ∈ [ [ 1 , 9 ] ] ):
Y = 9 and Z = 8
I first figured out the constraints and knew that XYZ was between 132 and 264, which meant that X either had to be a 1 or 2. Since you're going to be carrying over from the first column, the value of y was going to be one more than the value of z. Some guessing from there with those parameters got me 1,9 and 8.
X + Y = 10 (only way that X + Y + Z = Z from first column, where X & Y are different nonzero)
X + Z = 9 (only way that X + Y + Z + 1 = Y from second column, where we know a one was carried from the first column)
X = 1 (because Z < 10 and X +Y + Z + 1 = Y from second column, so X + Y + Z + 1 is less than 20, but greater than 10)
Therefore, Z = 8 from second equation (and Y = 9 from first equation):
11
99
+ 88
-----
198
From the equation, we know that x+y+z=xy-1>10 and x=1
Since we know that 1+y+z=1y-1 then the only possible number for z is 8
I used the fact that X X , Y Y , and Z Z are multiples of 11 to solve this one real fast!
1 1 X + 1 1 Y + 1 1 Z Y + 1 0 Z = ⇓ = 1 0 0 X + 1 0 Y + Z 8 9 X
Therefore, X must be equal to 1. Why? Because we know that X , Y , and Z are non-zero digits, meaning that they are whole numbers greater than 0 and less than 10. Therefore, X cannot be >1 because the largest the left side of the equation above can be is 99 (or 98 if the digits have to all be different). Now we know that:
Y + 1 0 Z = 8 9
Using similar reasoning, because Y cannot be greater than 9, 1 0 Z must be greater than or equal to 80. Therefore, we know that Y must equal 9 and Z = 8