77 of 100: Flip Efficiently!
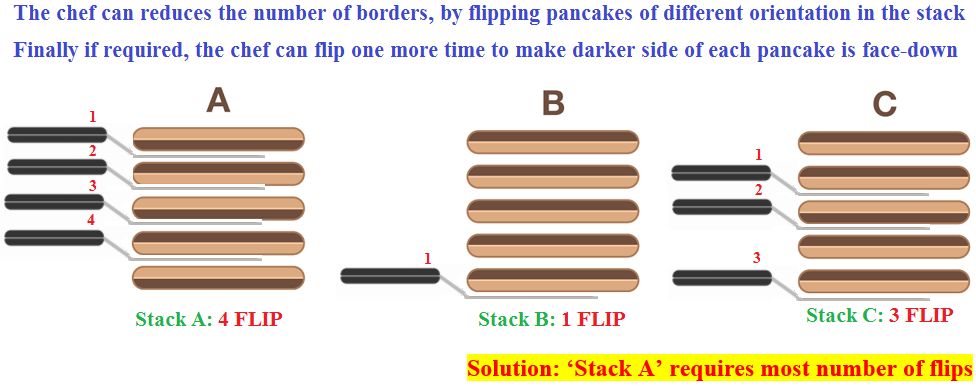
A chef wants to flip all of the pancakes in a 5-pancake stack so that the darker side of each pancake is face-down. The chef uses a series of flips, where at each flip the chef inserts a spatula and simultaneously flips all the pancakes above it.
If the chef flips each stack in the most efficient way possible, which one of these three stacks of pancakes requires the most flips?
Note that a flip reverses the top-to-bottom ordering of the group of flipped pancakes, as well as the orientation of each pancake. The animation is just for illustration of the stack-flipping process; the stack shown isn't related to the answer choices.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Solving the problem can be hard, but generalising it is far more challenging. Great job on this, clever and clear, was a pleasure to read this!
Wonderfully clear generalization! I agree, this was a pleasure to read.
Stack B
Flip it from below.
Only 1 flip is needed.
Stack C
Flip it from below.
Then, flip the first two cakes.
Finally, flip the first three cakes.
Only 3 flips are needed.
Stack A
Flip the first three cakes.
Then, flip the first one.
Then, flip the first two cakes.
And, then flip the first four cakes.
4 flips are needed in this case.
Great One Bro!
The clearest one to me
For Stack A:
There are many ways, I did it this way: (Considering the naming convention i am using is the side which is currently facing downward) D L D L D − > L D L D L − > D L D L L − > L D L L L − > D L L L L − > L L L L L − > D D D D D (6 steps)
(Flip from bottom most pancake then in serial order flip the one above and so on)
For Stack B: Just Flip from bottom
L L L L L − > D D D D D (One Step)
For Stack C L L D L L − > D D L L L − > L L L L L − > D D D D D ((3 Steps)
If two pancakes have the opposite orientation, you need to flip one but not the other. Or in other words, you need to flip between them. Thus the stack needing the most flips is the one where they alternate
this solution set you free from rotations.
let's check from bottom to top, if the cake one is correct, we will leave it alone, if it's not correct we will flip it take Set A as example,
let's image the top one is called 'e' and the bottom one is called 'a'.
a is correct, we leave it alone, and check b...... b is incorrect, we flip [ flip 1]...... c is correct at beginning, but after [ flip 1] it become incorrect, we flip [flip 2]...... d is incorrect at beginning, after [ flip 1] [ flip 2], it's still incorrect, we flip [ flip 3]...... e is correct at beginning, after [ flip 1] [ flip 2][ flip ], t's still incorrect, we flip [ flip 4]......
same logic also applicable to set B and set C
Special Theory of Flippancy - a stack of pancakes may be modeled by a binary number as follows, a down pancake is a 0 and an up pancake is a 1. The least significant bit is at the top of the stack. Therefore, STACK A is modeled as 01010, and STACK B as 11111, and STACK C as 11011. The goal in this task is to get to 00000 by flipping bits.
General Theory of Flippancy - in this solution, the spatula "^" operator flips the bits AND reverses the order of all of the bits to the right of it, in a binary number. As an example, for STACK B, the operation ^11111 results in a new stack of 00000. The spatula "^" operator changes the decimal parity of a number from odd to even, or from even to odd.
For STACK C, three operations are required. Why? Well, the stack has odd decimal parity because binary 11011 equals decimal 27, which requires an odd number of "^" operations to turn it into a stack with even parity but more importantly STACK C has FLIPPANCY = 3. FLIPPANCY is determined by reading the binary number from right to left. If the rightmost bit is 0, the FLIPPANCY starts at 0 and if the rightmost bit is 1 then the FLIPPANCY starts at 1. The FLIPPANCY increases by 1 each time the next more significant bit "flips" compared to the previous bit. Going back to STACK B equal to 11111, note that its parity is odd (i.e. a solution would require an odd number of flips) and that its FLIPPANCY is 1, since 1 is its rightmost bit and none of the successive bits are "flipped". For STACK C equal to 11011, its FLIPPANCY is 3 and may be solved by a minimum of 3 "^" operations. You could use 5 or 7 or any odd number of operations, but 3 is the least number needed. An example could be 110^11 => 11000, 11^000 => 11111, and finally ^11111 => 00000.
STACK A equal to 01010 has even decimal parity (i.e. binary 01010 equals decimal 10) which means that a solution will require an even number of "^" operations. More importantly, 01010 has FLIPPANCY equal to 4, so it could be solved by the (minimum) series of operations: 0101^0 => 01011, 010^11 => 01000, 01^000 => 01111 and finally 0^1111 => 00000. Other sequences of operations can also reduce this stack to 00000 but any solution will require an even number of operations, greater than or equal to 4.
Note, this task was simple enough that a theory of FLIPPANCY was not needed but in a more complicated problem, let's say a hungry person stack of 12 pancakes, a theory of FLIPPANCY could be very useful. Chow?
This was like reverse psychology...when you're cooking pancakes why would you ever flip them to further cook the darker side!?
You put the dark side down so your wife doesn't see that you burned them.
The number of flips seems to be related to the changes in orientations of adjacent pancakes which is 4 in A, 0 in B and 2 in C. The number of flips is 4 in A, 1 in B and 3 in C. In case of n pancakes, if x is the number of orientation changes, the number of flips = x + 1 with a minimum of 1 and a maximum of n.
In B, all of them are wrong. So a single flip will give the desired result.
In C, the first flip yields (from top to bottom) RRWRR (R - Right W - Wrong). So we flip about the 2nd pancake from the top to get WWWRR and then flip about the third pancake from the top to get RRRRR
In A, the bottom most pancake is in the right position. It can be seen that flipping about the 2nd pancake from bottom or 4th pancake from top will yield the same configuration and hence is pointless. Flipping about the 3rd pancake from top we get (again from top to bottom) WRWW R . Flipping the top most pancake, we get RRWW R , Then flipping about the 2nd pancake from top we get WWWW R. Now flipping about the 2nd pancake from bottom , we get RRRRR making a total of 4 flips
Generalization : Start with "face-down" and list the pancakes from bottom to top. Count how many "inversions" take place, i.e. how often you go from "face-down" to "face-up" and vice versa. This number of inversions ( Q ) is the required number of flips.
Application : Here d and u stand for face-down and face-up, and the vertical bars represent inversions.
stack A: ( d ) d ∣ u ∣ d ∣ u ∣ d ; Q = 4 .
stack B: ( d ) ∣ u u u u u ; Q = 1 .
stack C: ( d ) ∣ u u ∣ d ∣ u u ; Q = 3 .
Strategy : Always insert the spatula at the top-most inversion, i.e. between the highest two pancakes with opposite orientation. This will reduce the number of inversions Q by one.
For instance, with stack A we perform:
( d ) d ∣ u ∣ d ∣ u ∣ ∣ d ↦ ( d ) d ∣ u ∣ d ∣ ∣ u u ↦ ( d ) d ∣ u ∣ ∣ d d d ↦ ( d ) d ∣ ∣ u u u u ↦ ( d ) d d d d d .
Proof that this works:
There is no faster way. Below the spatula no changes take place, and the number of inversions there remains unchanged. Above the spatula, all pancakes change orientation and order; all inversions remain intact, but in opposite order. At best, one inversion may be removed, namely at the place of the spatula.
This way does the job. Let a be the pancake just below the spatula, b the pancake just above it, and c the pancake on top. Flipping results in ⋯ a ∣ ∣ b ⋯ c ↦ ⋯ a c ˉ ⋯ b ˉ . Since we inserted the spatula at the last inversion, all pancakes b ⋯ c have the same orientation, so that c = b . Since we inserted the spatula at an inversion, we know that b = a ˉ . Combining this, we find that c = a ˉ . After flipping, the pancakes around the spatula are a = c ˉ : we have removed an inversion!
Note : Often there are multiple ways to accomplish the minimum number of flips. In general, we may flip at an inversion, provided that an even number of inversions lie above the spatula. Or, the pancake just above the spatula should
have the opposite orientation of the pancake just below the spatula; and
have the same orientation as the pancake on top.
Any other flip will make it impossible to attain the minimum number of flips!