79 of 100: Guards in the Gallery
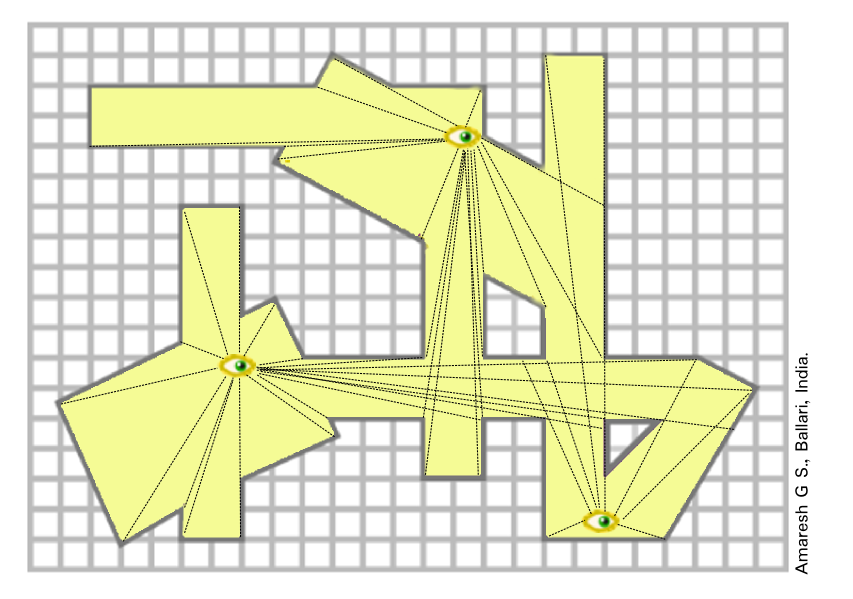
The purple figure below is the floor plan of a gallery, and an example is shown of what could be seen by a single guard who cannot see through walls but who can look around.
Your job is to position some number of guards in the gallery such that every location in this gallery is in view of at least one of the guards.
What is the fewest number of guards that you can use to guard the entire gallery?
Make sure every nook and cranny is visible to at least one guard! You can assume any sub-region of the gallery that appears to be a rectangle is, in fact, a rectangle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The floor plan can be divided into eight simple shapes (rectangles, and one near-rectangle in the southeast corner). Each of these shapes is convex ; this implies that, for any two points P and Q in the shape, the line segment P Q lies entirely within the shape; that is, a guard standing at any point P is able to see every point Q without obstruction.
To cover the entire gallery, we just need to make sure that each of the eight shapes has (at least) one guard; to minimize the number of guards, we place them as much as possible in the overlap of the shapes. The diagram below shows how this can be accomplished with three guards: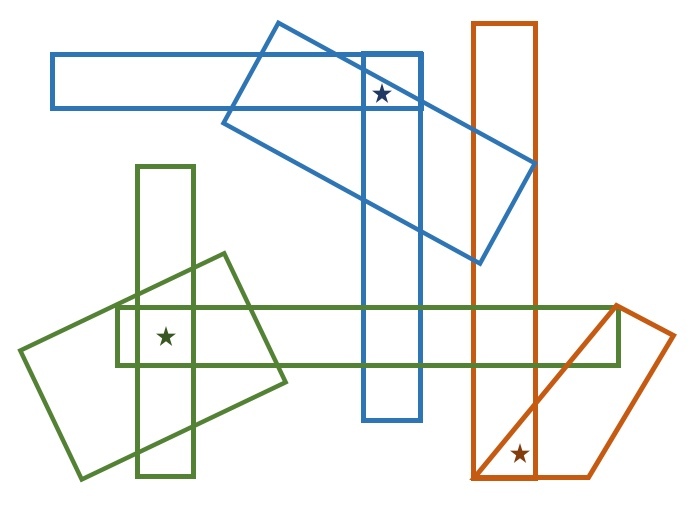
For a complete proof, we must make sure that there is no solution with less than three guards. This is easy to see. Consider the "dead-ends" of the three hallways running north-south. In order to cover such a dead end, a guard must be somewhere inside the rectangle belonging to that hallway. Since the three rectangles do not overlap, this requires at least three distinct guards.