8 of 100: The Most Efficient Cuts
What is the least number of cuts that must be made in order to completely cut through this rope fence? Note: The knots where multiple ropes meet are too thick to cut through.
This puzzle can be solved intuitively and with trial-and-error, but there's also a beautiful result from graph theory, the Max-Flow Min-Cut Algorithm , that can be used to both solve this puzzle and to quickly prove the solution optimal. Use the link to learn how the result applies!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
If we cut the rope at intersections, can't we do it with just three cuts?
Log in to reply
I missed that comment too. I wish it was listed as part of the problem, not as an addendum. I too found the answer to be 3, so I picked 4.
Log in to reply
Thanks for the feedback -- I've moved it up, so that it's immediately after the problem statement! :)
Read the bolded note to the question: you are not allowed to cut at knots!
Cool 😎 interactive picture.
Exactly right. Good explanation.
I got the question correct using this method, but can't we just do one big cut that goes through these 5 horizontal lines? The question is still not very clear. Maybe specify that you can only cut one rope at a time? I was always confused at exactly what you were asking for.
For student purposes, please consider placing "bold information" that is necessary to answer the problem within the context of the problem in the future, not so far below it. When seeing the problem on the site with advertisements, difficulty level, etc, students are easily missing the NOTE. This creates frustration for them when they get problems incorrect due to missed information and therefore will not continue with the challenge. Thank you!
Log in to reply
Well said as it frustrated this teacher who got it wrong for that reason!
Maria, thank you for the feedback! I've moved that line up so that it's immediately after the problem statement and still in bold.
This is such a simple solution!
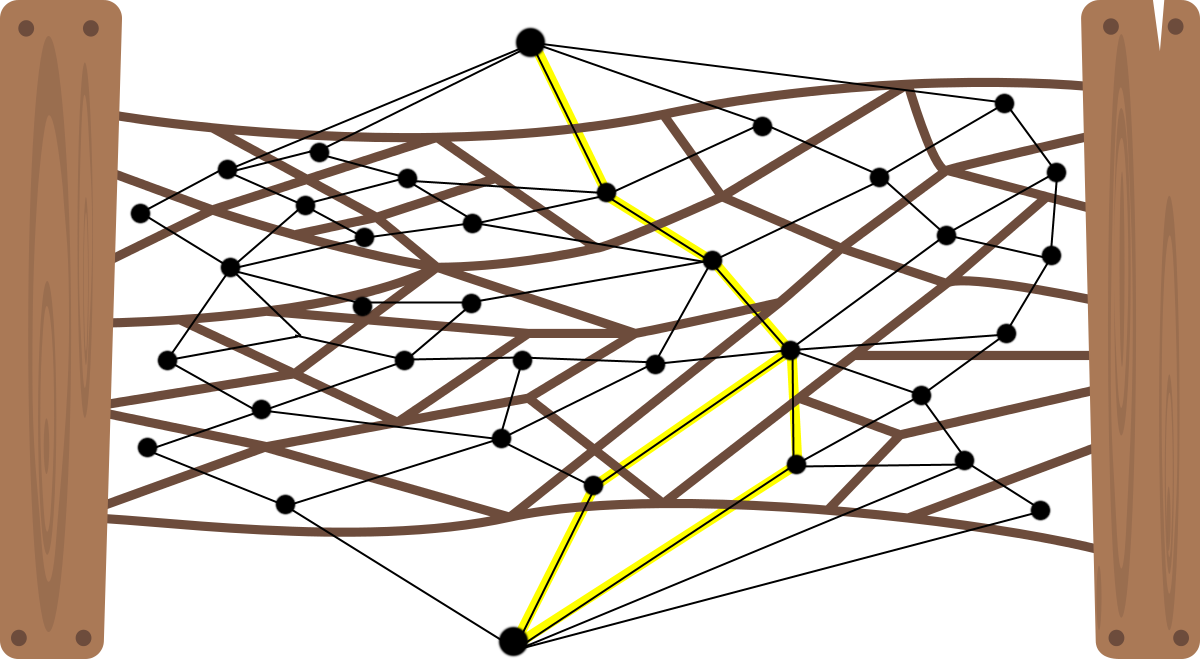
Construct its dual graph (the faces turn into vertices and the edges into their corresponding dual edge), then find the shortest path between the top and the bottom (through breadth-first search ). The edges of that path will correspond to the edges to cut, and for this fence the answer is 5
:D Very awesome.
I used the same idea to solve the problem but I lack the mathematical knowledge to express it in graph, with nodes and paths. Now I learnt something. :D
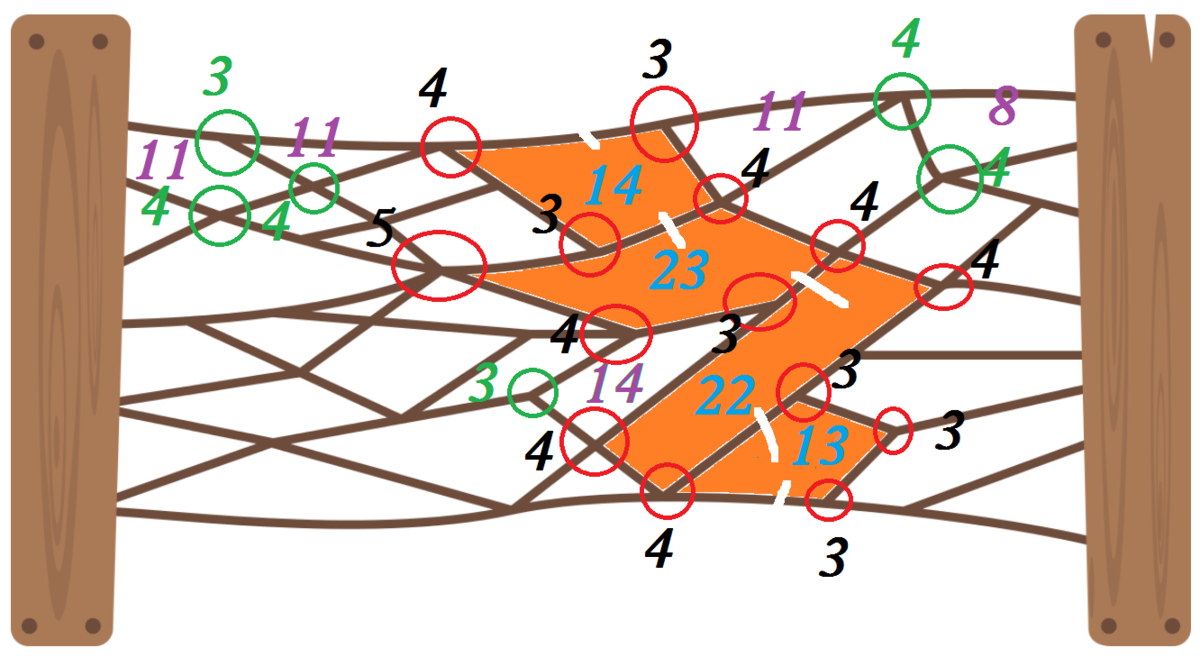
Cut the ropes where there are the most connected nodes for a cell, and cut from one 'most connected' cell to the next adjacent 'most connected' cell.
Hmmm.... Can you explain the what the numbers in the diagram mean (e.g., 23, 22, 3,4, etc.)? Not getting that.
Log in to reply
The sum of the nodes for that cell, red circles are the sum of the nodes. Number in purple are cells with lower node count, cells with number in blue are high node count. From top to bottom, summing nodes each cell clockwise 14 = 4+3+4+3; 23=5+3+4+4+3+4; 22=4+3+4+4+3+4; 13=4+3+3+3. 4 cells, 4+1 cuts, 5 cuts is the smallest number.
at first 14 cell every rope works fine? (connects 4 with 3) the same problem also with the rest
Answer is 4 when the knot is cut finally.
Log in to reply
You cant cut the knots, it is said in the note. If you cuold cut the knots you can solve the problem with 3 cuts.
I searched for the minimum number of areas linked by a line to be crossed from top to bottom to reach the other side.
I found the minimum areas to cross are 4, in two different pattern for the last one.
The last step was simply to cut the way with 5 cuts.
Cutting at the intersections, I was able to find a place to do it in 3.
Log in to reply
You cant cut the knots, it is written in the probelm's note in bold text.
I could do it in 4. If you cut at the intersections of the rope it is possible to do with 4 cuts.
Log in to reply
Cutting the knots you can do it in 3 cuts, but it is forbidden by the problem's note in bold text.
Finding 5 places to cut so that the fence is severed is only half of a solution -- in order to really know that 5 is the correct answer, you somehow have to prove that it's impossible to sever the fence in four or fewer cuts.
This solution and proof is a small example of the Max-Flow Min-Cut Algorithm , a beautiful duality in graph theory and linear programming!
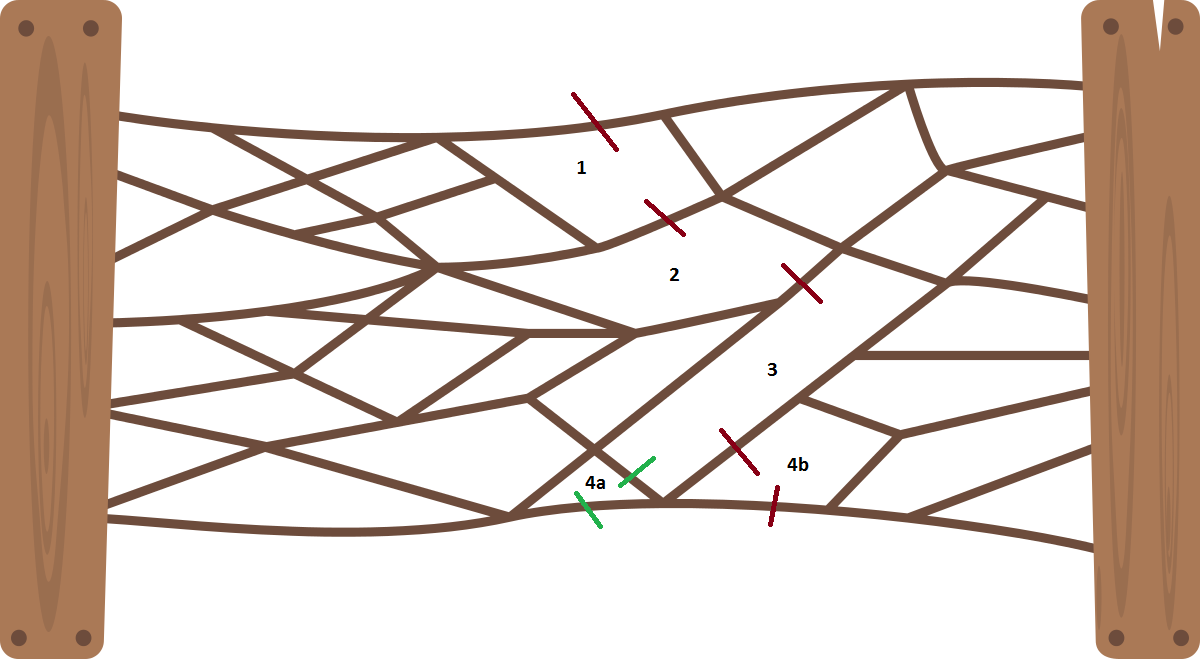
Here's an illustration of the strategy that "Max-Flow Min-Cut" enables: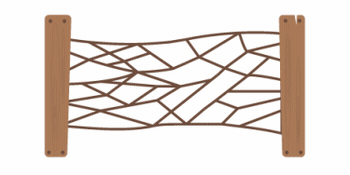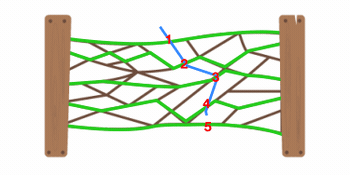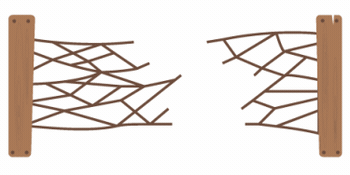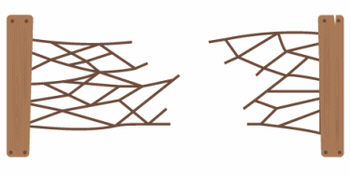
How it works:
Instead of guessing rope-segments to cut, draw in a set of horizontal paths that connect the two posts. Try to draw as many horizontal lines as possible without ever reusing a length of rope (though you can reuse an intersection). Wiggle around and refine your lines as needed to fit in as many as possible. This is called the "Max-flow" perspective, and that terminology hints at a different interpretation of the situation: If each of these ropes were instead a hose with a flow capacity of 1cm of water/second, how much water-per-second could be pumped from the left side of the system to the right side?
Because it's possible to draw in 5 distinct, horizontal lines, we can conclude that 5 cuts are not just sufficient but necessary in order to sever the fence. In order to sever the fence, we have to cut across at least one segment in each green path. So, this 'max-flow' diagram of 5 distinct, horizontal green lines serves as a proof that the fence cannot be severed in four or fewer cuts!
The 5 cuts illustrated above work! And now we've also proven that least 5 cuts are necessary. QED!