83 of 100: Broken Red Circle
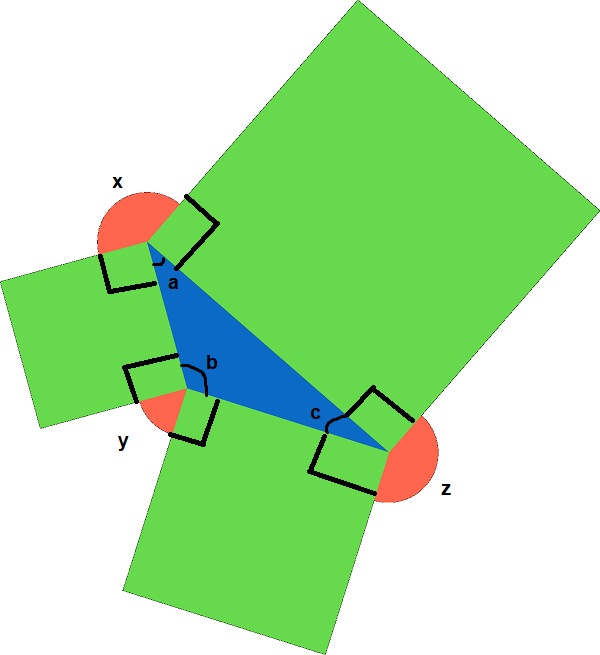
Three squares are added to the sides of a triangle as shown. Is the following statement true or false?
"The sum of the three red angles will always equal 3 6 0 ∘ regardless of the type of triangle drawn."
Bonus: Can you find a set of angles whose sum is 7 2 0 ∘ ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
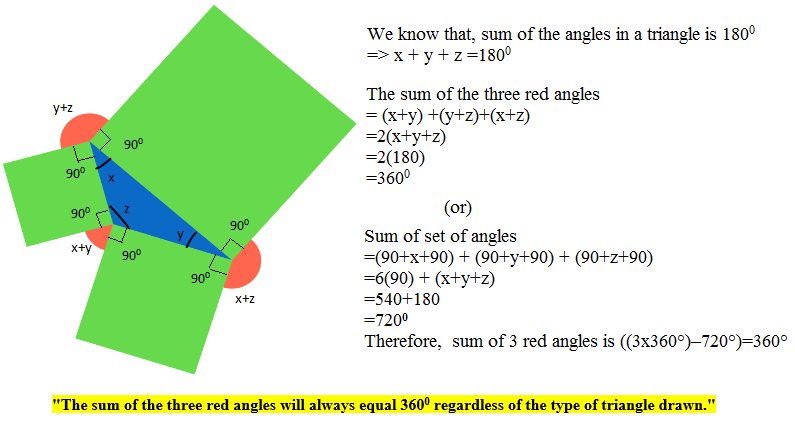
That is a nice algebraic way to show that each of the red angles is the supplement of the corresponding angle in the triangle, thus equal to the sum of the two remote interior angles. These 3 sets of 180° each, less the triangle's 180°, yields 360°.
Very nice proof.
Cut two of the red sectors out and slide them (without rotation) toward the third. They will fit together and form a full angle of
3
6
0
∘
. This is guaranteed to work because opposite sides of squares are parallel to each other. (Yes, you could do this problem with any parallelograms instead of squares!)
For the bonus part:
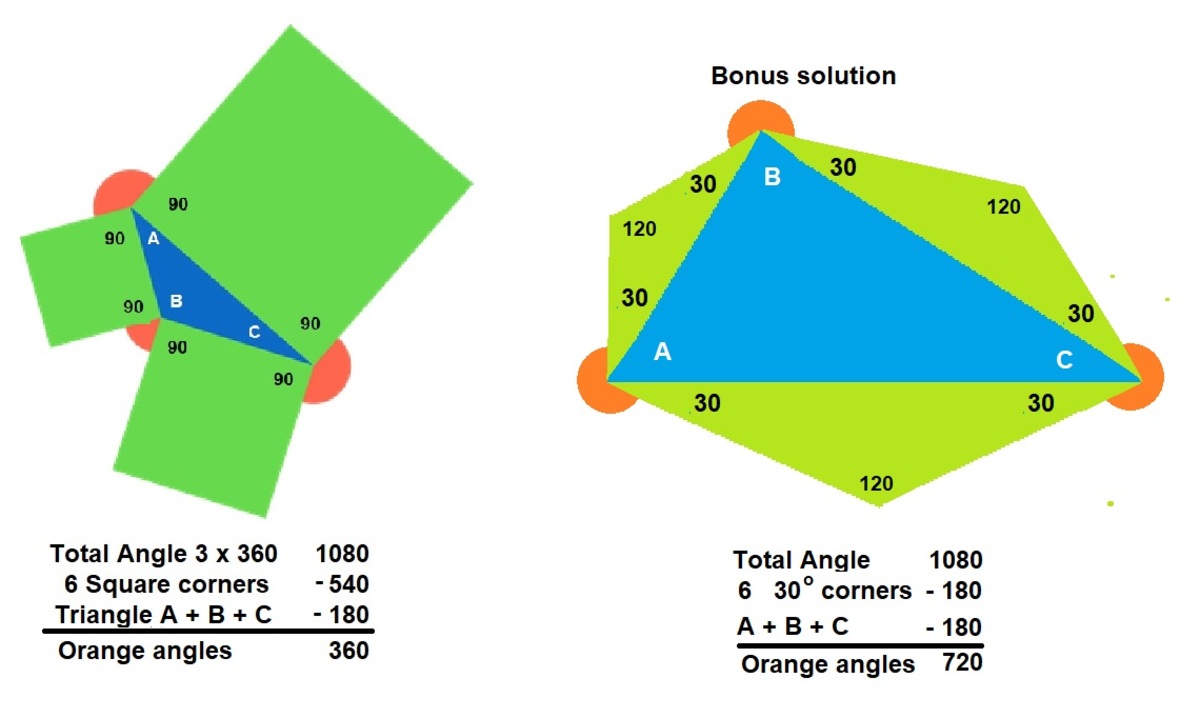
If we replace the squares with isosceles triangles having angles ( 1 2 0 ∘ , 3 0 ∘ , 3 0 ∘ ), then we'll get outer angles adding up to 7 2 0 ∘ . But, this time the solution is correct for triangles only!
I love this proof, it works for any convex polygon and could be animated beautifully by just shrinking the triangle down to nothing. I suppose it works for non-convex too but not in such an intuitive way as it involves negative angles.
The angle around each of the 3 vertices of the triangle is 360°.
So, the total sum of the angles around 3 vertices=(3×360°)=1080°.
So, from each of the 3 squares we get 2 right angles around each of the 3 vertices.
And the sum of 3 angles of the triangle is 180°.
So, from the triangle and the squares, we get (180°+(6×90°))=720°.
Hence, the sum of 3 red angles is (1080°–720°)=360°.
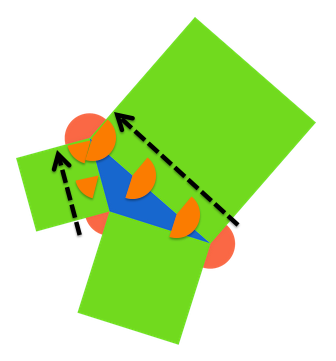
Imagine walking counterclockwise along the edges of the triangle with your right arm sticking out. As you complete the tour, your right arm aligns with the perpendicular edges of the squares at each vertex. That arm will sweep over the red sectors, completing 3 6 0 ∘ of a circle as you go around once (just imagine that you skip the forward motion).
This is the best intuitive explanation, by far!
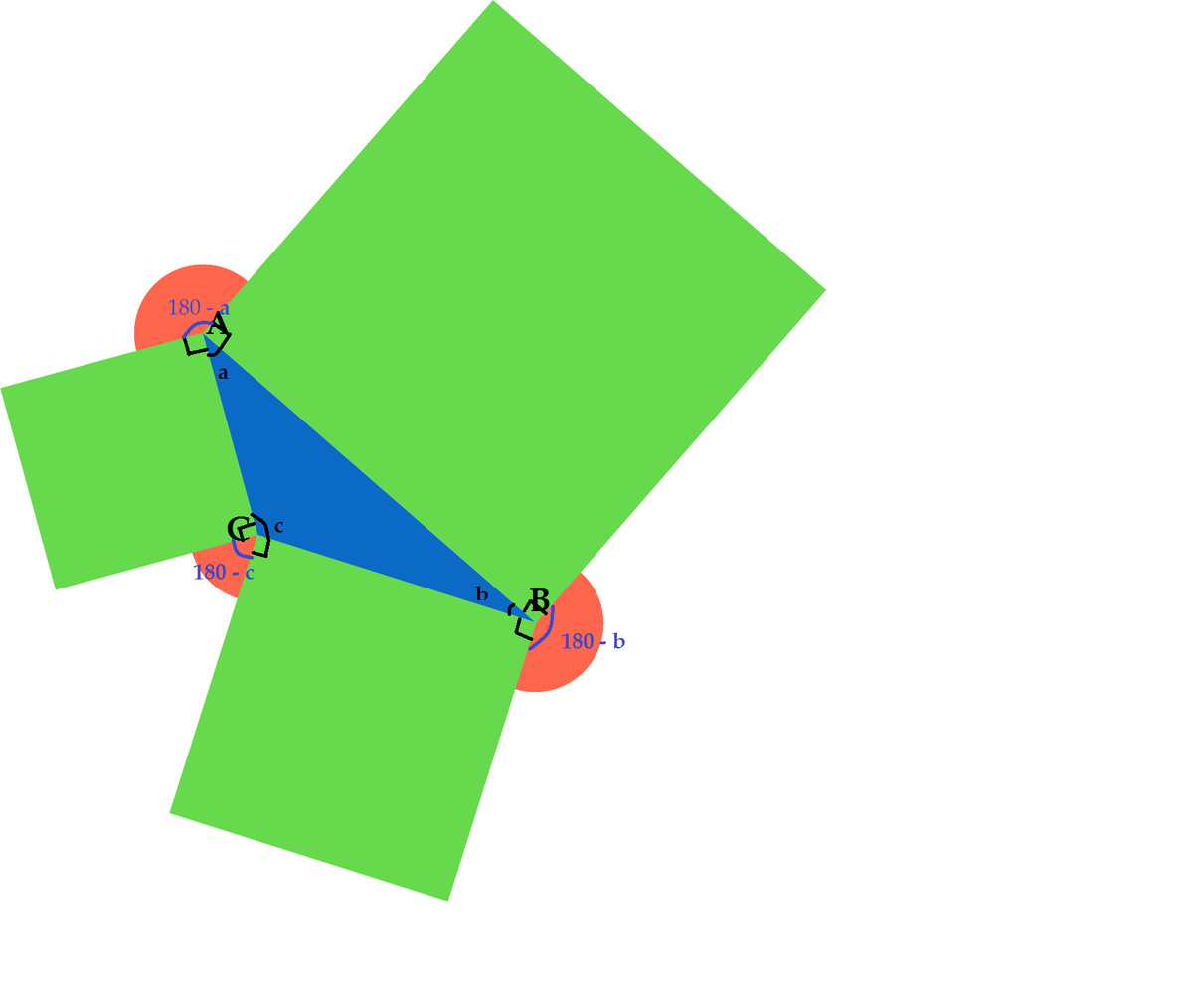 a
+
b
+
c
= 180
a
+
b
+
c
= 180
540 - 180 = 360
Let's say the three red angles have values x, y, and z respectively. We want to prove x+y+z = 360. Now let's say that the three angles in the triangle are a, b, and c respectively. We know that a+b+c = 180. We can also create the following three equations based off of the diagram and the given information: x = 360 - 90 - a - 90 = 360 - 180 - a = 180 - a y = 360 - 90 - b - 90 = 360 - 180 - b = 180 - b z = 360 - 90 - c - 90 = 360 - 180 - c = 180 - c We will now use these three equations to rewrite the sum x +y +z: x + y + z = 180 - a + 180 - b + 180 - c = 540 - (a+b+c) = 540-180 = 360. Thus, the answer is true .
 Angles in a circle add to 360. Since there is a square on either side of each angle in the triangle (adding up to 180 degrees), a red angle is equal to 180 - the corresponding triangle angle.
Angles in a circle add to 360. Since there is a square on either side of each angle in the triangle (adding up to 180 degrees), a red angle is equal to 180 - the corresponding triangle angle.
Thus, the sum of all the red angles is 3(180) - (x+y+z).
We also know that x+y+z =180.
Therefore the red angles sum to 3(180) - 180, which is 360, regardless of the sizes of x,y and z.
Let the vertices of the blue triangle be A , B and C . Then,
The sum of 3 red angles = 3 × angle around a point (vertex) − 3 × 2 green right angle − ( ∠ A + ∠ B + ∠ C ) = 3 × 3 6 0 ∘ − 3 × 2 × 9 0 ∘ − 1 8 0 ∘ = 3 6 0 ∘
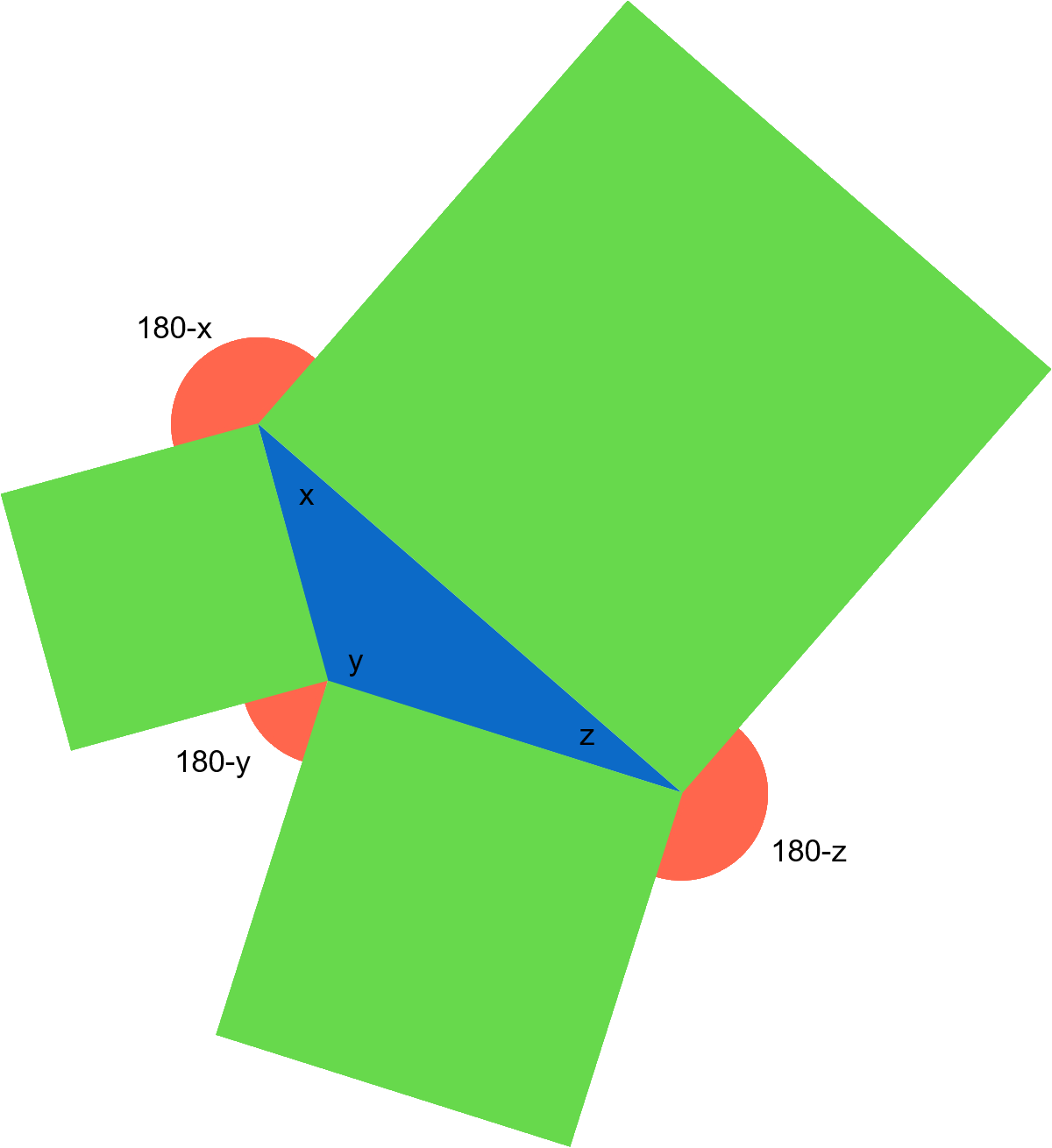
Call each of the angles in the triangle x, y & z. (Note: x + y + z = 180 - sum of angles in a triangle)
Work out the exterior angles (orange);
Sum of angles around a point = 360
Angle 1 : 360 - (90 + 90 + x) = 180 -x
Angle 2 : 180 -y
Angle 3 : 180 - z
Sum the angles : 180 + 180 + 180 - x - y - z = 180 + 180 + 180 - (x + y + z) = 180 + 180 + 180 -180 = 360
Notice that a + 9 0 + 9 0 + x = 3 6 0 , b + 9 0 + 9 0 + y = 3 6 0 and c + 9 0 + 9 0 + z = 3 6 0 . Then we have these equations:
a + x = 1 8 0
b + y = 1 8 0
c + z = 1 8 0
Summing then up:
a + b + c + x + y + z = 5 4 0
Since the sum of internal angles of any triangle is 180 degrees we have 1 8 0 + x + y + z = 5 4 0 . Then we conclude that x + y + z = 3 6 0 .
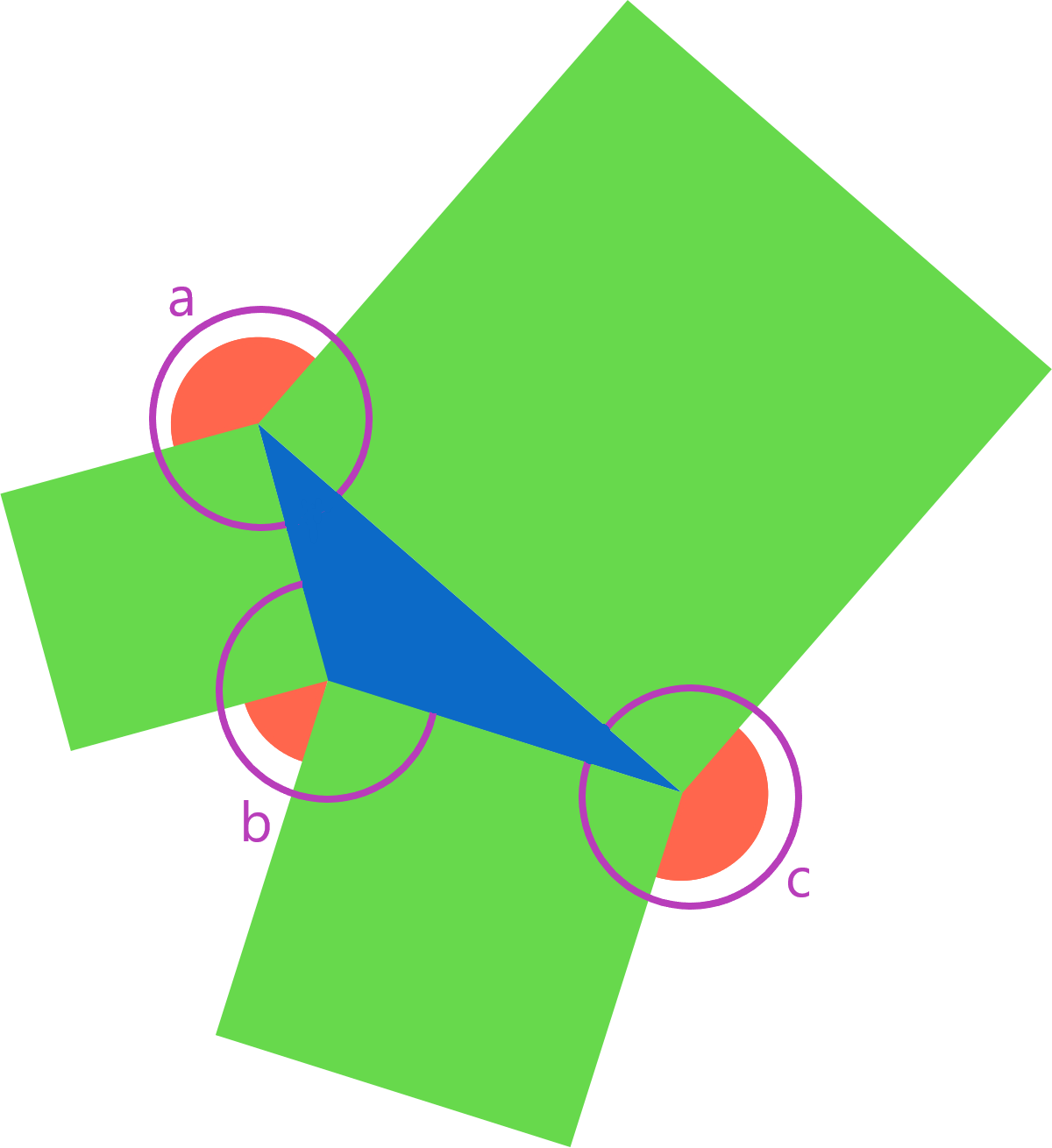
Call the three vertices of the triangle: ptA, ptB and ptC.
At each vertex there are 4 angles: the interior angle of the triangle, x, the red angle outside of the triangle, X and the right angles of two squares. These four angles add up to 360 degrees and therefore (x + X) = 180 (at each vertex).
(a + A) + (b + B) + (c + C) = 540 degrees. However (a + b + c) = 180 degrees (i.e. interior angle sum of triangles). Therefore, (A + B + C), the sum of the red angles always equals 360 degrees.
Bonus: Can you find a set of angles whose sum is 720 degrees? I honestly did not know how to interpret that request, so I interpreted it like this: can you find a shape (i.e. not a triangle) where the "red angles" would sum to 720 degrees? For a triangle that sum is 360 degrees. Well, it turns out that the sum of the red angles is always 360 degrees for any convex polygon with squares drawn on its sides. Back to the drawing board ... for the given problem, a set of angles that always sums to 720 degrees is the three angles at each vertex excluding the red angles (i.e. x + 90 + 90). Hence (a + 90 + 90) + (b + 90 + 90) + (c + 90 + 90) = (a + b + c) + 540 which will always add up to 720 degrees, no matter what shape the triangle has.
Let the upper orange angle be x, middle orange angle be y, and the bottom orange angle be z
degrees. Also let the angles of the triangle in that order, be, r, s, t degrees. Then it is obvious,
x = 180 – r, y = 180 – s, and z = 180 – t degrees. Since we have r + s + t = 180 degrees, it follows,
that, x + y + z = 360 degrees.
Let t 1, t 2, t 3 be the triangle angles, and r 1, r 2, r 3 be the associated red angles opposite the corresponding triangle angles. The sum of the 4 angles around each triangle vertex = 360 degrees = t_ I + r_ I + 90 + 90. Adding these 3 equations, t 1 + t 2 + t 3 + r 1 + r 2 + r 3 + 3(90 + 90) = 3*360 = 1080, or r 1 + r 2 + r 3 = 1080 - 540 - (t 1 + t 2 + t 3). But t 1 + t 2 + t 3 = 180, so r 1 + r 2 + r 3 = 1080 -540 - 180 = 360. Ed Gray
at every point sum of angles is 360 and consist of 2*90(angles of squares ) Ie sum of red angle and corresponding angle is 180 hence outer angle can be writen as 180-∆( angle of the triangle ) 3 times same thing gives sum of red circles =180
Total angle for three points = 3 x 360 = 6 x 180.. The total angle of the six square corners is always 6x90 = 3x180. The total angle of the triangle corners is always 1 x180. Angle remaining for the circular bits is 6 x 180 - 3 x 180 - 1 x 180 = 2 x 180 = 360.
One cactus.
To get 720 start with 1080 = 3 x 260. Deduct the triangle.to leave 900. Deduct the 720 goal angle to leave 180. Whatever figure is constructed on the sides of the triangle must have six corners that sum to 180. The most regular way to do that is for each corner to have 180/6 = 30 degrees of angle. This can be accomplished with three isosceles triangles with base angles of 30 degrees with their bases on the sides of the given triangle. These triangles fit easily into the area of the squares of the original problem and present no additional difficulties in spacial arrangement.
We know that the internal angles of a triangle always add up to
1
8
0
∘
, so therefore the external angles (abc) of the triangle must add up to
(
3
6
0
∘
∗
3
)
−
1
8
0
∘
=
9
0
0
∘
 The sectors of red must then equal
(
9
0
0
∘
−
(
9
0
∘
∗
6
)
=
3
6
0
∘
because there are six right angles from the squares removed.
The sectors of red must then equal
(
9
0
0
∘
−
(
9
0
∘
∗
6
)
=
3
6
0
∘
because there are six right angles from the squares removed.
The angle degree around each point is 3 6 0 o . Since there are 3 points in the triangle, we multiply by three to get 3 6 0 o ⋅ 3 = 1 0 8 0 o . Each point is also a vertex of 2 squares. We know that each vertex of a square has 9 0 o . So we subtract 2 ⋅ 3 ⋅ 9 0 o from the total to get 1 0 8 0 o − 5 4 0 o = 5 4 0 o . We know the sum of the interior angles of any triangle is 1 8 0 o , so we subtract this to get the sum of the red angles: 5 4 0 o − 1 8 0 o = 3 6 0 o
Say three red angles are A,B,C and angles of the triangle are E,F,G.
Now it is obvious that
A+G=360-180=180
B+F=360-180=180
C+E=360-180=180
Again A+B+C=180
Therefore E+F+G=180
There are three vertices, each with a full circle of 3 6 0 ∘ of space around it.
Total 3 6 0 ∘ × 3 = 1 0 8 0 ∘
Out of that the internal angles of the triangle will take 1 8 0 ∘
The six right angles will take 9 0 ∘ × 6 = 5 4 0 ∘
So what's left is 1 0 8 0 ∘ − 1 8 0 ∘ − 5 4 0 ∘ = 3 6 0 ∘
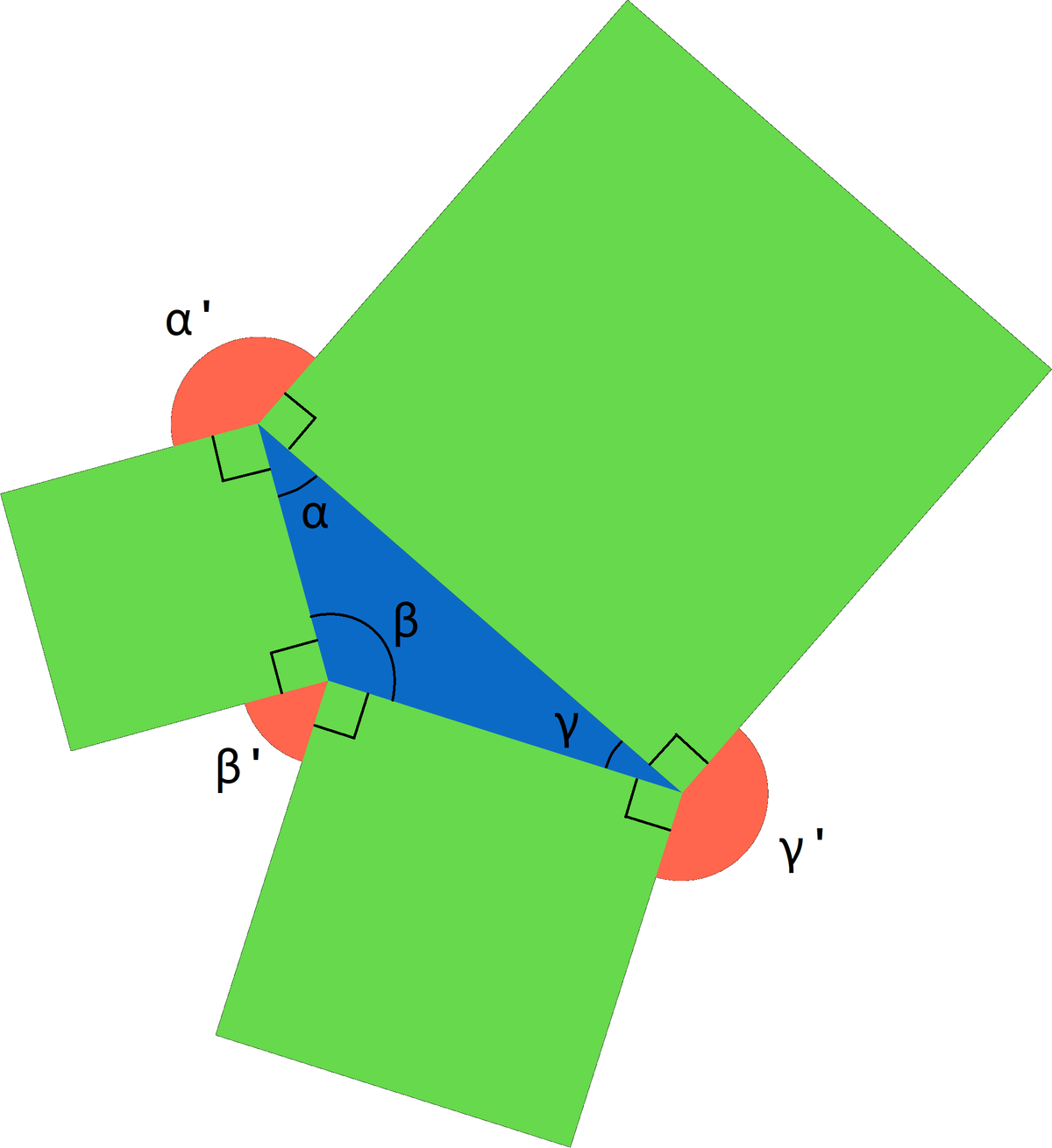
We know, that sum of the angles in every triangle is 180°. We can write it as:
α + β + γ = 1 8 0 °
We also have a red angles here. Since there are two more 90° angles in every vertex of the triangle, we can express other three angles as follows:
α ′ = 1 8 0 − α
β ′ = 1 8 0 − β
γ ′ = 1 8 0 − γ
Let's make a sum of these three red angles now:
α ′ + β ′ + γ ′ = ( 1 8 0 − α ) + ( 1 8 0 − β ) + ( 1 8 0 − γ ) = 5 4 0 − α − β − γ = 5 4 0 − ( α + β + γ ) = 5 4 0 − 1 8 0 = 3 6 0 °
So, we can say:
The sum of the three red angles will always equal 360° regardless of the type of triangle drawn.
And now, let's solve the bonus question.
The sum of three 360° angles in three vertices is:
3 6 0 + 3 6 0 + 3 6 0 = 1 0 8 0 °
Since we already know the sum of all red angles, which is 360°, we can calculate:
1 0 8 0 − 3 6 0 = 7 2 0 °
There is a solution (a set of yellow angles):
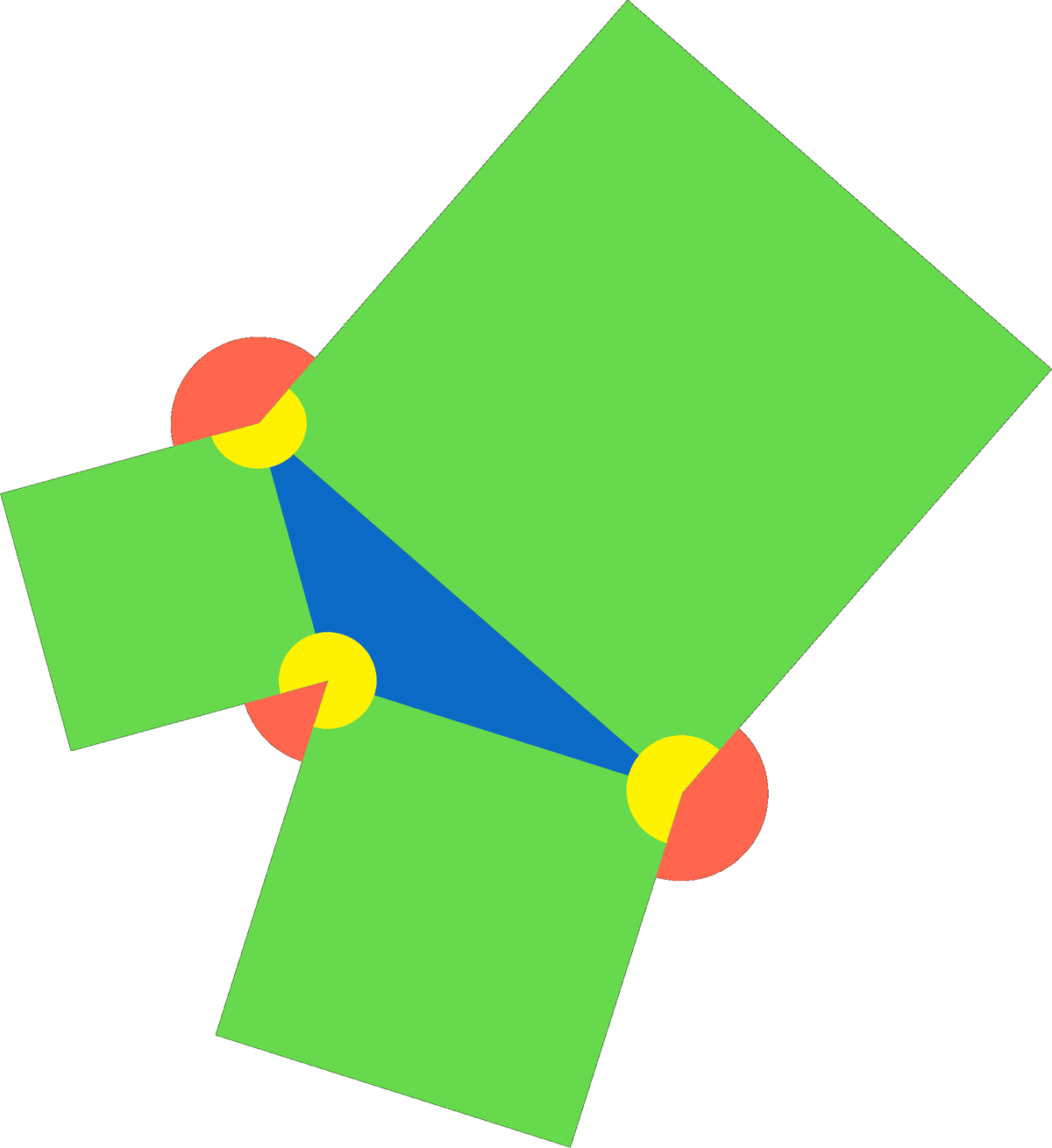
Just take it to the limit as the smallest angle approaches 0 the other 2 approach 180
Let's start assuming that the internal angles of the triangle are α1, α2 and α3. As we know, the sum of all internal angles in a triangle must equal to 180º. So, α1 + α2 + α3 = 180º
Let's call the angles opposed to the internal angles of the tringle β1, β2 and β3, in such a way that the angle opposed to α1 is β1, and so on. Therefore, what the problem is asking is if there is true that β1 + β2 + β3 = 360º
Now, we can close a circle with the α and β angles, i.e. the internal angles of the triangles and the ones opposed to them, but to do that, we need to cover two square angles from the squares, i.e. 2x 90º.
Matemacally saying, that means:
α1 + β1 + 90 + 90 = 360 ; α2 + β2 + 90 + 90 = 360 ; α3 + β3 + 90 + 90 = 360;
Or,
α1 + α2 + α3 + 90 + 90 + 90 + 90 + 90 + 90 + β1 + β2 + β3 = 360 + 360 +360
Cutting the sum of alpha angles + 2x90 with 360, we get:
β1 + β2 + β3 + 90 + 90 + 90 + 90 = 360 + 360
Since 4x90 = 360, we get:
β1 + β2 + β3 = 360
So, it is true.