88 of 100: The Second Rule of Octagon Club Is Don't Talk About Octagon Club
Above is a simple octagon (that is, one where the sides don't intersect) where 4 of the internal angles (marked in blue) are acute.
Given any simple octagon, what's the maximum possible number of acute internal angles?
It's possible to get a good idea of the solution by just drawing some octagons, but the best solution will also prove you can't do better!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Another interesting argument for an upper bound is as follows. If we have 7/8 acute angles, we must have 7 consecutive acute angles, and this is simply not possible without the shape intersecting itself. Thus there must be less than 7 and you again show that there is a 6 configuration that works.
Log in to reply
"If we have 7/8 acute angles, we must have 7 consecutive acute angles, and this is simply not possible without the shape intersecting itself. "
It's certainly possible to draw 7 consecutive acute angles without the shape intersecting itself. (The last angle is where the difficulty arises.)) You need to say more here. The fact that it's impossible to draw the last side is equivalent to the statement you're trying to prove. This feels like a circular argument.
Log in to reply
You are correct of course, the statements are equivalent but I thought this fact was fairly intuitive, as we can see that the shape must spiral in on itself and together we can have at most two connected spirals, each with only three vertices, for if we add a fourth, the last points cannot connect to each other. We can make this formal since the exterior angles must add up to more than 360+180=540 degrees so we cannot have a line connecting the two ends. Also sorry for the confusion about drawing in the last angle, I consider shapes to be closed so it was implied that the last points would have to connect to each other/
Excellent solution - I merely worked out that the internal angles of an octagon add to 1080 degrees, and that the most seven acute angles could add up is just less than 630, leaving over 360 degrees for the remaining angle, which of course is not possible. I then worked out that six acute angles could add up to just less than 540 degrees, leaving two reflex angles to add up to just over 540 degrees. Your example drawing of on octagon with six acute angles confirms that it is possible.
A systematic way to develop a working example with 6 acute angles is to start by building with right angles.
- Start with a base, A.
- Add two equal perpendicular sides, B and C, rising up from the two ends of the base.
- Add two more equal sides, D and E, moving inward from the tops of B and C, and perpendicular to them, leaving a gap between D and E.
- Then two more sides, F and G, moving perpendicularly downward from the inner endpoints of D and E, stopping above base A.
- Finally, join the remaining endpoints of F and G with a new side, H.
You now have six right angles, and two 270-degree angles at the ends of H. By reducing each of the right angles slightly - and enlarging the 270-degree angles slightly - you will have constructed an octagon meeting the requirements of the problem.
Log in to reply
This is how I did it, though my shape is different. You have a 'u' shaped figure while mine is an 's'.
For anybody who wants to see this in the Cartesian plane, use points at (0,1), (1,1), (1,0), (2,0), (2,2), (1,2), (1,3), (0,3), and back to (0,1).
For Tetris players, this shape will be familiar.
It's easier to see that small distortions to each corner can produce a figure with 6 acute angles.
We know, for a 'n' sided polygon the sum of all internal angles=2×(n–2)π/2.
So for an octagon this.
sum=2×(8–2)π/2.
=6π.
Now if, 8 angles are acute, then the sum will be<{8×π/2}=4π.
So, it can not be true.
If 7 angles are acute then the sum of those 7 angles is<{7×π/2}=3.5π.
Then, the rest angle must be greater than (6π–3.5π)=2.5π which can't exist.
If 6 angles are acute, then the sum of those 6 angles is<{6×π/2}=3π and the sum of other 2 angles>(6π--3π)=3π.
So it can exist.
Hence the answer is 6
Great solution.
Bound provided but no example showing bound can be achieved.
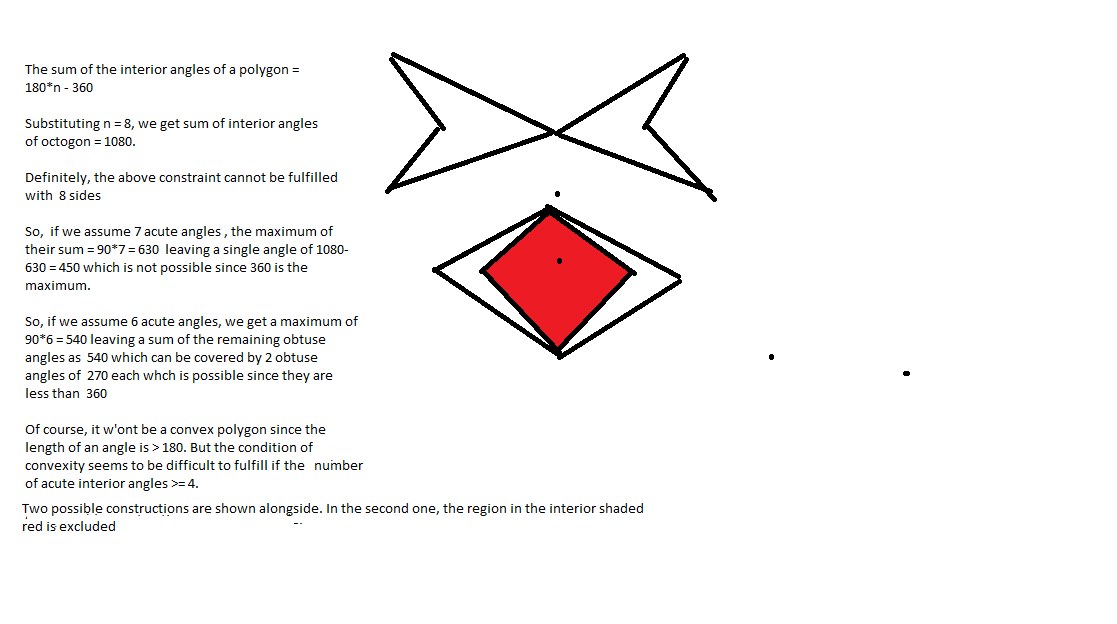
Let the internal angles be α i . Then ∑ i = 1 8 1 8 0 − α i = 3 6 0 . Hence, ∑ α i = 8 × 1 8 0 − 3 6 0 = 6 × 1 8 0 = 1 2 × 9 0 . We also know α i < 3 6 0 .
If k angles are less than 9 0 , then this must be 'compensated' by the other 8 − k angles. Thus, we get 1 2 × 9 0 = ∑ α i < k 9 0 + ( 8 − k ) 3 6 0 = ( 3 2 − 3 k ) 9 0 . Hence, 1 2 < 3 2 − 3 k , or k < 2 0 / 3 < 7 .
Maximum k = $ 6 $ . Six angles just under 90, can be compensated by two angles just over 270.
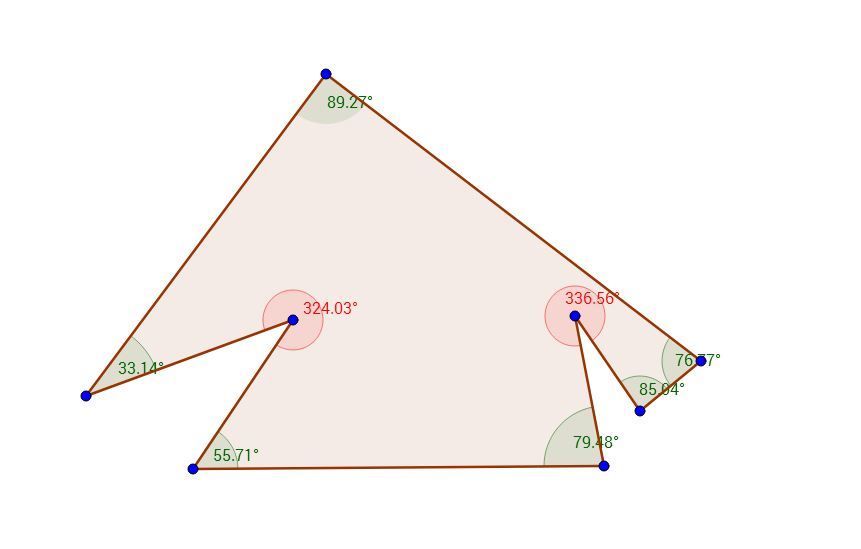
For this maximum number, the acute angles can even be just over 60 (see picture): 6 × 6 0 + 2 × 3 6 0 = 6 × 1 8 0 .
Your diagram shows the extreme case very well. Regards, David
You are supposed to find for simple octagons. Your figures seem to contradict that.
I presume , by simple you mean "convex". Basically once you have at least 1 angle greater than 180, you sacrifice convexity as evidenced by the cusps which are present even in the example. Or do you mean simply connected ? Then, possibly the second figure should not be included
By simple it means that sides do not intersect. It is mentioned in the question. Convex has nothing to do with it supposedly.
Total angles = 4(180) + 360 = 1 0 8 0 o
The figure has at least 4 acute angles, so
Sum of remaining angles > 1080 - 4(90) = 7 2 0 o
If it has another acute angle, then
Sum of remains angles > 720 - 90 = 6 3 0 o
And if it has another acute angle, then
Sum of remaining angles > 630 - 90 = 5 4 0 o
And if it has another acute angle, then,
Sum of remaining angles > 540 - 90 = (450^{o}_
So this shows that it can not have another acute angle because the last angle,
will be greater than 360 degrees. So if it has 6 acute angles, Here is a picture what it looks like:

Not sure that your arrowhead is octagonal.
Log in to reply
At least the critical six angle octogon was. Left off the obtuse bump in the middle copying my drawing to MS Paint. Fixed it and made a better 6 acute angle octagon also.
The fletching of the arrowhead contains six sides - two long diagonals with four shorter diagonals forming the shorter indent, these six sides can be thought of as collectively forming one side of a deformed triangle, and the two longer sides remain for a total of eight = octagon.
Log in to reply
Thanks Thomas. You know Robert edited the drawing, right? I can count to 7, sometimes even 8 if I have to.
The easiest and most basic strategy is to do eenie meenie miny moe. Guaranteed 100% success rate.
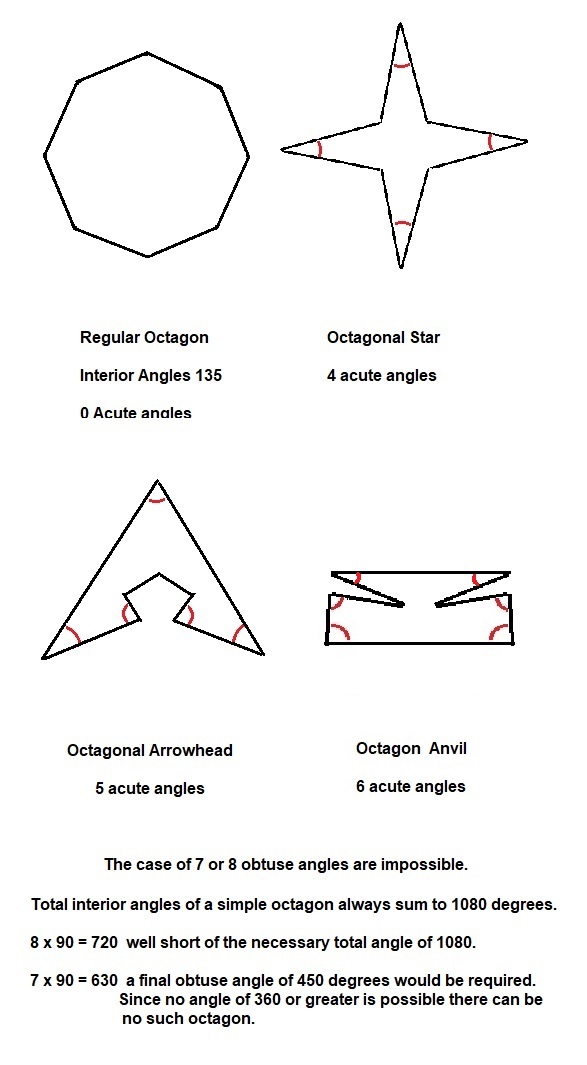
Let's find an upper bound by going to the extreme. Assume that n internal angles are 9 0 ∘ and 8 − n angles are 3 6 0 ∘ . So,
n × 9 0 ∘ + ( 8 − n ) × 3 6 0 ∘ = ( 8 − 2 ) × 1 8 0 ∘ ⟹ n × 9 0 ∘ + ( 3 2 − 4 n ) × 9 0 ∘ = 1 2 × 9 0 ∘ ⟹ 3 2 − 3 n = 1 2 ⟹ n = 3 2 0
What we really need is n angles each less than 9 0 ∘ . So, there's no way of attaining the upper bound we just found. Hence, we'll be taking the floor function of n . Or in other words, we'll take the largest integer less than n .
⌊ n ⌋ = ⌊ 3 2 0 ⌋ = 6
Now, it's only left to show that 6 acute internal angles are indeed attainable!