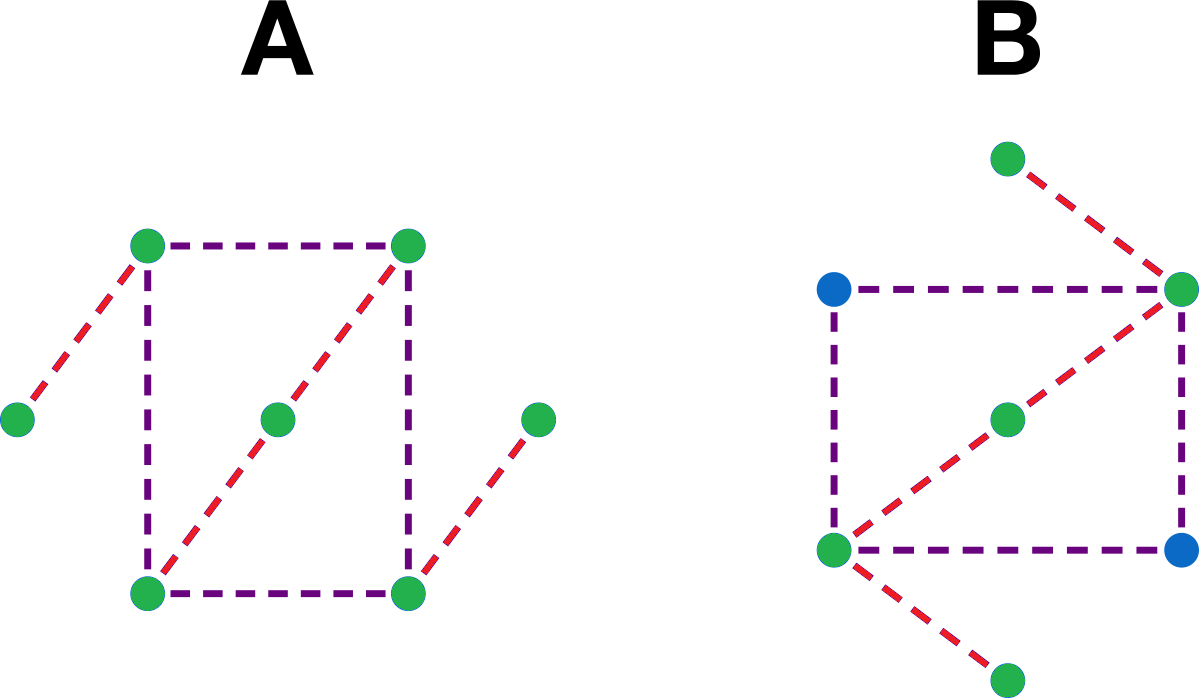
93 of 100: Connect the Dots
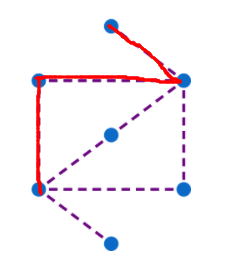
For which of these pictures is it possible to trace a path along the dashed lines (not necessarily all of them) that visits each dot exactly once ?
Remember, while each dot must be visited exactly once, your paths do not have to include every dashed line.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Can you show that there is no way to color the vertices aside from 5 red and 2 blue (or 5 blue and 2 red) please? That is the only part of your proof that is not clear to me.
Log in to reply
Since all vertices will be colored regardless of where we start, we can pick where to start coloring. Blue and red are arbitrary anyways. So, without loss of generality, assume that the bottom-most vertex is red. Working up from the bottom and ensuring that no two adjacent vertices are the same color, you get that the only two blue vertices in the graph are the endpoints of the diagonal. If you start with any vertex, then there is exactly one way to color the graph. Therefore, the color of the bottom vertex is fixed regardless of where you start, allowing you to make this assumption and start there. (I don't really think I answered your question still). Basically parity (evens vs odds) argument shows that there will be 5 of one kind and 2 of the other.
Log in to reply
Thanks! I think I understand it now—in fact, having thought about it, it seems the fact that there is only one coloring scheme should have been intuitively obvious to me from the start. Perhaps a way to achieve this intuition is to color in the graph from an arbitrary point and then, without removing the colors, imagine that you started coloring at a different point. Could you have possibly gotten different colors if you had colored in from that different point instead of the original arbitrary point?
To solve this, we must make 3 vital observations.
-
You cannot revisit a path.
-
Certain paths MUST be taken or else it may be impossible to solve. (Highlighted red)
-
After leaving a 'compulsory path', we are unable to use that path again in the same direction.
1 is easy to prove. After visiting a path, if we revisit it, we would be stuck as we could not go forward or backward, due to the restriction that we must visit each dot once.
To prove 2, we use observation 1.
In A and B, the center path and the paths going away from the rectangle are 'compulsory paths'.
This is because the center path contains a dot, and after visiting the dot, we must exit out the only other way, as we are unable to reuse paths.
The paths extending away are obvious, as there is only one way to get to the dots on that path, so they must be the starting and ending points.
Finally, 3. We can prove this by logic, and observations 1 and 2.
Let's say we have a triangular path ABC. AB is a compulsory path. By Travelling A > B, we are done. If we try to go A > C first, we must go C > B. Although we have gone from A > B, we have failed to use the compulsory path AB. We left the path AB, and are unable to rejoin as we are not allowed to revisit A.
Thus, we can make a conclusion that if we are on the starting point of a compulsory path, we cannot leave the path. Or else, we will not be able to pass by what is inside that path. This is important, as the center paths contain a dot that cannot be missed.
In A, all points are on a compulsory path.(Highlighted green) Thus, by using the 'optional paths' to connect the 'compulsory paths', we are able to solve the question.
However, in B, only 5 are on compulsory paths, and the compulsory paths are all connected.
From 3, we know that if we were to leave the path, it would be impossible to get all points.
But at the same time, if we were to follow the compulsory paths, we would miss 2 points on the side.
A i s p o s s i b l e B i s n o t
(A) can be done easily.
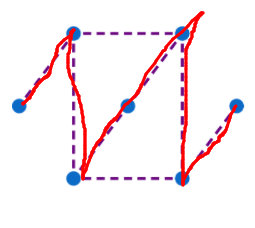
However, (B) is impossible. Three different failing paths are shown.
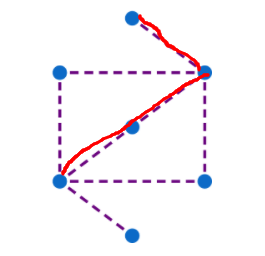
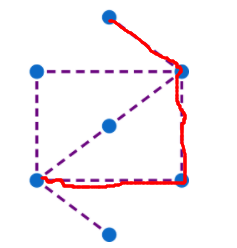
Is anyone else annoyed about the wording? The original question does not include the phrase "not necessarily all of them" which completely changes the nature of the problem!
Log in to reply
It didn't change the nature of the question, it just made it more clear. The question never said you had to use all of them.
In Picture A , you can use the diagonal to cut through to the other parallel line and thus visit each dot exactly once. It is vital to observe that first you move down and then you move to the parallel line, unlike in Picture B .
In Picture B , you take the the diagonal cut to the other parallel line immediately and hence you cannot visit each dot only once, you have to atleast visit two dots twice.
Therefore, the answer is Only A .
Ah... that’s why I fail in exams... misreading the question! I thought, GIVEN the paths, how to trace each line on the paths once, whereas it was about the dotted paths being POSSIBILITIES and which of the two allows you to VISIT each dot exactly once... Well, there we have it: most mistakes are interpretation mistakes, which are stupid and could, in fact, be easily avoided by CAREFULLY reading the question!
Not sure if I misunderstand your comment on Picture A, but you can actually move in two directions from the top left corner and successfully touch each dot. Assuming a start position of the left-most dot, after the initial move to top left corner, you can go right > down diagonal left > right to reach bottom right corner (similar to a Z shape) or down > up diagonal right > down to reach the bottom right corner (similar to a backward N). But nevertheless, you are correct that only Picture A is possible to touch each dot once.
Log in to reply
Yes, you are right, you can move down or move right. I just mentioned one as an example. But thanks for pointing it out!
For A a path is easy to find.
For B it is evident that any such path must start and end on the dangling leaf verfices. Start at the top. From the upper-right corner, if you proceed across the diagonal, then from the lower right you cannot reach all three other vertices without getting stuck. If you proceed to a corner (UL or LR), the only next choice is to LL, and again there are 3 unvisited nodes remaining, any one of which leaves you stuck.
So B is not possible.
A can be traversed quite simply. Let us examine B. Any graph covering path has to begin and end at the top or bottom vertices, i.e starting at the top vertex and ending at the bottom vertex or vice versa, These paths would pass through the two vertices at the opposite corners of the closed figure. But these vertices are also the only neighbors for 3 other vertices which would mean that these vertices would have to be visited more than once in any traversal of the graph.
Since the eulerian path problem (traversing edges without revisiting) is possibly simpler, one could possibly convert the above graph to its dual , (i,e convert edges to vertices and vice-versa)
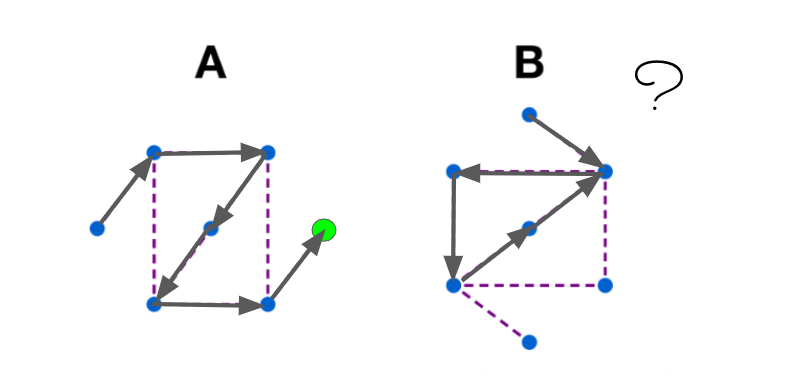
The path for A is pretty obvious.
Most of the solutions I see so far prove that B is impossible by exhausting possibilities, rather than exploring graph theory, so here is my solution without exhausting possibilities.
Start with any vertex on part B, color it red. Color all adjacent vertices to that red vertex blue. Repeat until the graph is colored such that no two connected vertices share the same color.
The graph should end up with 5 red vertices and 2 blue (or 5 blue and 2 red depending on which vertex you picked first).
Every time you leave a vertex, you must go to a vertex of a different color, because that's how we colored the graph. So our path should visit vertices in alternating colors such as RBRBRBR or BRBRBRB. However, this is impossible due to the colors of our vertices being not 3 of one color and 4 of the other. Thus, graph B does not contain a Hamiltonian Path
You can color graph A as well to check, and it turns out there are 3 of one color and 4 of another color, thus allowing such an alternating color path.