94 of 100: Cross Sections
How many of the following 8 shapes can be created by taking a cross section of a cube?
| Equilateral Triangle | Scalene Triangle |
| Isosceles Triangle that is not equilateral | Square |
| Rectangle that is not a square | Pentagon |
| Hexagon | Octagon |
A cross section is the resulting shape that's on the surface of the plane when a plane slices through a figure. Examples using a cylinder are shown below.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Your drawings really help. To me, the pentagon drawing doesn't appear to be flat (a plane). I may be wrong. Arjen's explanation has one point at a vertex, which I can see will work.
Nice drawings.
Very well illustrated.
very neatly illustrated and explained
The cross-section is a polygon, and each side of that polygon is the result of intersecting a face of the cube. Since there are only six cube faces, the cross-section can have no more than six sides. This rules out the octagon . The seven other shapes mentioned here are possible:
Let the vertices of the cube have coordinates ( ± 1 , ± 1 , ± 1 ) . Consider the plane x + y + z = 3 − ϵ , where ϵ < 1 is a positive number. This plane intersects the cube in the points ( 1 , 1 , 1 − ϵ ) and permutations thereof; symmetry shows that this is an equilateral triangle .
Now tilt the plane a bit, e.g. x + y + 3 4 z = 3 − ϵ . The intersections are ( 1 , 1 , 4 3 − 4 3 ϵ ) , ( 1 − ϵ , 1 , 4 3 ) and ( 1 , 1 − ϵ , 4 3 ) . This is symmetric under reflection around x = y , so that the triangle is isosceles . It is not hard to see that it is not equilateral.
A further twist gives e.g. x + 4 5 y + 3 4 z = 3 − ϵ , destroying all symmetry. Now we have a scalene triangle.
Move the plane closer to the center: x + y + z = ϵ , where ϵ < 1 is positive. Intersections are ( ∓ 1 , ± 1 , ϵ ) and all permutations thereof, for a total of six intersection points. This is a hexagon .
Now consider the extreme case x + y + z = 1 . The intersection is now a large equilateral triangle, whose vertices are all permutations of ( 1 , 1 , − 1 ) . Now tilt the plane, keeping one of the intersection points in place; e.g. x + y + 5 6 z = 5 4 . The intersection points ( 1 , 1 , − 1 ) ; ( 1 , − 1 , 3 2 ) ; ( 5 3 , − 1 , 1 ) ; ( − 1 , 5 3 , 1 ) ; ( − 1 , 1 , 3 2 ) form a pentagon .
The square is easy: take e.g. the plane x = 0 , and the intersection has points ( 0 , ± 1 , ± 1 ) .
For the rectangle , intersect with x + 5 y = 0 , and get the intersection points ( ∓ 5 1 , ± 1 , ± 1 ) , where the signs of x and y are opposites.
Note : It is not possible to make any kind of polygon with six sides of less. For instance, polygons with 4, 5, 6 sides will have one, two, or three pairs of parallel sides, respectively.
I like how you use coordinate geometry to tackle this problem.
Log in to reply
I was too lazy to draw the diagrams :D
Y Wu did a great job of that.
One day I will be this smart!!
Your note at the bottom brings up an interesting follow up question... i.e. Can all triangles be made? Or all acute triangles?
Log in to reply
It appears that all acute and right triangles can be made up to similarity.
Proof that you cannot make an octagon:
Assume there is a cross section that creates an octagon. There are 8 edges on an octagon. Spread among 6 faces, at least 1 face will have 2 edges of the octagon (by the Pigeonhole Principle ). However, it is impossible to have a plane intersect a single face in more than one line, by simple 3D geometry. Thus any shape with >6 edges cannot be created.
Showing that up to hexagon can be created is an exercise left to the reader :)
An octagon is not possible because an octagon has 8 sides and every side has to be in a face of the cube, but a cube has only 6 faces.
The other 7 shapes are possible.
- Equilateral Triangle
- Isosceles Triangle that is not equilateral
- Rectangle that is not a square
- Hexagon
- Scalene Triangle
- Square
- Pentagon

All of the possible shapes are possible except for Octagon. Here are the pictures to prove it:
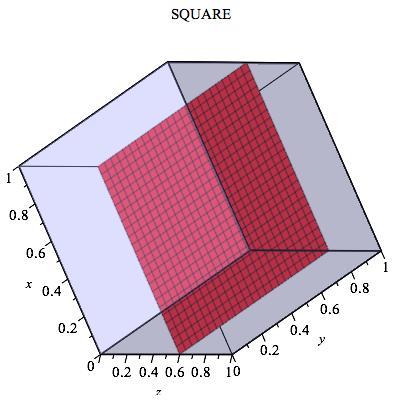
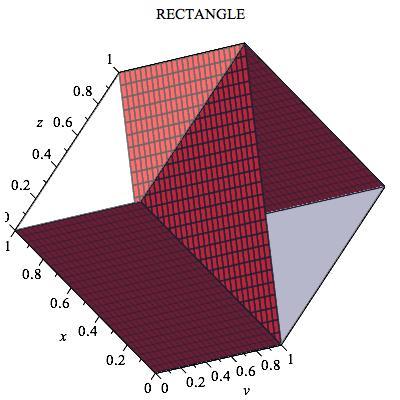
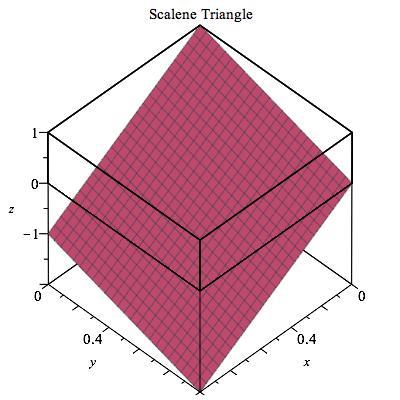
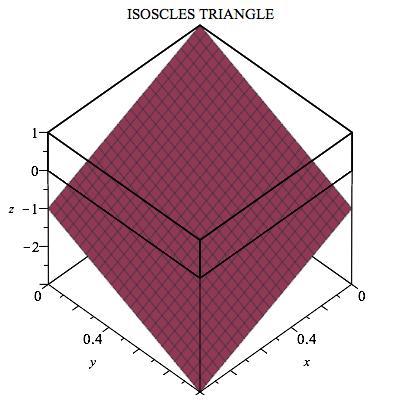
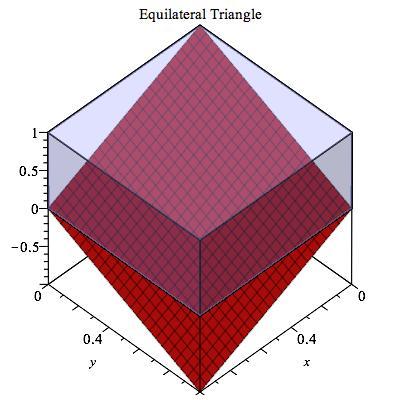
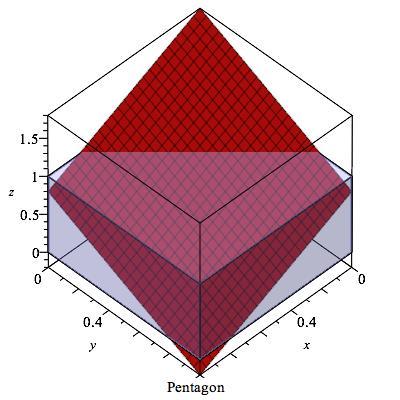
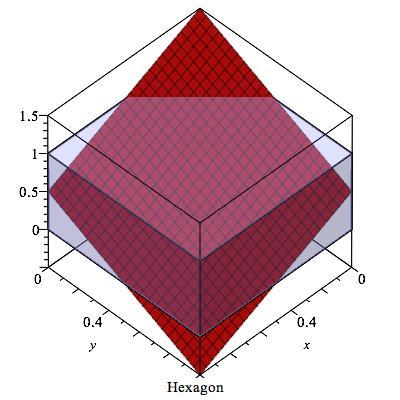
Interestingly, the answer would be 8 in a 4-d cube and more generally 2*n in n-d cube.
I think it is impossible to make octagon
But it is easy to make other shapes
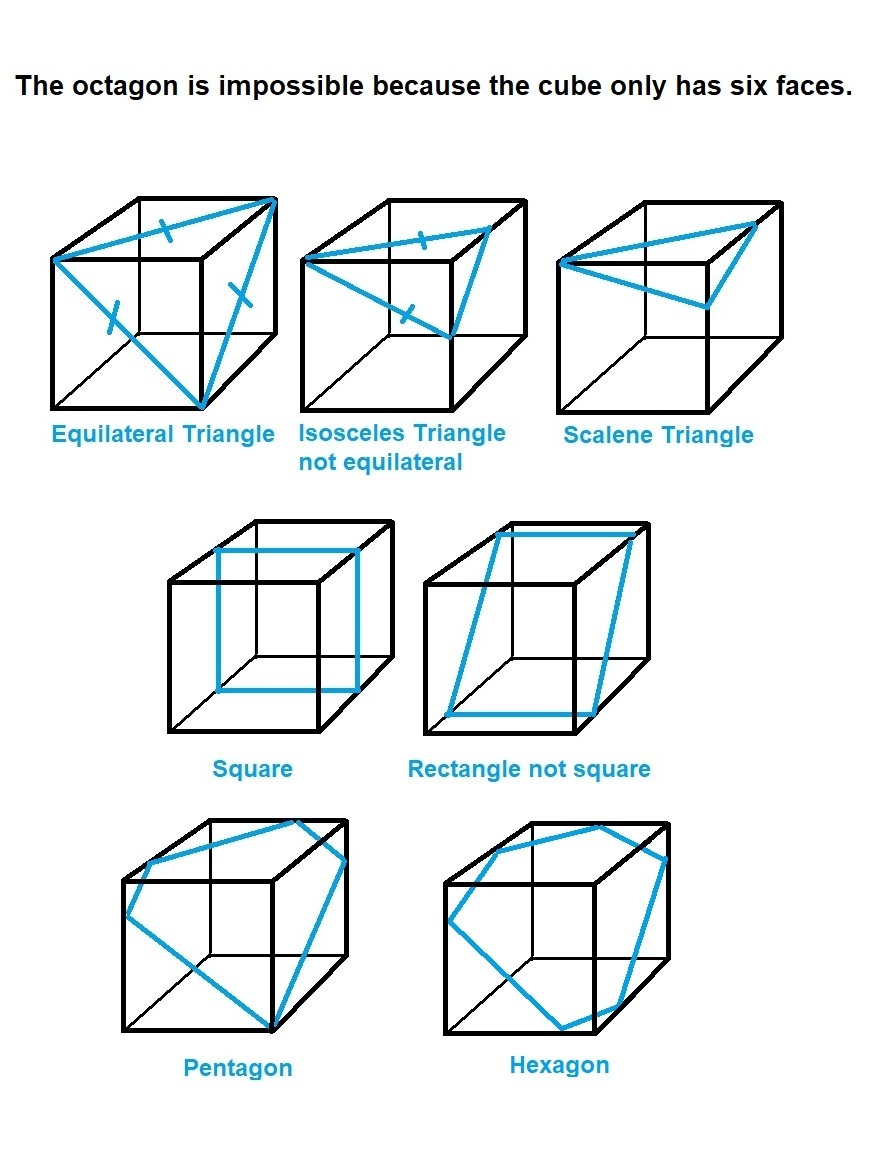
It is possible to create all of the listed shapes by taking a cross-section of the cube except an octagon.
Equilateral triangle: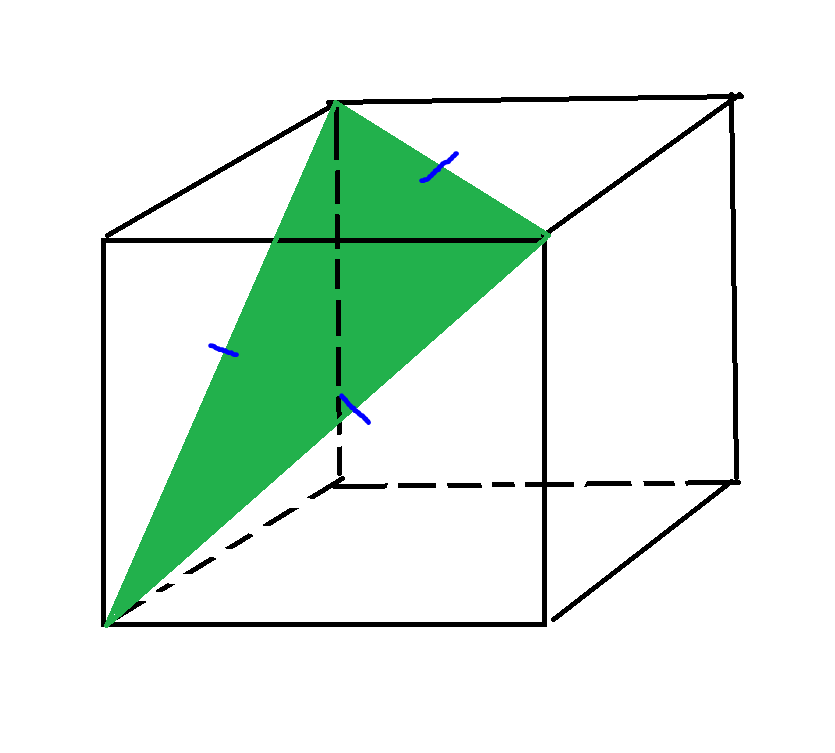 Isosceles Triangle that is not equilateral:
Isosceles Triangle that is not equilateral:
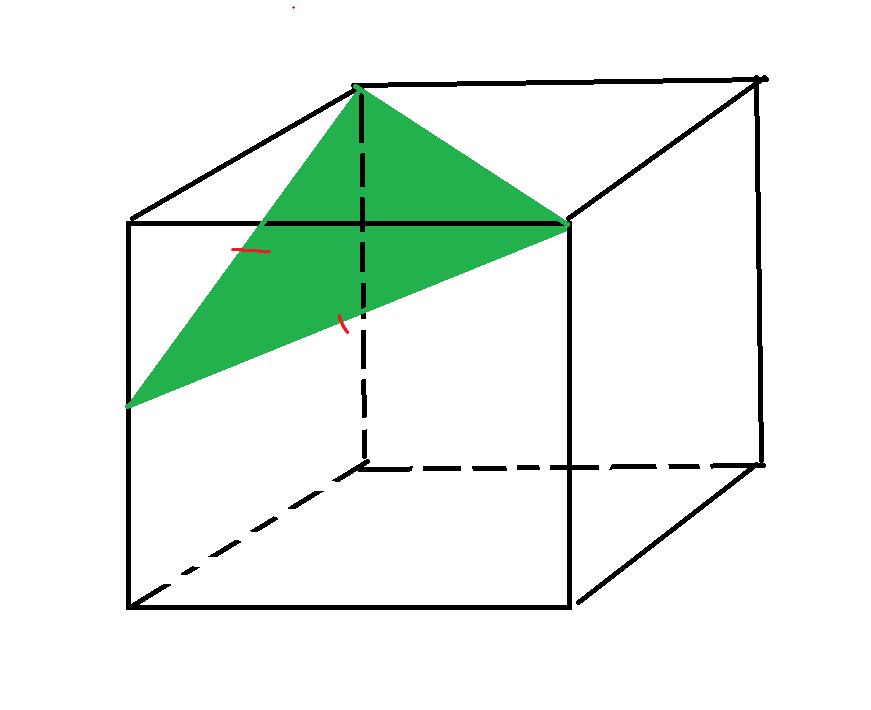 Scalene Triangle:
Scalene Triangle:
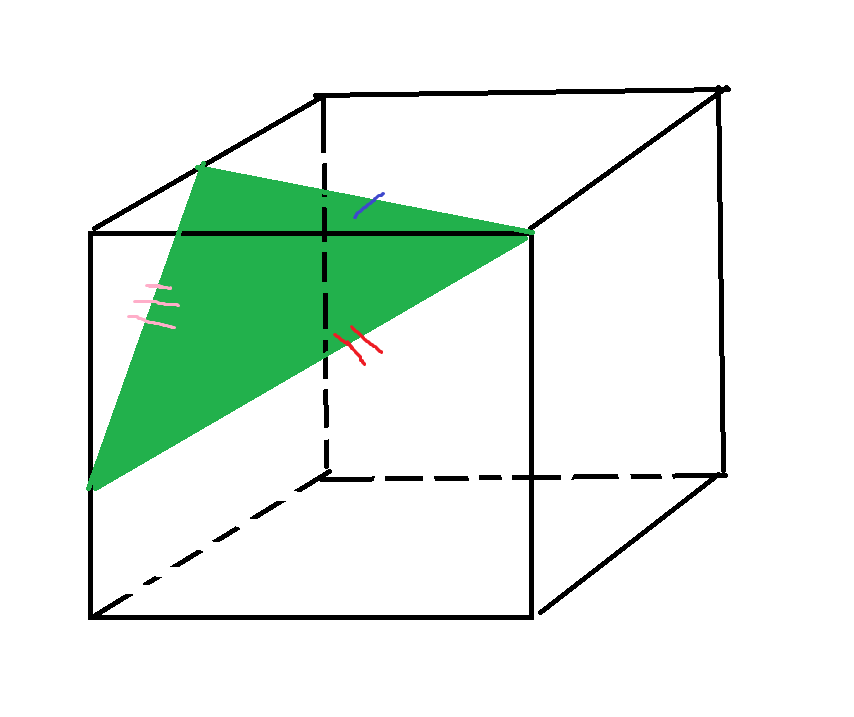 Rectangle that is not a square:
Rectangle that is not a square:
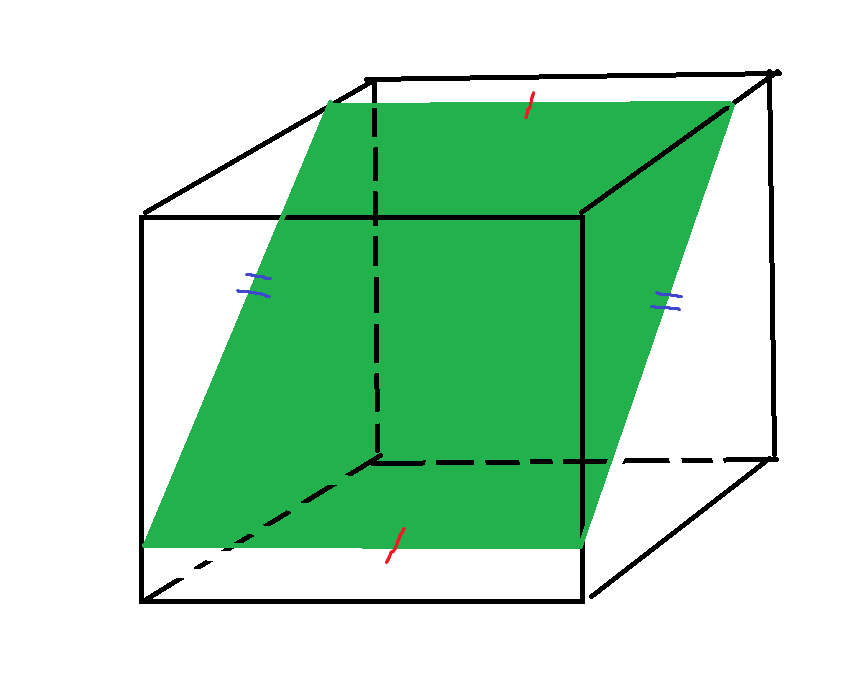 Square:
Square:
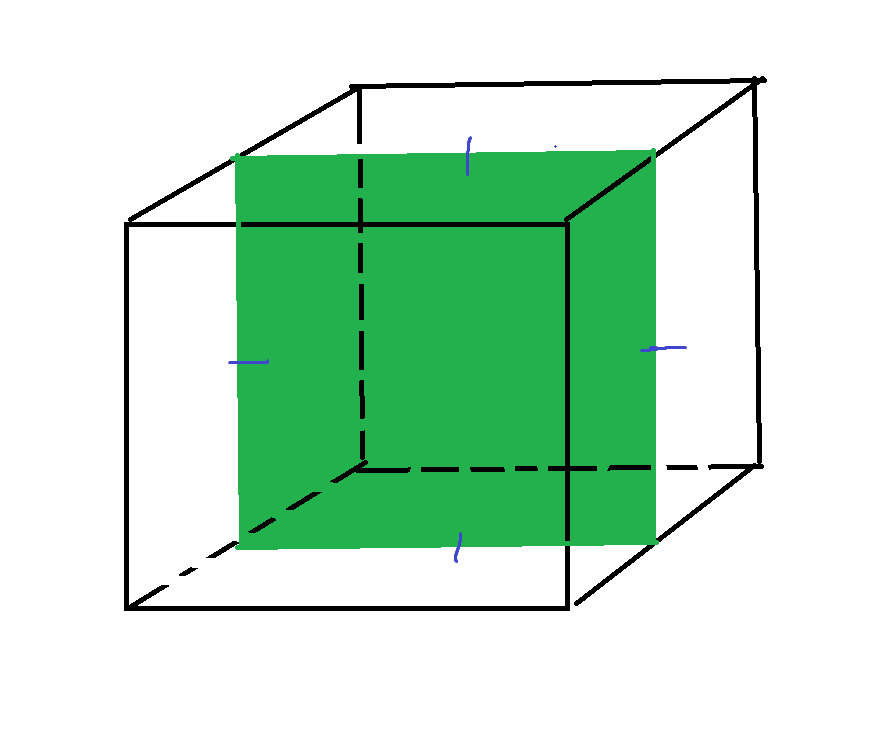 Pentagon:
Pentagon:
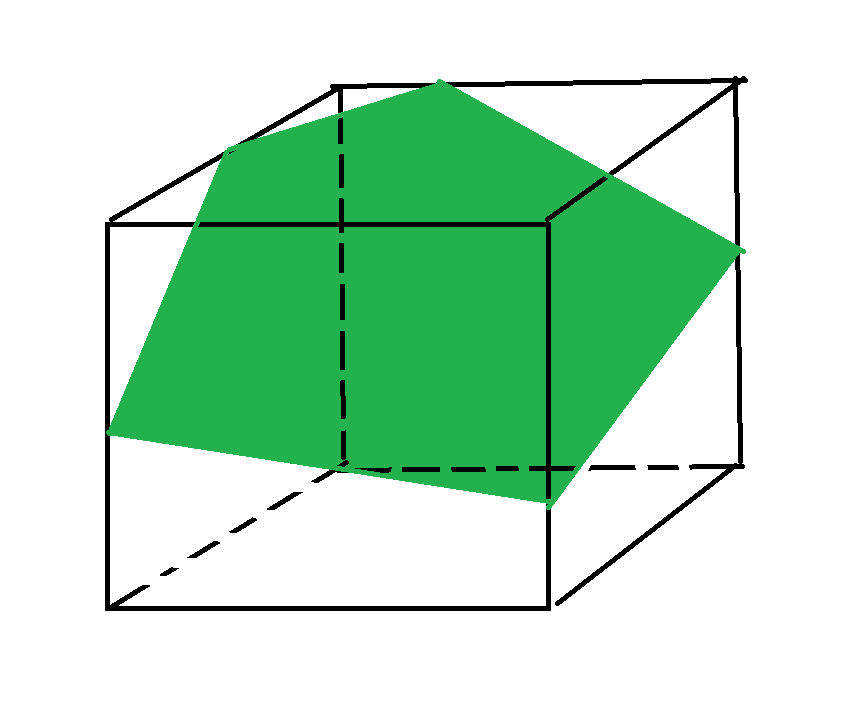 Hexagon:
Hexagon:
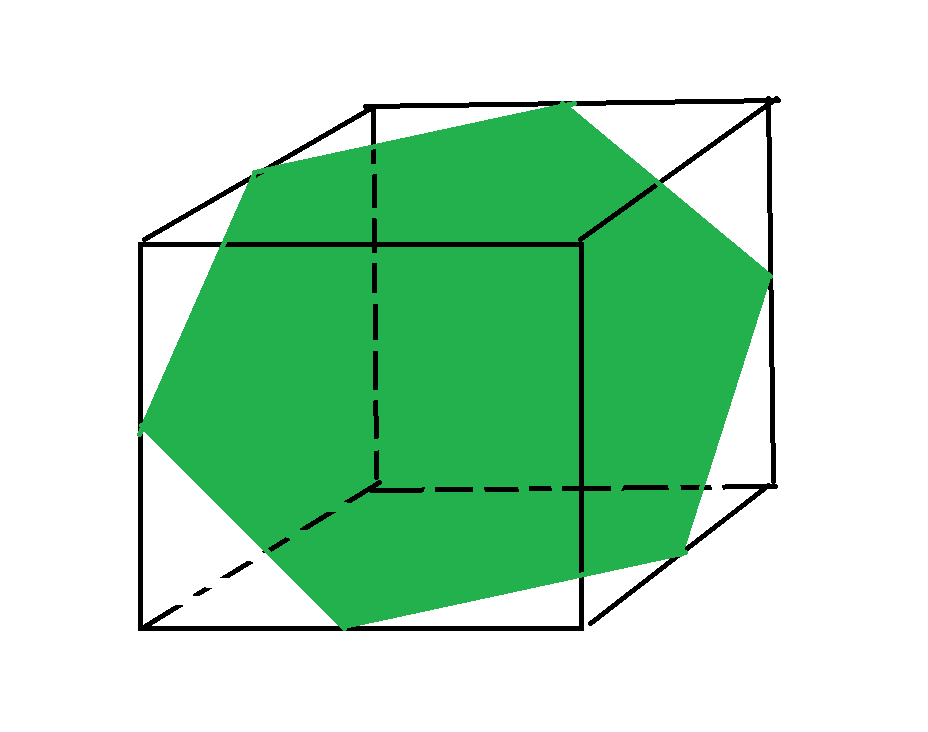
However, since 3 points make a plane, we cannot have more than 2 points on each face of the cube, therefore we can only have a maximum of 6 points on the cube (which makes a hexagon). Thus, it is impossible to create an octagon by taking a cross-section of a cube and the answer is 7 .