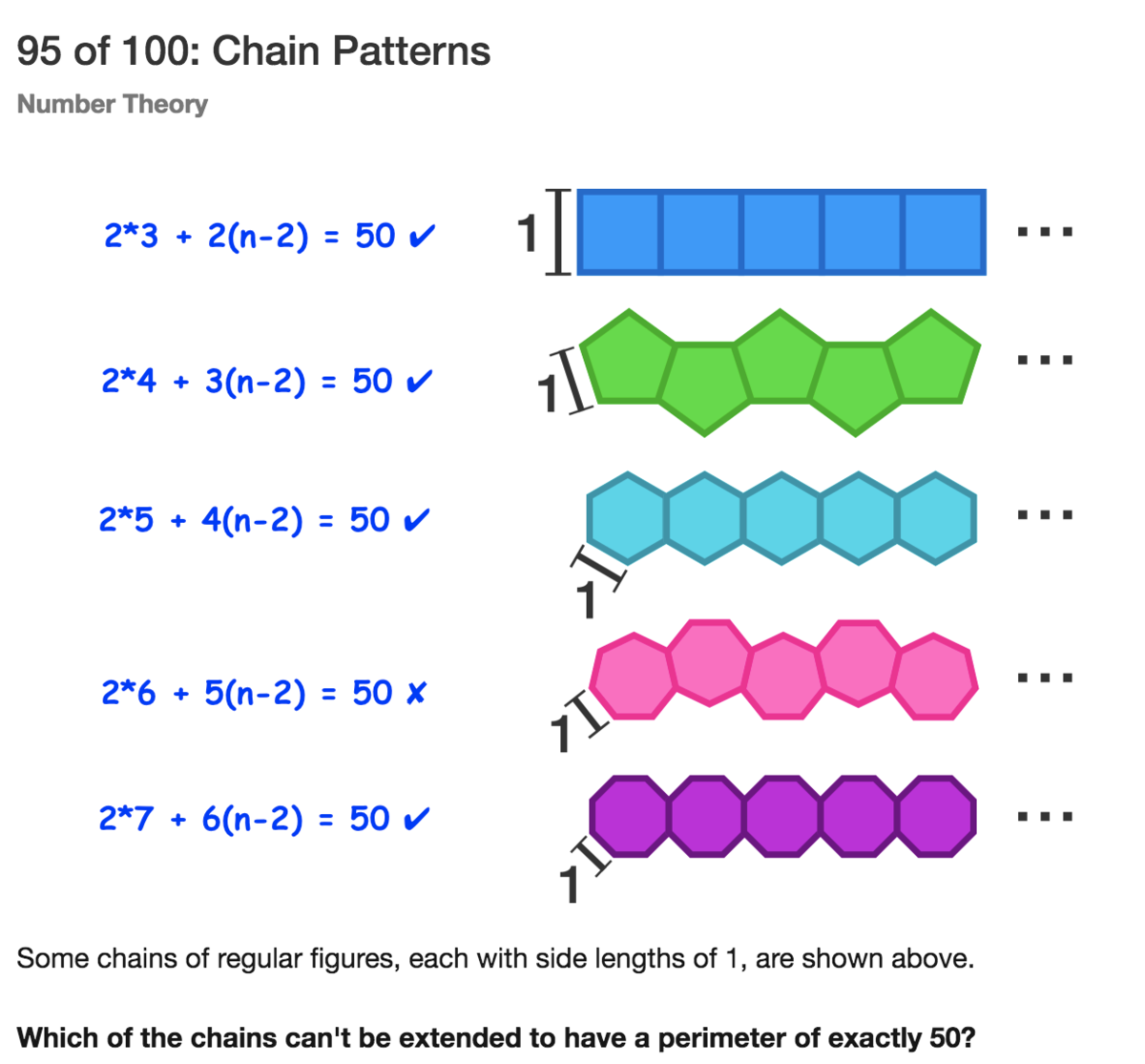
95 of 100: Chain Patterns

Let's find all chains that have the desired property.

Observe that if the number of $n$ -polygons in the chain is $k$ , then the resulting extended perimeter will be $kn-(k-1)\times 2=k(n-2)+2$ .

We need $k(n-2)+2=50$ or $k(n-2)=48$ . Thus $k=\frac{48}{n-2}$ and $n-2$ must be a divisor of $48$ . Divisors of $48$ are $1, 2, 3, 4, 6, 8, 12, 16, 24, 48$ .

Thus $n$ can be ${\color{#D61F06}3}, {\color{#D61F06}4}, {\color{#D61F06}5}, {\color{#D61F06}6}, {\color{#D61F06}8}, {\color{#D61F06}10}, {\color{#D61F06}14}, {\color{#D61F06}18}, {\color{#D61F06}26}, {\color{#D61F06}50}$ . As it can be seen $n=7$ is not a solution to the equation $k(n-2)=48$ since it doesn't provide an integer value for $k$ .

So the answer is heptagon.

---

As an example, for $n=3$ , we obtain $k=48$ and this chain of equilateral triangles makes an $1 \times 24$ parallelogram with a perimeter of $50$ .

Square Chain - The first and last square extend its perimeter by 3 while all the squares in between extend the perimeter by 2 : 50 - 3 - 3 = 44 which is divisible by 2, so it can be extended to 50.

Pentagon Chain - The first and last pentagon extend its perimeter by 4 while all the pentagons in between extend the perimeter by 3 : 50 - 4 - 4 = 42 which is divisible by 3, so it can be extended to 50.

Hexagon Chain - The first and last hexagon extend its perimeter by 5 while all the hexagons in between extend the perimeter by 4 : 50 - 5 - 5 = 40 which is divisible by 4, so it can be extended to 50.

Heptagon Chain - The first and last heptagon extend its perimeter by 6 while all the heptagons in between extend the perimeter by 5 : 50 - 6 - 6 = 38 which is NOT divisible by 5, so it CAN NOT be extended to 50.

Octagon Chain - The first and last octagon extend its perimeter by 7 while all the octagons in between extend the perimeter by 6 : 50 - 7 - 7 = 36 which is divisible by 6, so it can be extended to 50.

Therefore, the Heptagon Chain is the only chain that can NOT have a perimeter of 50.

Observe that the perimeter of every chain of a regular polygon with number of sides $n$ can be generalized as follows: one leftmost side from the first polygon, $n - 2$ sides for every $k^{\text{th}}$ polygon in the chain, and one rightmost side from the last polygon. The expression $n - 2$ comes from the fact that every polygon in the chain has two sides connecting it to its adjacent polygons which are not part of the chain's perimeter $-$ that is, except for the first and last polygons, who have an extra non-connecting side. Thus, we can generalize their perimeters as

$P_n = k(n - 2) + 2$

For squares, we have

$P_4 = k(4 - 2) + 2 = 2k + 2 \left. \right|_{k = 24} = 50$

For pentagons, we have

$P_5 = k(5 - 2) + 2 = 3k + 2 \left. \right|_{k = 16} = 50$

For hexagons, we have

$P_6 = k(6 - 2) + 2 = 4k + 2 \left. \right|_{k = 12} = 50$

For heptagons, we have

$P_7 = k(7 - 2) + 2 = 5k + 2$

which cannot equal $50$ for some integer $k$ .

For octagons, we have

$P_8 = k(8 - 2) + 2 = 6k + 2 \left. \right|_{k = 8} = 50$

Thus, the $\boxed{\text{heptagon}}$ chain cannot have a perimeter of $50$ .

If the regular figure has $n$ sides, the first and last part of the chain contributes $n-1$ to the perimeter (because 1 side is connected to another part of the chain). All the parts in between contributes $n-2$ to the perimeter (because 2 sides are connected to other parts of the chain).

To let the perimeter of the chain be 50 subtract two times $n-1$ from 50. What's left over has to be divisible by $n-2$ . Or you can say: extending the chain to have a perimter of exactly 50 means $\frac {50-2 \times (n-1)}{n-2}$ has to be an integer.

For $n=4$ : $\frac {50-2 \times (4-1)}{4-2}=22$

For $n=5$ : $\frac {50-2 \times (5-1)}{5-2}=14$

For $n=6$ : $\frac {50-2 \times (6-1)}{6-2}=10$

For $n=7$ : $\frac {50-2 \times (7-1)}{7-2}=7\frac35$

For $n=8$ : $\frac {50-2 \times (8-1)}{8-2}=6$

Only if $n=7$ the answer is not an integer. So the heptagon-chain is not extendable to let it have a perimter of exactly 50.

In doing the arithmetic let n be the number of boxes needed to make up a figure with perimeter 50. One formula is 2*x + y(n-2) = 50 where x is the number of sides of the end polygons that contribute to the total perimeter and y is the number of sides that contribute to the total perimeter of the inside polygons. so if m is the number of sides of the polygon in question x = m-1 and y=m-2. So you can see that 50-2(m-1) must be divisible by (m-2). Or you could say that 2(m-1) must be divisible by (m-2).

Here is a picture:

The perimeter of a chain of congruent polygons can be found using the formula:

$2 + (number of tiles)(number of sides - 2)$

To derive this formula first, you have to consider that the perimeter is a result of how many tiles make up a chain. Since the polygons in between the first and last tiles all intersect with two sides of other polygons, those sides are neglected, hence we get the (number of tiles)(number of sides - 2) portion. The polygons at each end of the chain only intersect with one side of another polygon, so there is one extra non-intersecting side for each of the two polygons.

The number of tiles will be defined as $t$ , and the number of sides will be defined as $s$

$2 + t(s - 2)$

Since we are looking for a polygon that can't make a chain with a perimeter of 50, we'll have to set up the following equation:

$2 + t(s - 2) = 50$

$2 + t(s - 2) - 2 = 50 - 2$

$t(s - 2) = 48$

Next, we'll need to figure out if a certain number of tiles can be used in order to get a perimeter of 50, so we should solve for t, assuming that t is a whole number. If t is not a whole number, the value t is undefined.

$t = \frac{48}{s - 2}$

We can't get a perimeter of 50 with heptagons because $\frac{48}{7 - 2}\ = \frac{48}{5}$ , and 5 is not a factor of 48.

perimeter = numberOfShapesInChain*(numberOfSidesInShape-2)+2

1) 2 * 3 + 2X = 50 X = 22
2) 2 * 4 + 3X = 50 X = 14
3) 2 * 5 + 4X = 50 X = 10
4) 2 * 6 + 5X = 50 * X no answer in natural numbers X *
5) 2 * 7 + 6X = 50 X = 6

We can write the perimeter of each as an expression:

Shape = (number of sides - 1) sides at the beginning + (number of sides - 1) sides at the end + (number of sides - 2) every time we add a new shape.

Square = 3 + 3 + 2n

Pentagons = 4 + 4 + 3n

Hexagons = 5 + 5 + 4n

Heptagons = 6 + 6 + 5n

Octagons = 7 + 7 + 6n

Given the expressions, we can all equate them to the desired perimeter.

Square = 6 + 2n = 50
n = 22

Pentagons = 8 + 3n = 50
n = 14

Hexagons = 10 + 4n = 50
n = 10

Heptagons = 12 + 5n = 50
n = 7.6

Octagons = 14 + 6n = 50
n = 6

Since we cannot add fractions of a shape, the Heptagons chain will never have a perimeter of 50.

As each figure is connected with the next one, there are two sides that are not adding length to the perimeter of the total figure, but the first and last figure add two sides. As the perimeter of the total figure composed by a number $k$ of $n$ -sided regular polygons must be $50$ we have $50=2+(n-2)\times k$ So we need $n$ such that $48\mod (n-2)\equiv 0$ Of the shown above figures the only that doesn't follow this condition is $n=7$ , therefore the answer is the Heptagon.

In case of squares, if the number of squares is k, them its perimeter p1 is:

p1 = 2k + 2 = 50, 2K = 48, K = 24.

So in case of squares it is possible.

In case of pentagons, if their number is k, the its perimeter p2 is:

p2 = 3k + 2 = 50, 3k = 48, k = 16.

So in case of pentagons it is possible.

In case of hexagons, if their number is k, the its perimeter p3 is:

p3 = 4k + 2 = 50, 4k = 48, k = 12.

So in case of hexagons it is possible.

In case of heptagons, if their number is k, the its perimeter p4 is:

p4 = 5k + 2 = 50, 5k = 48, k = 9.8

So in case of heptagons it is not possible.

In case of octagons, if their number is k, the its perimeter p5 is:

p5 = 6k + 2 = 50, 6k = 48, k =8.

So in case of octagons it is possible.

In your chain the shapes have s sides and there are n shapes in the chain. (in the squares above, s=4, n=5 for example).

Now, each shape contibutes s-2 sides to the whole perimeter, except for the two ends which contribute an extra 1 each.

So p = n(s-2) + 2 or p-2 = n(s-2)

Now when can p be 50? When p-2 =48 n(s-2)=48 so (s-2) is a factor of 48. (s-2) can be 1,2,3,4 or 6 but NOT 5.

So s cannot be 7. Heptagons are impossible.

Let x be the number of segments of polygon and n be the number of polygons with x segments which are chained together

(x-1) * 2 + (x-2) * (n-2) = 50

2x-2 + nx – 2x – 2n + 4 = 50

Nx – 2n + 2 = 50

Nx – 2n = 48

1) X=4

4n – 2n = 48

2n = 48

n = 24

2) x = 5

5n – 2n = 48

3n = 48

n= 16

3) x=6

6n – 2n = 48

4n = 48

n = 12

4) x=7

7n – 2n = 48

5n = 48

n = 48/5 , not an integer .

5) x=8

8n – 2n = 48

6n = 48

n = 8

It can be seen that except for x=7, one can form a chain of n polygons with x sides with an overall perimeter of 50

Hence it is not possible to form a chain of heptagons with an overall perimeter of 50

The general formulas for the perimeter of each chain of n polygons are given by $P_{square}(n)=2n+2$ , $P_{pentagon}(n)=3n+2$ , $P_{hexagon}(n)=4n+2$ , $P_{heptagon}(n)=5n+2$ , and $P_{octagon}(n)=3n+2$ . Setting each equal to 50 and solving for n yields an integer solution for each chain except for the heptagons.