97 of 100: The Brothers Are Outnumbered

Let, $g$ be the number of girls in the family and $b$ be the number of boys.

In case-1, one girl has twice as many sisters as brothers. (Of course, she herself is not included as a sister!) So, $g-1=2b$

In case-2, one boy has five times as many sisters as brothers. (Again, the boy himself is not included as a brother!) Hence, $g=5(b-1)$

Subtracting the first equation from the second, we get $1=5(b-1)-2b \implies 1=3b-5 \implies b=2$

So, from the first equation, $g=1+2b=5$

Therefore, the total number of children is, $2+5=\boxed{7}$

Simple trial and error is fastest: From the first clause, there's at least 1 girl, so the minimum possible solution to the second clause is that a boy has 5 sisters and 1 brother. That also turns out to be a solution to the first clause so we're done.

[In fact, if we interpret "each of her brothers" to be vacuously true if there are no boys in line with the normal logical rules of the quantifier "forall", then 1 girl and 0 boys is also a valid solution. But clearly not what was intended given the other solution.]

Let $X$ be the number of girls. A girl has twice as many sisters as brothers, so the number of boys is $\frac{X-1}{2}$ . A boy has five times as many sisters as brothers, hence the family has $5 \left(\frac{X-1}{2}-1 \right)$ girls. Thus $X=5 \left(\frac{X-1}{2}-1 \right)$ and $X=5$ . Thus the number of children is $X+\frac{X-1}{2}=7$ .

Let the number of girls be x and the number of boys be y

Each girl has x-1 sisters and y brothers

x-1 =2y

x=2y+1

Each boy has X sisters and y-1 brothers

x=5(y-1)

= 5y-5

2y + 1 = 5y-5

3y=6

Y=2-number of boys

X = 2y+1

= 5 = number of girls

So the number of children in the family = 5+2 =7

There are five girls and 2 boys:

The girl has four sisters (not including herself) and two brothers. Four is twice as big as two.

The boy has one brother and five sisters. 5 is five times has big as 1.

Therefore, 5 sisters + 2 brothers equals 7 siblings.

Let 'G' be the number of girls and 'B' be the number of boys

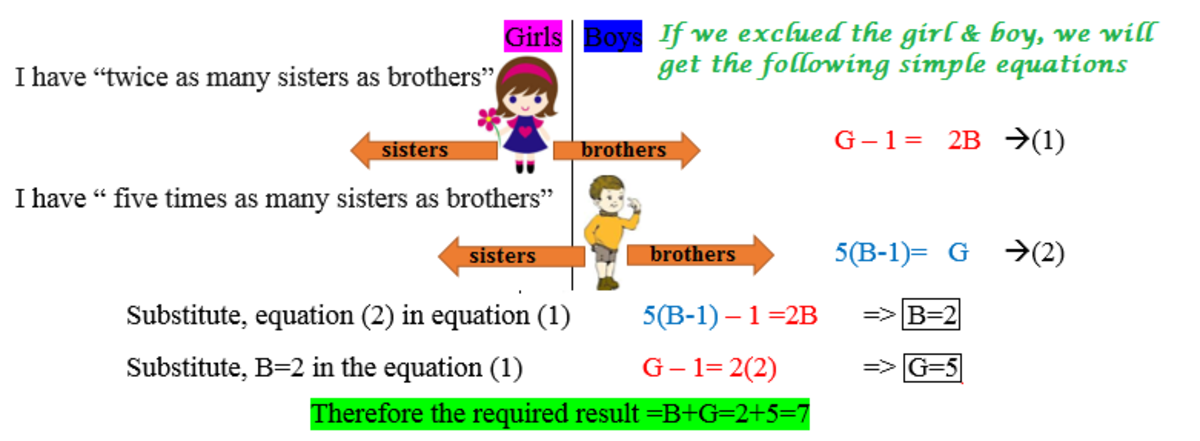
For each boy, number of sisters is five times the number of brothers, which means, the number of girls is in multiple of five, say 5n.
Then the number of boys is (5n/5)+1=n+1.
Total number of children=5n+(n+1)= 6n+1.
So, for each girl, the total number of (brothers+sisters) is 6n, which is in the ratio of 2:1 between girls and boys, i.e. 4n sisters and 2n brothers.
But, each girl has (5n-1) sisters,
So, 4n = 5n - 1, which gives n = 1, Total number of children=6n+1=7.

The number of girls has to be an odd number. This is because in order to have twice as many sisters as brothers (and be a girl) then you need to have an even number of sisters, and you count as a sister, making the number of girls an odd number. If you have twice as many sisters as brothers (and you are a boy) then the number of your sisters has to be divisible by 5. That means that the number of sisters can only be 5,15,25,35.... If you start with the least number that there could be (five) than you know that there would be 2 brothers because each sister has 4 sisters, and 2 is half of that. To each brother they would have (in this case) 1 brother and 5 sisters. That is 5 times as many sisters. If this didn't work, then you would have to try the other possible numbers too.

Case 1: Let the total no. of sisters the girl has be 2x Therefore total no. of brothers=x Thus, total no. of girls=2x+1.................(a) Total no. of children=2x+1+x=3x+1............(b) Case 2: The brother is speaking,hence no. of brothers this boy has=x-1 By question,no. of sisters this boy has=5(x-1)............(c) Therefore equating equations (a) and (c),we get, 5(x-1)=2x+1 x=2 From(b),total no. of children=7

I found my answer by drawing a flowchart of the relationships.

The number of girls is a multiple of 5, and one more than a multiple of 2; thus we look for odd multiples of 5, so that $g = 5, 15, 25, \dots$ Only $g = 5$ is realistic, and we see that it matches $b = 2$ nicely. There is no need to do any further work, unless one is not concerned with realism.

G G G G G - Five (Girls)

B B --------- Two (Boys)

Seven Children.

Each "G" has 4 sisters and 2 brothers satisfying the twice as many sisters as brothers requirement. Each "B" has 5 sisters and 1 brother satisfying the five times as many sisters as brothers requirement.

(PERSONAL NOTE:) I grew up in a family with multiple children:

I had twice as many sisters as brothers.

Each of my sisters had the same number of sisters as brothers.

What is a solution to the number of girls and boys in my family?

Since this describes my family exactly, I didn't need to do any formulas. I have 4 sisters and 2 brothers, and each of my brothers has 5 sisters and 1 brother.