DC Current Splitting with Transient
This circuit has the same steady-state behavior as the circuit from the previous problem , but with some transient behavior prior to that.
A D C voltage source V S and a D C current source I S feed a circuit with resistors R 1 and R 2 , inductor L , and capacitor C as shown. At time t = 0 , the inductor and capacitor are de-energized. Currents I R 1 ( t ) and I R 2 ( t ) flow in resistors R 1 and R 2 , respectively.
Determine the value of the quantity Q .
Q = ∫ 0 ∞ ( I R 1 ( t ) − I 0 ) d t + ∫ 0 ∞ ( 4 I 0 − I R 2 ( t ) ) d t
Details and Assumptions:
1)
V
S
=
1
0
volts
2)
I
S
=
5
amps
3)
R
1
=
2
Ω
4)
R
2
=
3
Ω
5)
L
=
5
0
H
6)
C
=
1
F
7)
I
0
=
1
amp
8)
Source and current polarities are as indicated in the diagram
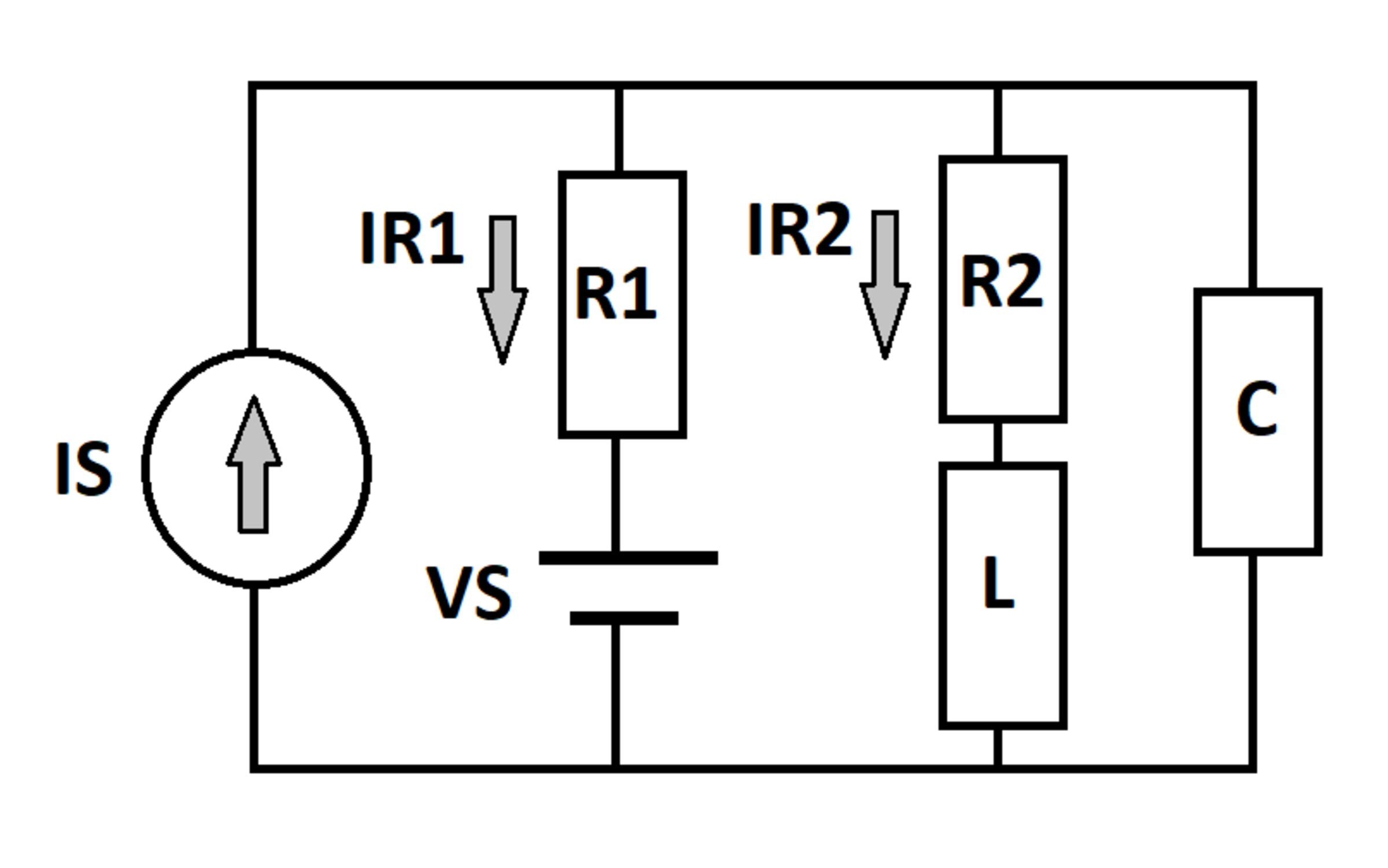
The answer is 77.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Luckily revisited my solution only to see a more interesting one. Thank you for sharing
You're welcome! Hope there were no other prerequisites for the "Final Value Theorem" - guess I'll have to double-check.
Edit: Seems there are no further prerequisites.
Let I 1 = I R 1 and I 2 = I R 2 . Let the charge on the capacitor be Q c and the current through it be I c at a general time t . Applying Kirchoff's laws gives the circuit equations:
− 1 0 − 2 I 1 + 3 I 2 + 5 0 I ˙ 2 = 0 5 0 I ˙ 2 + 3 I 2 = Q c I S = 5 = I 1 + I 2 + Q ˙ c
Simplifying the equations a bit more leads to the system of ODEs:
2 Q ˙ c + 5 0 I ˙ 2 = − 5 I 2 + 2 0 5 0 I ˙ 2 = − 3 I 2 + Q c
I 2 ( 0 ) = Q c ( 0 ) = 0
Taking Laplace transform on both sides and solving for I 2 ( s ) and I c ( s ) knowing that I c ( s ) = s Q c ( s ) :
I 2 ( s ) = s ( 1 0 0 s 2 + 5 6 s + 5 ) 2 0 I c ( s ) = ( 1 0 0 s 2 + 5 6 s + 5 ) 2 0 ( 5 0 s + 3 ) ∵ 5 = I 1 + I 2 + Q ˙ c
Now computing the inverse Laplace transform using Wolfram leads to the following. Let:
a = − 2 5 7 − 5 0 7 1 b = − 2 5 7 + 5 0 7 1
I 2 ( t ) = 7 1 2 ( ( − 7 1 + 1 4 7 1 ) e a t − ( 7 1 + 1 4 7 1 ) e b t + 1 4 2 ) I c ( t ) = 7 1 5 ( ( 1 1 + 7 1 ) e a t + ( 7 1 − 1 1 ) e b t ) ∵ 5 = I 1 + I 2 + Q ˙ c ∴ I 1 ( t ) = 5 − I 2 ( t ) − I c ( t )
After having obtained these closed form expressions, the next step is to evaluate the required integrals which also have a closed form:
∫ 0 ∞ ( 4 − I 2 ( t ) ) d t = ∫ 0 ∞ ( 4 − 7 1 2 ( ( − 7 1 + 1 4 7 1 ) e a t − ( 7 1 + 1 4 7 1 ) e b t + 1 4 2 ) ) d t ∫ 0 ∞ ( I 1 ( t ) − 1 ) d t = ∫ 0 ∞ ( 5 − 7 1 2 ( ( − 7 1 + 1 4 7 1 ) e a t − ( 7 1 + 1 4 7 1 ) e b t + 1 4 2 ) − 7 1 5 ( ( 1 1 + 7 1 ) e a t + ( 7 1 − 1 1 ) e b t ) − 1 ) d t
I did not even consider touching these manageable but very tedious monsters. Numerically evaluating leads to:
Q = ∫ 0 ∞ ( I 1 ( t ) − 1 ) d t + ∫ 0 ∞ ( 4 − I 2 ( t ) ) d t ≈ 7 7 . 6
You can use the final limit theorem to avoid inverse Laplace-Transforms and integration at the same time! Before we begin, we normalize all currents, voltages, time and elements by the values given below: voltages: 1 V , currents: 1 A , time: 1 s ⇒ R : 1 Ω , C : 1 F , L : 1 H , Q : 1 C The network equations remain the same in the process, but now all currents, voltages, time and elements represent their normalized dimensionless counterparts.
After switching ( t ≥ 0 )
The network was de-energized at t = 0 − , so all initial conditions at t = 0 − vanish and i R 1 , 2 ( t ) only depend on the input sources v s ( t ) , i s ( t ) . To calculate the two currents efficiently with Laplace-Transforms, we define the voltage u C ( t ) over C from top to bottom. With KVL, we get V s ( s ) = s 1 0 , I s ( s ) = s 5 ⇒ I R 1 ( s ) = R 1 U C ( s ) − V s ( s ) = 2 U C ( s ) − s 5 , I R 2 ( s ) = s L + R 2 U C ( s ) = 5 0 s + 3 U C ( s ) To calculate U C ( s ) , we combine R 1 , V s ( s ) into an equivalent current source and use superposition afterwards: U C ( s ) = ( ( s L + R 2 ) ∥ R 1 ∥ s C 1 ) ⋅ ( I s ( s ) + R 1 V s ( s ) ) = s + 2 1 + 5 0 s + 3 1 1 ⋅ ( s 5 + s 5 ) = s 2 + 0 . 5 6 s + 0 . 0 5 s + 0 . 0 6 ⋅ s 1 0 We calculate the Laplace-Transforms of both integrands. The poles at s = 0 cancel out, i.e. I 0 , 4 I 0 are the steady-state currents i R 1 , 2 ( t ) will converge to: I R 1 ( s ) − s I 0 s 4 I 0 − I R 2 ( s ) = 2 U C ( s ) − s 6 = ( s 2 + 0 . 5 6 s + 0 . 0 5 ) s − 6 s 2 + 1 . 6 4 s = s 2 + 0 . 5 6 s + 0 . 0 5 − 6 s + 1 . 6 4 = s 4 − 5 0 s + 3 U C ( s ) = ( s 2 + 0 . 5 6 s + 0 . 0 5 ) s 4 s 2 + 2 . 2 4 s = s 2 + 0 . 5 6 s + 0 . 0 5 4 s + 2 . 2 4 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ s 1 , 2 = − 2 5 7 ± 6 2 5 4 9 − 2 0 1 = − 2 5 7 ± 5 0 7 1 < 0 Both remaining poles s 1 , 2 lie in the open left plane, so we may use the Final Value Theorem to calculate both parts of Q together: Q = s → 0 lim s ⋅ s 1 ( I R 1 ( s ) − s I 0 + s 4 I 0 − I R 2 ( s ) ) = s → 0 lim s 2 + 0 . 5 6 s + 0 . 0 5 − 2 s + 3 . 8 8 = 0 . 0 5 3 . 8 8 = 7 7 . 6
Rem.: This way is efficient if you're only interested in the value of Q , but not the transients i R 1 , 2 ( t ) For the transients, there is no way around partial fraction decomposition (PFD) and inverse Lapace-Transform :(