DC Current Splitting

Electricity and Magnetism Level 1

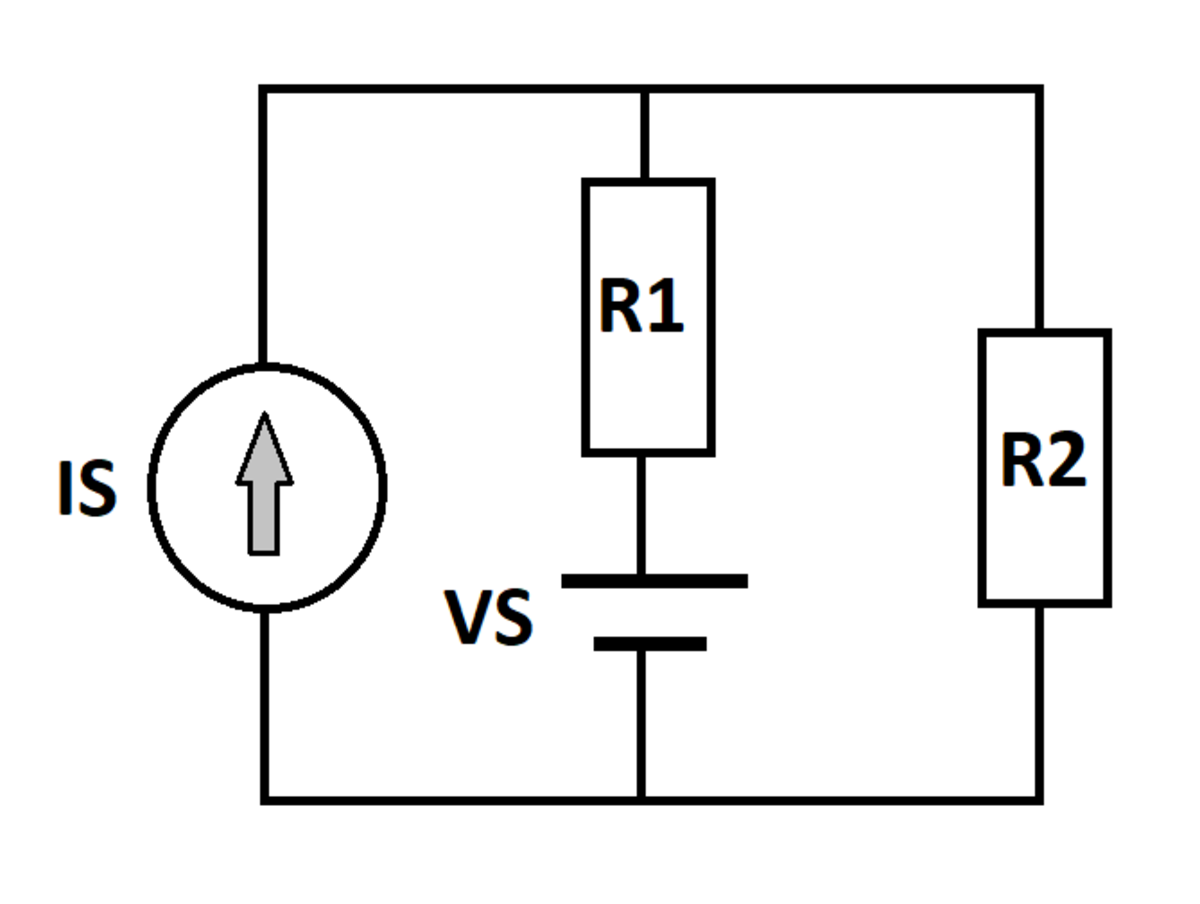
A $DC$ voltage source $V_S$ and a $DC$ current source $I_S$ feed a circuit with resistors $R_1$ and $R_2$ as shown. What is the current through $R_2$ ?

Details and Assumptions:
1) $V_S = 10$ volts
2) $I_S = 5$ amps
3) $R_1 = 2 \Omega$
4) $R_2 = 3 \Omega$
5) Give your answer as a positive number
6) Source polarities are as indicated in the diagram

The answer is 4.0.

2 solutions

Tom Engelsman
May 11, 2021

Let $V_{0}$ be the potential at the top-center node above resistor $R_{1}.$ Applying KCL at this node yields the relationship:

$\Large I_{S} = I_{R1} + I_{R2} = \frac{V_{0}-V_{S}}{R_{1}} + \frac{V_{0}}{R_{2}}$

and solving for $V_{0}$ produces:

$\Large (I_{S} + \frac{V_{S}}{R_{1}})(\frac{R_{1}R_{2}}{R_{1}+R_{2}}) = V_{0}$ ;

or $\Large (5 + \frac{10}{2})(\frac{2 \cdot 3}{2+3}) = V_{0};$

or $V_{0} =12$ volts. Finally, $\large I_{R2} = \frac{V_{0}}{R_{2}} = \frac{12}{3} = \boxed{4}$ amps.

Veeresh Pandey
May 13, 2021

Use current division and superposition

DC Current Splitting

The answer is 4.0.

2 solutions

0 pending reports