Dead functions

A smooth function is a function which is differentiable forever, i.e, both it and all of it's derivatives are defined and continuous.
A flat function is a smooth function which has a point, where all of the derivatives of the function go to zero. 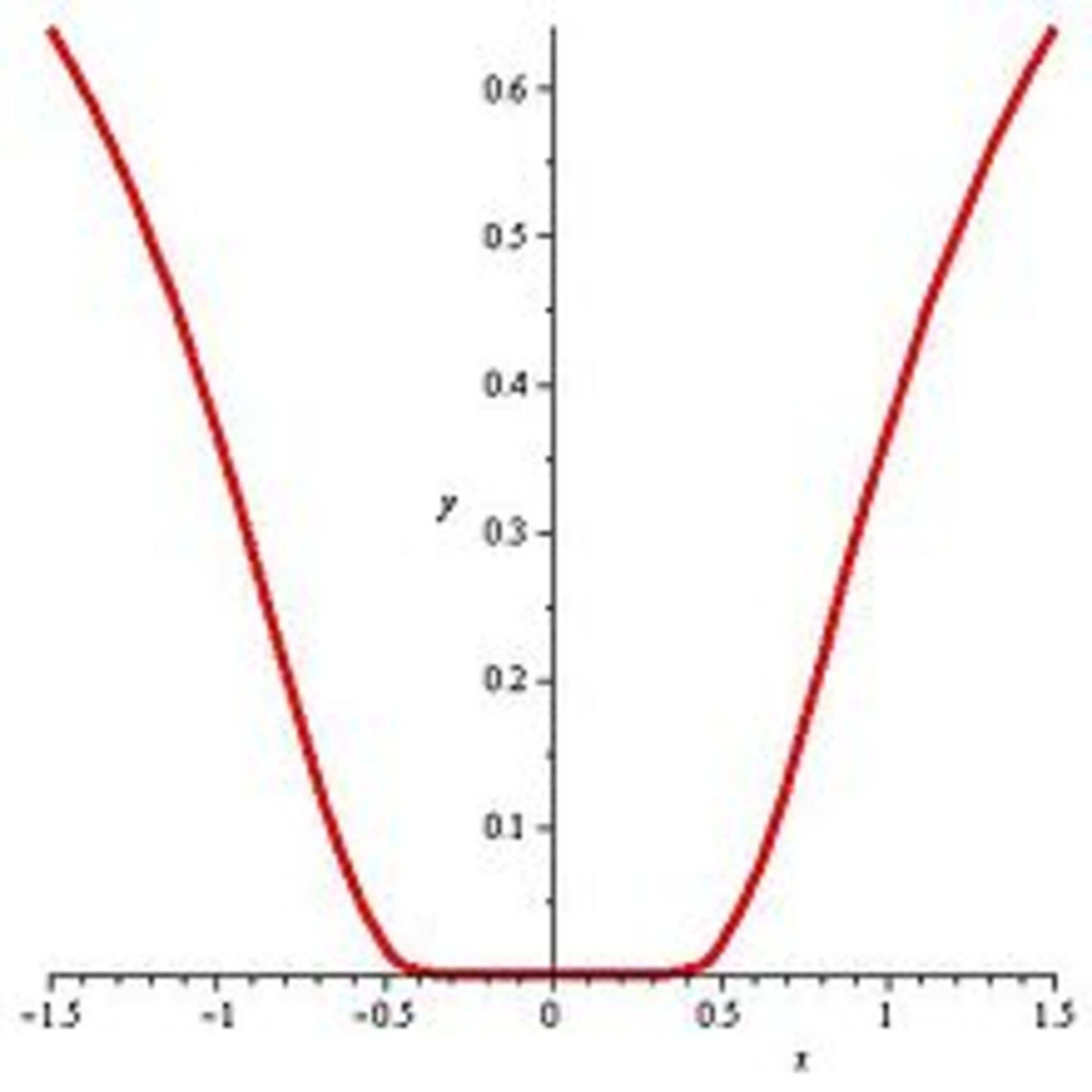$y=e^{-\frac{1}{x^2}}$ is flat at x=0.

In the example above, as x approaches zero, every derivative of the function (and in this case, the function itself, but that is not necessary) approaches zero.

Notice that the function is not defined at x=0, so it doesn't actually have a point where all of it's derivatives equal zero, only a point where they go to zero. Let's define a dead function as a function which is flat at a defined point, i.e, it has a point where all derivatives actually equal zero.

It's obvious that all constant functions (of the form $y=c$ ) are dead, but is that it? Can a non-constant dead function exist?

(Note: For our purposes, a piecewise function made of two different smooth functions cannot be smooth at the point of meeting, and thus, cannot be dead at that point).

Solutions/Proofs welcome!