Deadlock Cats and Dogs
There are two neighbors Adam and Brian. Adam owns a cat while Brian owns a dog. Sometimes, they need to walk their pets in the park. However, only one of them can do so at any point in time as their pets don’t get along.
They arrive at an agreement to decide who gets to go to the park. There is a wooden arrow pointing at either house that both of them can control. Anyone who wants to go to the park will do the following:
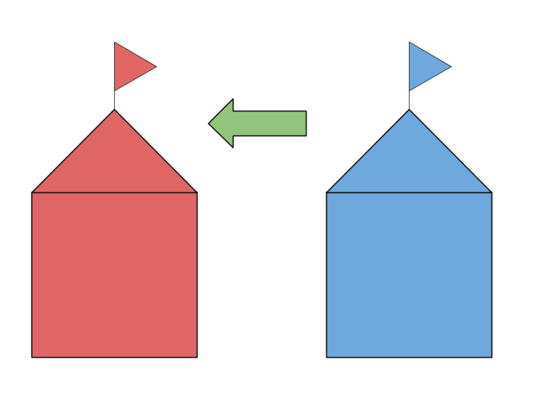1. Set the wooden arrow pointing to the other house.
2. Raise a flag on their terrace.
3. Wait until the other flag is lowered or the arrow is pointing to his own house.
4. Go for a walk in the park.
5. Come back and lower the flag.
Does this procedure guarantee that Adam and Brian won't walk their pets in the park simultaneously?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
While the order suggests that it should not be possible for Adam and Brian to walk their pets in the park simultaneously, the timing of events (and the absence of a temporary local lock on the arrow between 1 and 2) can allow it. This is called a Race Condition .
Consider the scenario in the table below, which does not contain context for why there is a timing issue between procedures.
Both Adam's and Brian's flags start in the down position.
Each entry in a row represents a successfully executed procedural event.