Dealing with Reflections and Refractions.
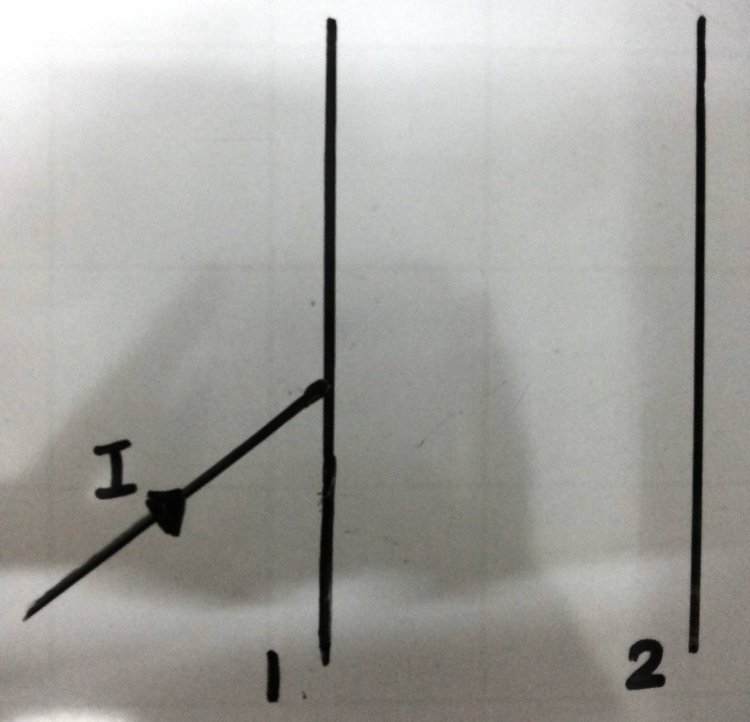 A narrow monochromatic beam of light of intensity
I
is incident on a glass plate as shown in figure. Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects 25% and transmits the remaining. Find the ratio of maximum and minimum intensities (i.e.,
) in the interference pattern formed by the two beams obtained after one reflection at each plate.
A narrow monochromatic beam of light of intensity
I
is incident on a glass plate as shown in figure. Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects 25% and transmits the remaining. Find the ratio of maximum and minimum intensities (i.e.,
) in the interference pattern formed by the two beams obtained after one reflection at each plate.
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each plate reflects 25% and transmits(refracts) 75% .
Intensity of incident ray (Initial intensity I ) after each reflection and refraction is shown in figure.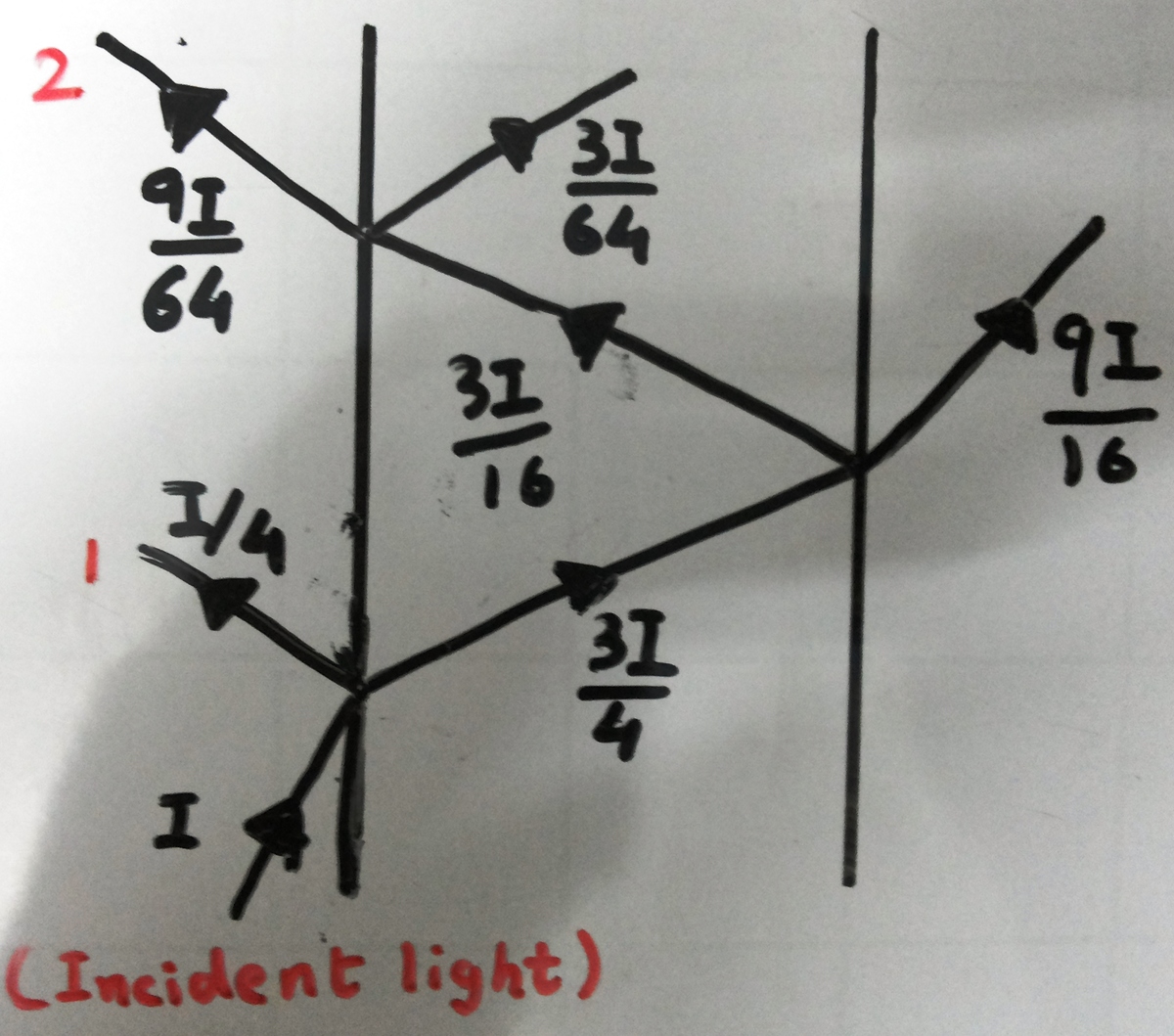
Interference pattern will take place in between rays 1 and 2 .
⇒ I 1 = 4 I a n d I 2 = 6 4 9 I
∴ I m i n I m a x = ( I 1 − I 2 I 1 + I 2 ) 2 = 1 4 9 = 4 9