Decagon in a Pentagon
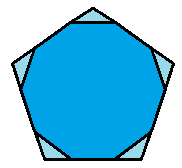
Every other side of a regular decagon is extended to form a regular pentagon.
If A d is the area of the decagon and A p is the area of the pentagon, then ( A p A d ) 2 = b a , where a and b are relatively prime positive integers.
Find a + b .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice problem and solution.
In the diagram below, O is the centre of the decagon (and of the pentagon) and A is the midpoint of one of the sides of the pentagon. B and C are vertices of the decagon and pentagon.
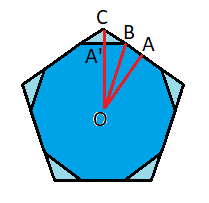
The required ratio of the areas is A p A d = △ O A C △ O A B + △ O A ′ B = △ O A C 2 △ O A B = A C 2 A B , where the last relation holds as triangles O A B and O A C share the side O A , and B is on A C .
But A B = O A ⋅ tan 1 8 ∘ and A C = O A ⋅ tan 3 6 ∘ ; so the ratio we want is just tan 3 6 ∘ 2 tan 1 8 ∘ = 5 2 (using standard trig results for angles in a pentagon) giving the answer 2 2 + ( 5 ) 2 = 9 .
Nice solution! I believe you have an extra square on the 5 of the last equation.
Yep, certainly did - fixed now, thank you!
The function inRadius computes the incircle of a n-sided regular polygon giving that the vertices are on a circle of radius of 1. The function uses the area of a triangle formula where the length of a single edge is the base and the desired inRadius is the altitude of the triangle.
inRadius = FullSimplify [ EuclideanDistance @@ Take [ CirclePoints [ { 0 , 0 } , { 1 , 0 } , $#$1 ] , 2 ] 2 Area [ Triangle [ Join [ Take [ CirclePoints [ { 0 , 0 } , { 1 , 0 } , $#$1 ] , 2 ] , ( 0 0 ) ] ] ] ] & ;
The inRadii are used to scale the two polygons so that they have the same inRadii. The ratio of their areas is computed and the expression is simplified.
FullSimplify [ ( Area [ Polygon [ CirclePoints [ { 0 , 0 } , { inRadius ( 1 0 ) , 1 0 π } , 5 ] ] ] Area [ Polygon [ CirclePoints [ { 0 , 0 } , { inRadius ( 5 ) , 0 } , 1 0 ] ] ] ) 2 ] ⇒ 5 4
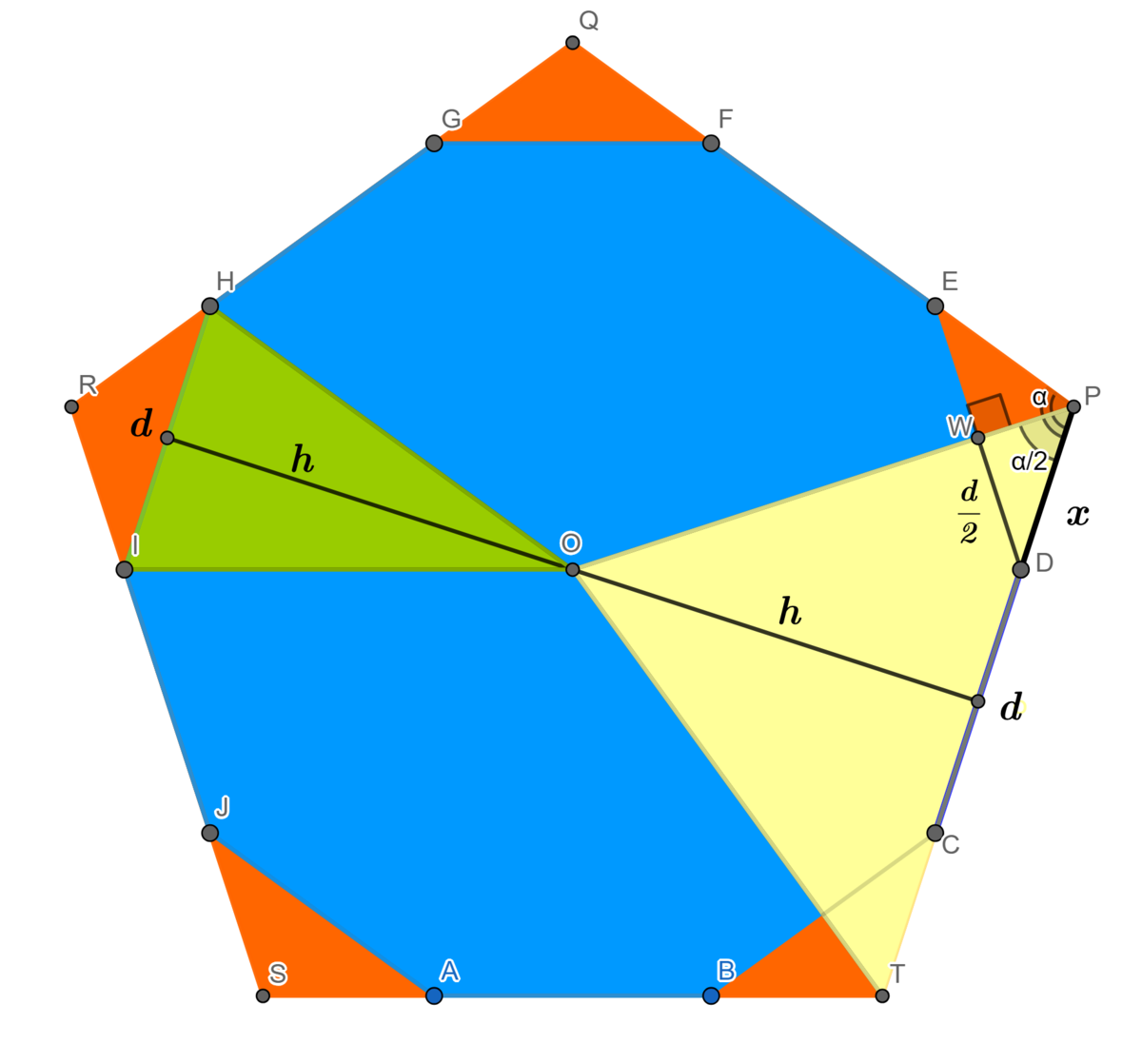
We have, Area of the decagon Area of the pentagon Now, Area ( Δ O I H ) Area ( Δ P O T ) Consider Δ P W D sin 2 α ⟹ 2 x ⟹ ( d + 2 x ) ( Area of the pentagon Area of the decagon ) 2 ⟹ a + b In the above figure ABCDEFGHIJ is a decagon inscribed in the pentagon PQRST,O is their common center. = 1 0 × Area ( Δ O I H ) = 5 × Area ( Δ P O T ) = 2 1 d h h is the height = 2 1 ( d + 2 x ) h = 2 x d Where α is the interior angle of a regular pentagon = 1 0 8 ∘ = sin 2 α d = sin 5 4 ∘ d = 4 5 + 1 d , sin 5 4 ∘ = 4 5 + 1 = ( 5 + 1 4 + 1 ) d = ( ( 5 − 1 ) + 1 ) d = 5 d = ( 5 × Area ( Δ P O T ) 1 0 × Area ( Δ O I H ) ) 2 = ⎝ ⎜ ⎛ 5 × 2 1 ( d + 2 x ) h 1 0 × 2 1 d h ⎠ ⎟ ⎞ 2 = ( 5 d h 2 d h ) 2 = ( 5 2 ) 2 = 5 4 = 9
Nice solution! Thanks for sharing it.
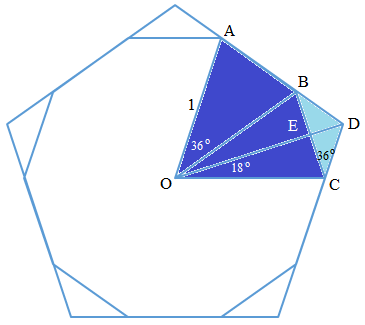
Since we are dealing with ratio, we need only consider one-fifth of the two regular polygons as shown in the figure.
A p A d = [ O A D C ] [ O A B C ] = [ O B C ] + [ C D E ] [ O B C ] = 2 1 sin 3 6 ∘ + 2 1 C E × D E 2 1 sin 3 6 ∘ = sin 3 6 ∘ + sin 2 1 8 ∘ tan 3 6 ∘ sin 3 6 ∘ = 1 + cos 3 6 ∘ sin 2 1 8 ∘ 1 = cos 3 6 ∘ + 2 1 ( 1 − cos 3 6 ∘ ) cos 3 6 ∘ = 1 + cos 3 6 ∘ 2 cos 3 6 ∘ = 5 + 5 2 ( 1 + 5 ) = 5 2 where [ ⋅ ] denotes the area of ⋅ , Let O B = O C = 1 See note: cos 3 6 ∘ = 4 1 + 5
Therefore, ( A p A d ) 2 = ( 5 2 ) 2 = 5 4 ⟹ a + b = 4 + 5 = 9 .
Note:
cos 5 π + cos 5 3 π cos 5 π − cos 5 2 π 2 cos 5 π − 2 ( 2 cos 2 5 π − 1 ) 4 cos 2 5 π − 2 cos 5 π − 1 ⟹ cos 5 π = 4 1 + 5 = 2 1 = 2 1 = 1 = 0
Nice solution! I believe near the end a minus sign should be an equal sign (so it should say 5 + 5 2 ( 1 + 5 ) = 2 2 ).
The decagon and the pentagon share the same apothem, and the area of a regular polygon with n sides and an apothem a is A = n a 2 tan ( n 1 8 0 ° ) , so A d = 1 0 a 2 tan ( 1 0 1 8 0 ° ) = 1 0 a 2 5 5 − 2 5 and A p = 5 a 2 tan ( 5 1 8 0 ° ) = 5 a 2 5 − 2 5 .
Therefore, ( A p A d ) 2 = ( 5 a 2 5 − 2 5 1 0 a 2 5 5 − 2 5 ) 2 = 5 4 , so a = 4 , b = 5 , and a + b = 9 .