Decent Geo/NT/Pythagorean Problem
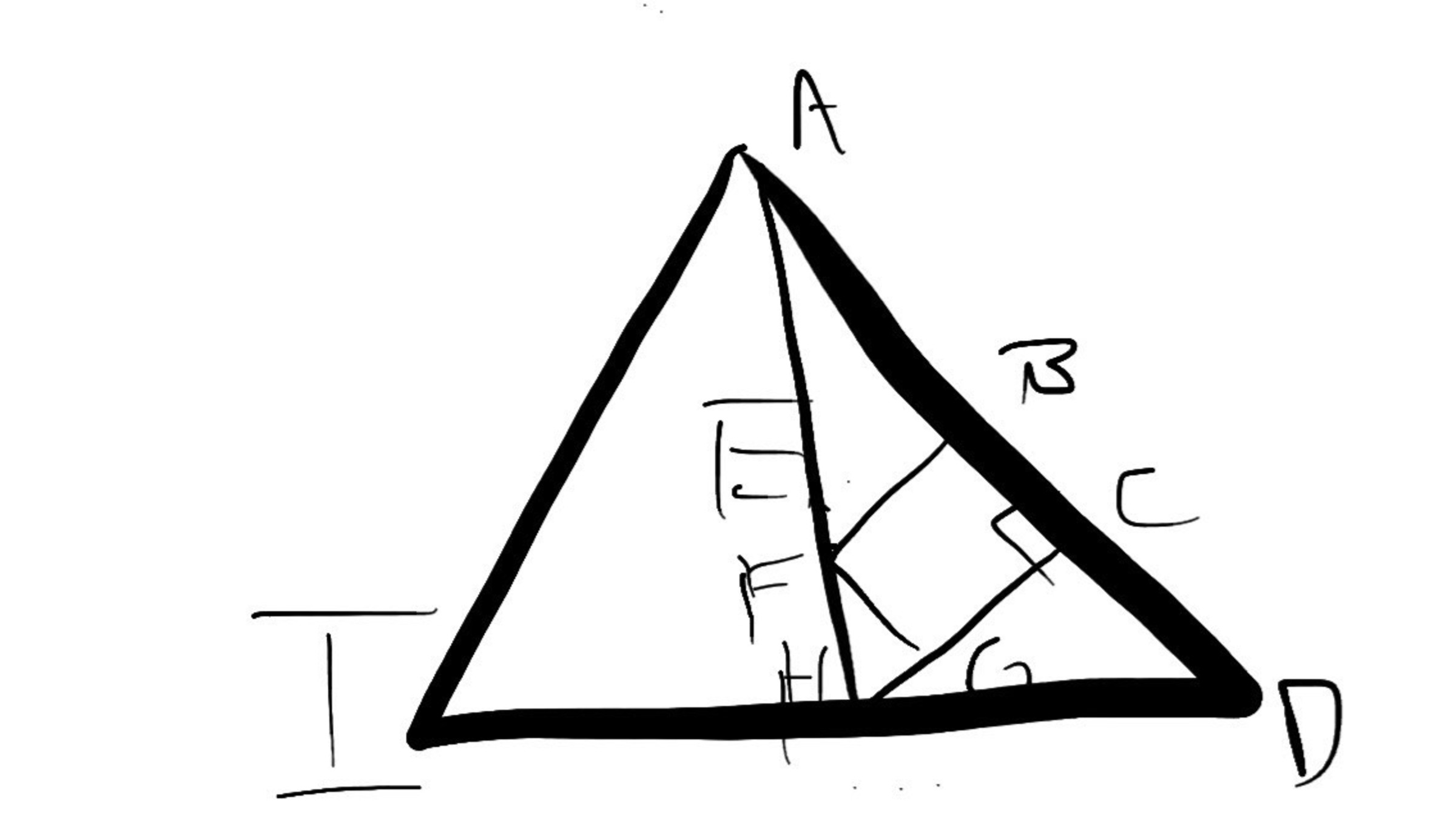
ACH is a right triangle with all sides relatively prime and integers. AC is even. Construct triangle AID such that AH is triangle AID's median. E is the centroid of triangle AID. F is on AC such that BCGF is a square. How many values of AC can there be if F is between H and E, and AC 200?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly, notice how AE/EH is 2:1, as that's what a centroid does ( Centroid is the intersection of medians ). Now, IF F was E, then the ratios of areas of triangles AEC and HEC would be 2:1 respectively. If F is between H and E, that means that the ratio of AFC: HFC is greater than 2. FB = FG as they are sides of a square. They are both altitudes of AFC and HFC respectively. That means that AC:HC > 2:1.
This means the problem is effectively asking - how many primitive pythagorean triples are there such that the even leg is less than 200 and more than twice as long as the odd leg.
You can parametrize pythagorean triples as so, where m and n are relatively prime positive integers:
2mn, m 2 +n 2 , and m 2 -n 2 . Therefore the problem is asking to find how many values for 2mn there are where: mn > m 2 -n 2 .
Taking mn to the other side yields 0 > m 2 + mn - n 2 . Assuming it is = 0, solving the quadratic yields that m = n(1 + 5 which is ~ 1.62n. This is considering the equation to be equal to 0. It must be less than 0. So m must be less than 1.62n. Now the final step:
Note that m must be:
- 1. Greater than n, and integer, and less than 1.62n, meaning it must be at least 2.
- 2. Relatively prime to n, and if N is odd, M must be even, as m 2 -n 2 must be odd.
- 3. mn<100
N can max be 9, as 10 2 + 11 2 > 200. If N = 1, then M must be less than 1.62, and that is 1. This isn't possible for rule 1. If N = 2, M = 3; N = 3, M = 4; N = 4, M = 5; N = 5, M = 6 OR 8; N = 6, M = 7; N = 7, M = 8 OR 10; N = 8, M = 9 OR 11; N = 9, M = 10.
These are 11 Cases, so that is the problem SOLVED!