Deceptively Complex
Computer Science
Level
2
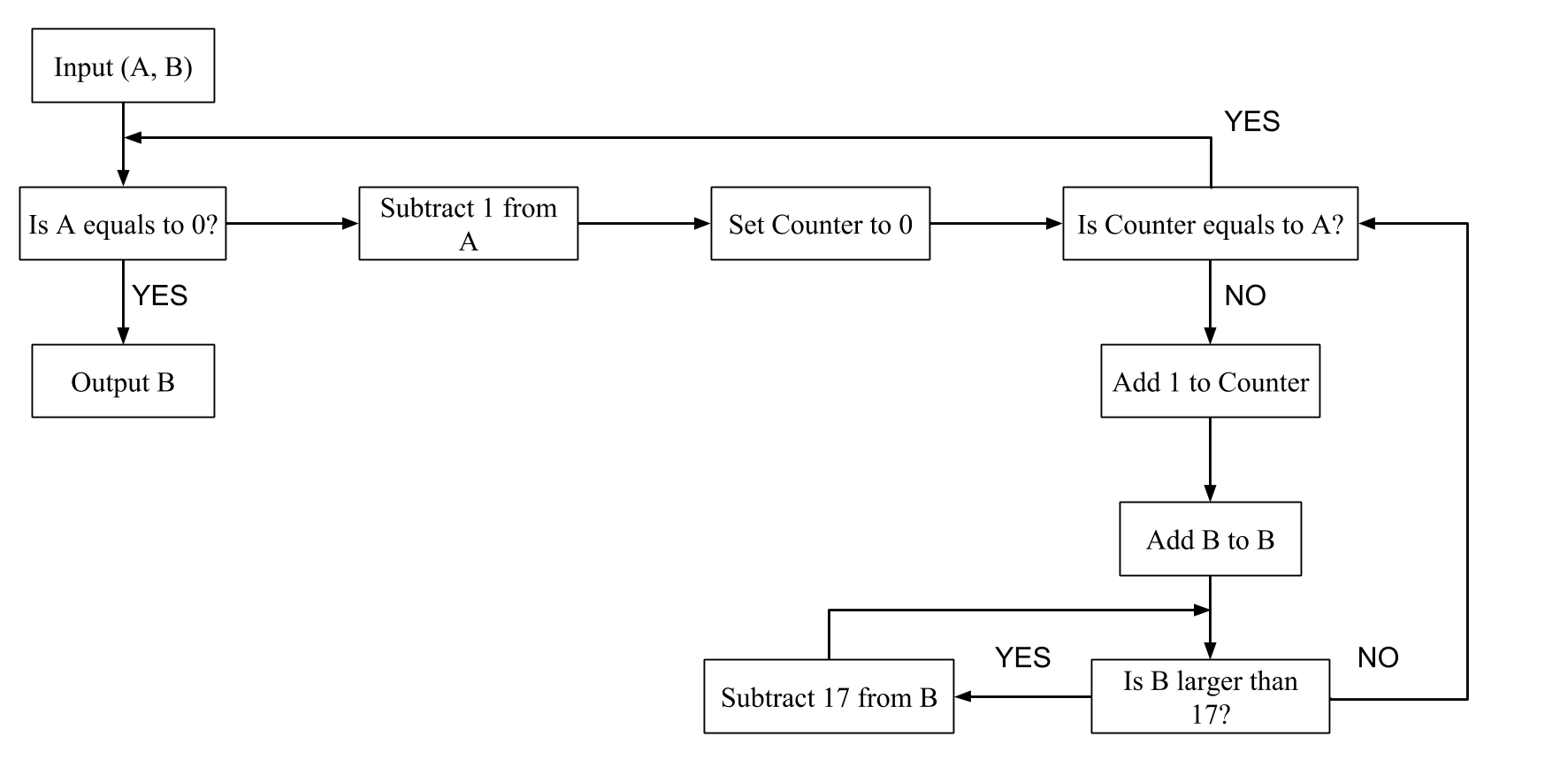
What will the above process output when we pass the input as ?
1
2
3
4
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The idea is to break down this process into several subprocesses.
Take a look at the bottom right corner. It keeps subtracting 17 from B when B is larger than 17, this will in the end return B m o d 1 7 , except when the result is 0, it will return 17.
Now, let's look at the process that starts from Set Counter to 0 . The process after this will be repeated A times. More precisely, we perform Add B to B for A times. Add B to B is another way of saying Multiply B by 2 . So the entire process will multiply B by 2 A .
Again, the whole process keeps repeating for A = 6 , 5 , 4 , 3 , 2 , 1 . Hence, B is multiplied by 2 for 5 + 4 + 3 + 2 + 1 + 0 times. B becomes
B × 2 5 × 2 4 × 2 3 × 2 2 × 2 1 = B × 2 1 5 = 2 2 × 2 1 5 = 2 1 7
Recall that we keep subtracting 1 7 from B, and we know that a n m o d b = ( a m o d b ) n m o d b , so it doesn't matter if we do the modulo first or multiplication first. Finally, by Fermat's Little Theorem ,
2 1 7 m o d 1 7 = 2 .