Decomposing Regular Polyhedra

Geometry Level 4

For which regular polyhedra can you partition the vertices of the Polyhedra into some sets of 4 vertices such that each for each set of the 4 vertices, if we join every vertex to every other, we get a regular tetrahedron.

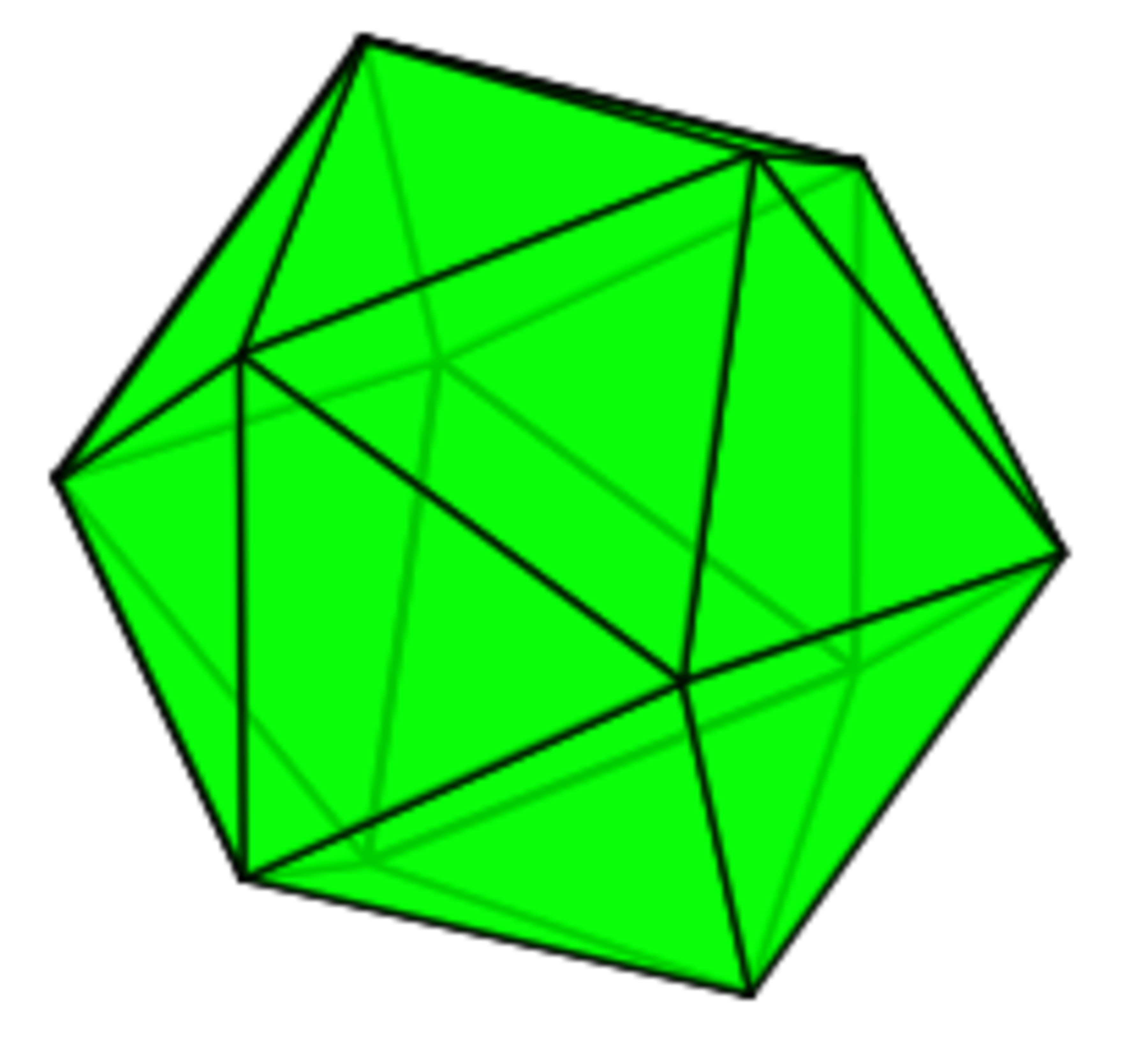
(A) : Icosahedron

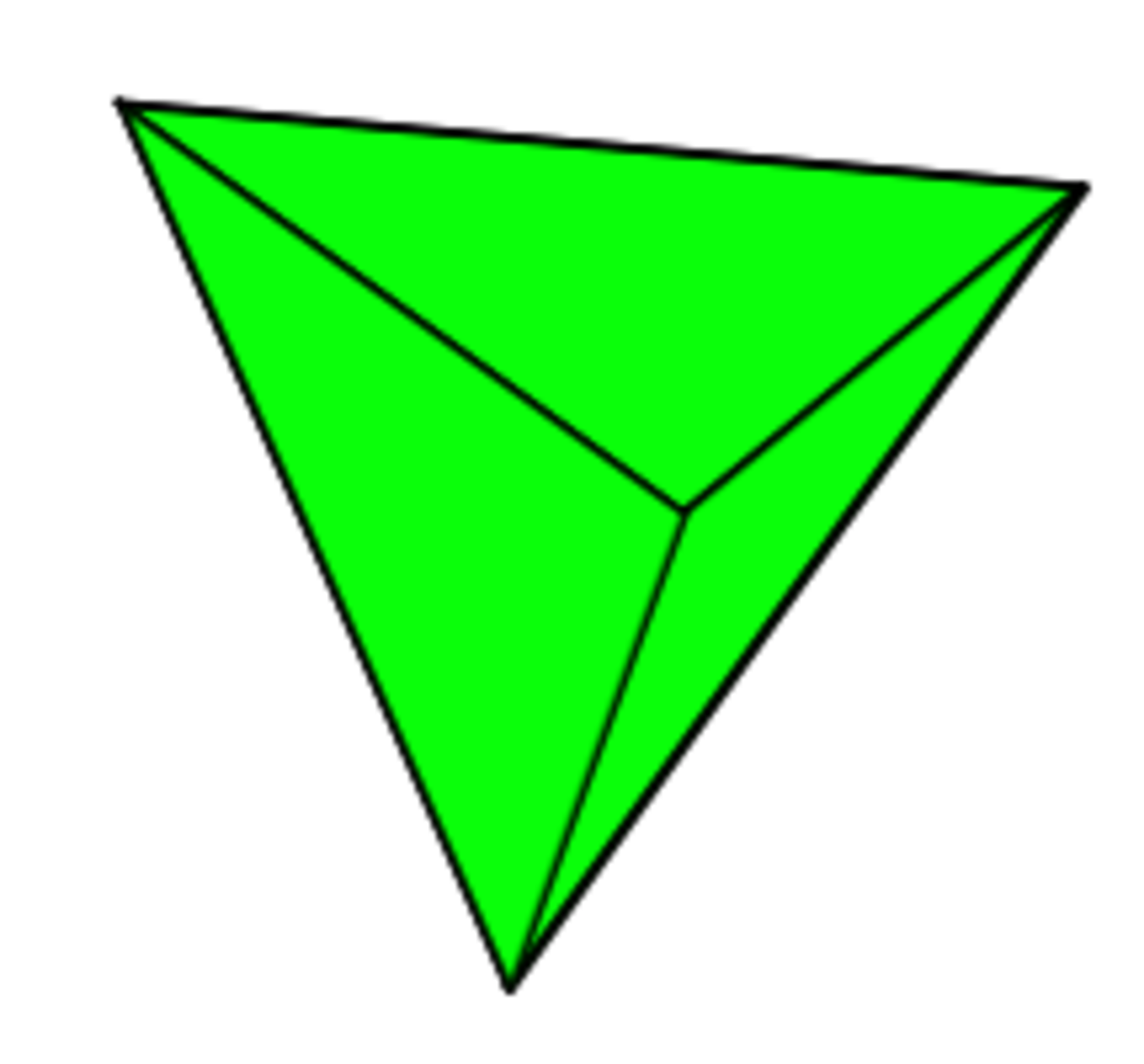
(B) : Regular Tetrahedron

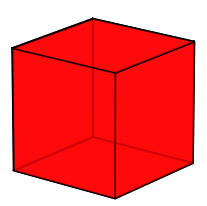
(C) : Cube

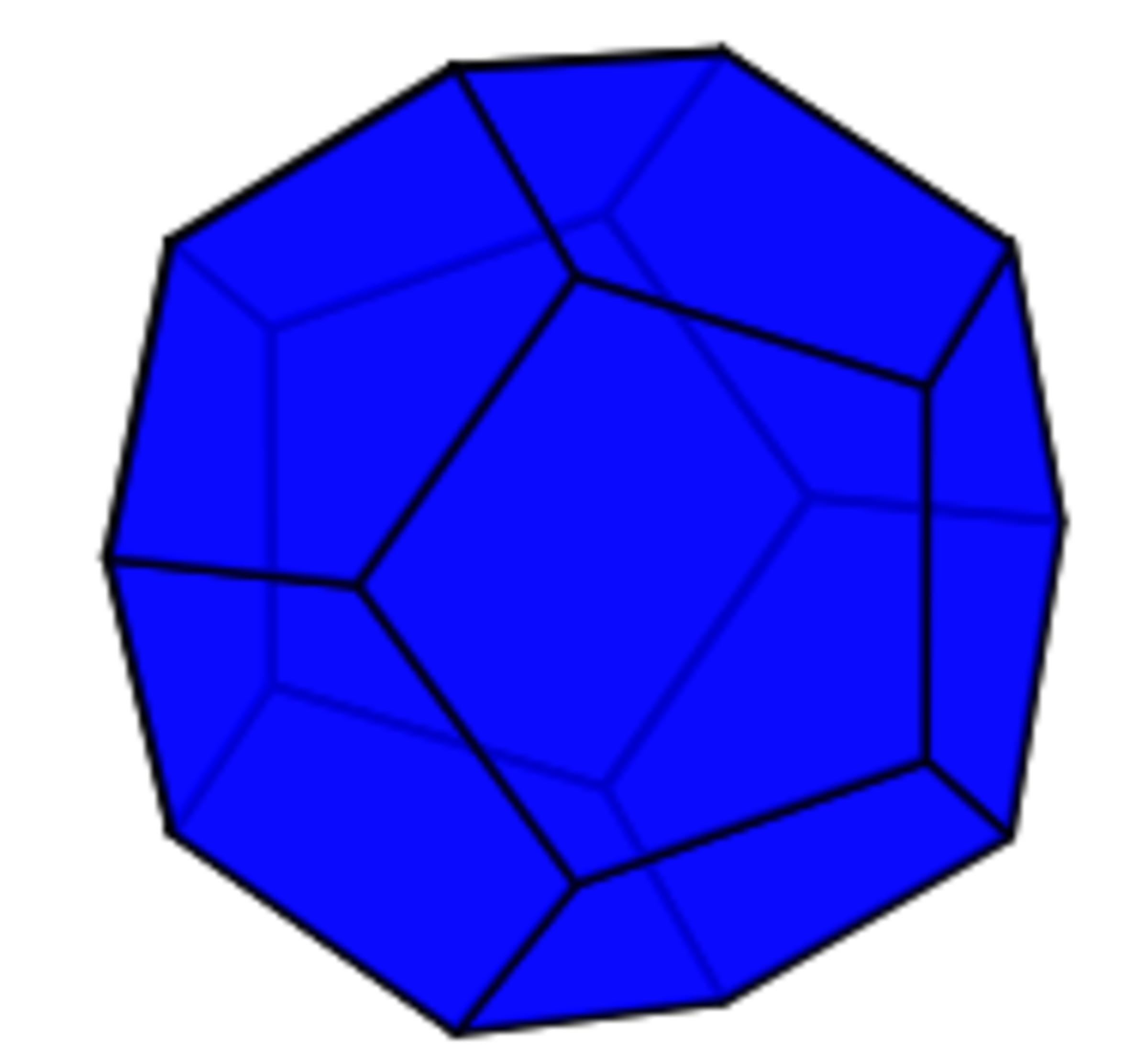
(D) : Dodecahedron

(E) : Octahedron

A, B, C A, B, C , D, E B, C, D A, B, C , D A, C, D D, E

Roberto Nicolaides by Roberto Nicolaides , 26, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Anand Chitrao
Aug 14, 2016

Suppose a polyhedron can be partitioned into sets of 4 vertices say S1, S2,..., Sk. Then for each set Si, joining each vertex in Si to every other vertices in Si is creating a complete graph on 4 vertices which is precisely a tetrahedron. So we cont the regular polyhedra which have number of vertices, a multiple of 4. Those are B, C and D.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Hi Anand,

Nice observation :)

I realise I did not put regular tetrahedron into the question ( I have edited this in now )! Can you see what the answer is if we add this new restraint?

And note that the icosahedron has 12 vertices.

Roberto Nicolaides - 4 years, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...