Deduce The Weight Of A Truck From Its Flat Tires
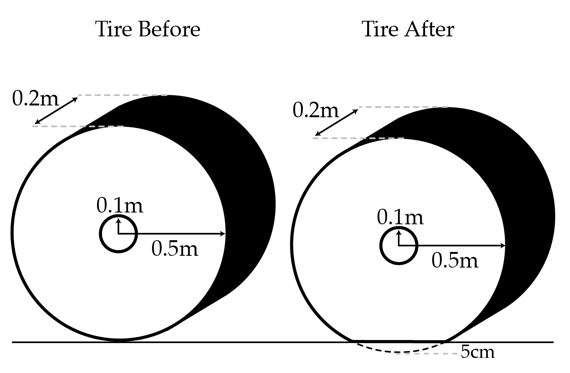 Four rubber tires of outer radius 0.5 m, inner radius 0.1 m, and width 0.2 m are inflated with air to a gauge pressure of 200 kPa. The tires are then attached to a truck and the truck is placed on the ground at sea level. The bottom of the tires very quickly squish by 5 centimeters but the tires retain their shape otherwise. What is the total mass of the truck and tires in
kg
?
Four rubber tires of outer radius 0.5 m, inner radius 0.1 m, and width 0.2 m are inflated with air to a gauge pressure of 200 kPa. The tires are then attached to a truck and the truck is placed on the ground at sea level. The bottom of the tires very quickly squish by 5 centimeters but the tires retain their shape otherwise. What is the total mass of the truck and tires in
kg
?
Details:
The acceleration due to gravity is
−
9
.
8
m
/
s
2
.
The truck's weight is distributed equally on all four tires.
Assume air is completely made up of
O
2
and
N
2
. (Hint: This information is necessary for this problem.)
Atmospheric pressure at sea level is 101.325 kPa.
You may neglect any 'surface tension' of the tires.
The answer is 11021.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Discussions for this problem are now closed
why did u take it as adiabatic plz explain.......
Nice problem!
There is a typo somewhere near the end...
CORRECTED STATEMENT:
The area on which this final pressure acts is,
A
=
0
.
2
×
2
0
.
5
2
−
0
.
4
5
2
=
0
.
0
8
7
1
7
7
9
m
2
v nice
shouldn't the area on which the final pressure will act be multiplied by 2....?? i mean A=0.2 * 2 * √(0.5^2-0.45^2 )
Could anyone please explain me where I have gone wrong. I conserved energy between the initial and final states. I considered the entire truck as a system.I am not listing the equations obtained by me in detail but just giving a fair idea of what I have tried. Since the process is an adiabatic one we have:
Work done by all external forces=change in internal energy of system Thus Work done by gravity+Work done by external atmospheric pressure=change in internal energy of the gas
The work done by the gas is simply the atmospheric pressure multiplied by the the reduction in volume.I also used the adiabatic relation T V γ − 1 = c o n s t a n t while calculating the change in internal energy of the gas. However I obtained a completely different answer. Please help! Any help will be greatly appreciated!
Hi Karthik, it is a little hard to see where you've gone wrong. Can you describe your work in some more detail? For instance, is there a particular point where you stop agreeing with Anish's solution?
First of all, let us calculate the Initial Volume.
Note: I shall leave the geometrical calculations to the reader.
V 1 = π ( 0 . 5 2 − 0 . 1 2 ) × 0 . 2 = 0 . 1 5 0 7 9 m 3
The change in volume is clearly the volume of the squisshed part (volume of the partial cylinder)
Δ V = A r e a × 0 . 2 = ( A s e c t o r − A t r i a n g l e ) × 0 . 2 = 2 . 9 3 6 3 × 1 0 − 3 m 3
⇒ V 2 = V 1 − Δ V = 0 . 1 4 7 8 6 m 3
Now comes the key part.
Note that the problem mentions that the process is very fast.
Immediately, Adiabatic process comes into our mind.
P V γ = C o n s t a n t
Also,
γ = f f + 2 , where f is the degree of freedom
Since the gas is diatomic ( O 2 and N 2 ),
f = 5
Thus,
γ = 5 7
We also know,
Total Pressure = Gauge Pressure + Atmospheric Pressure
P 1 = 1 0 1 . 3 2 5 + 2 0 0 k P a = 3 0 1 3 2 5 P a
Using all these values,
P 1 V 1 γ = P 2 V 2 γ
⇒ P 2 = 3 0 9 7 1 7 . 0 5 6 3 P a
Now,
The area on which this final pressure acts is,
A = 0 . 2 × 0 . 5 2 − 0 . 4 5 2 = 0 . 0 8 7 1 7 7 9 m 2
Thus,
F = P 2 A = 2 7 0 0 0 . 5 0 3 6 2 N
Since there are 4 tires,
F n e t = 4 F = 1 0 8 0 0 2 . 0 1 4 5 N
Hence,
M t o t a l = g F = 1 1 0 2 0 . 6 1 3 ≈ 1 1 0 2 1 K g