This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
u have to just find the indefinite integral which are just a few addition's and mul. consider
2x(1-x)
= -0.25 ( -8x(1-x) )
= -0.25 ( -2+2-8x(1-x) )
= -0.25 ( -2+2(1-4x(1-x) ) )
Thus
2x(1-x) e^2x(1-x)
=e^2x(1-x) [-0.25 ( -2+2(1-4x(1-x) ) )]
=-0.25 e^2x(1-x) [ -2+2(1-4x(1-x) ) ]
=using product rule
=-0.25 d/dx { (1-2x) e^2x(1-x) }
just integrate and get
I = -0.25 * (1-2x)e^2x(1-x)
Log in to reply
u mean this
2 x ( 1 − x )
= − 0 . 2 5 ( − 8 x ( 1 − x ) )
= − 0 . 2 5 ( − 2 + 2 − 8 x ( 1 − x ) )
= − 0 . 2 5 ( − 2 + 2 ( 1 − 4 x ( 1 − x ) ) ) Thus
2 x ( 1 − x ) e 2 x ( 1 − x )
= e 2 x ( 1 − x ) [ − 0 . 2 5 ( − 2 + 2 ( 1 − 4 x ( 1 − x ) ) ) ]
= − 0 . 2 5 e 2 x ( 1 − x ) [ − 2 + 2 ( 1 − 4 x ( 1 − x ) ) ] =using product rule
= − 0 . 2 5 d x d ( 1 − 2 x ) e 2 x ( 1 − x )
just integrate and get
I = − 0 . 2 5 ∗ ( 1 − 2 x ) e 2 x ( 1 − x )
I used a series to approximate the answer as 3 1 + 3 ⋅ 5 1 + 3 ⋅ 5 ⋅ 7 1 + . . . , which I'm not even sure is correct; I could've made a mistake. But, obviously, your way is better. I would have written it like this, however: 2 x ( 1 − x ) e 2 x ( 1 − x ) = − 0 . 2 5 ( 2 ( 4 x ( x − 1 ) e 2 x ( 1 − x ) ) ) = − 0 . 2 5 ( 2 ( 4 x 2 − 4 x ) e 2 x ( 1 − x ) ) = − 0 . 2 5 ( 2 ( ( 2 x − 1 ) 2 − 1 ) e 2 x ( 1 − x ) ) = − 0 . 2 5 ( 2 ( 1 − 2 x ) 2 e 2 x ( 1 − x ) − 2 e 2 x ( 1 − x ) ) = − 0 . 2 5 ( ( 1 − 2 x ) d ( 2 x ( 1 − x ) ) d [ e 2 x ( 1 − x ) ] ( 2 − 4 x ) − 2 e 2 x ( 1 − x ) ) = − 0 . 2 5 ( ( 1 − 2 x ) d ( 2 x ( 1 − x ) ) d [ e 2 x ( 1 − x ) ] d x d ( 2 x ( 1 − x ) ) + d x d [ 1 − 2 x ] e 2 x ( 1 − x ) ) = − 0 . 2 5 ( ( 1 − 2 x ) d x d [ e 2 x ( 1 − x ) ] + d x d [ 1 − 2 x ] e 2 x ( 1 − x ) ) = − 0 . 2 5 d x d [ ( 1 − 2 x ) e 2 x ( 1 − x ) ]
Set 2 x ( 1 − x ) e 2 x ( 1 − x ) = d x d [ ( a + b x ) e 2 x ( 1 − x ) ]
= b e 2 x ( 1 − x ) + ( a + b x ) e 2 x ( 1 − x ) ( 2 − 4 x )
= ( 2 a + b + ( − 4 a + 2 b ) x − 4 b x 2 ) e 2 x ( 1 − x ) .
Equating coefficients results in
2 a + b = 0
− 4 a + 2 b = 2
− 4 b = − 2
There is a unique solution to these equations, namely, ( a , b ) = ( − 4 1 , 2 1 ) .
Thus, ∫ 2 x ( 1 − x ) e 2 x ( 1 − x ) d x = ( − 4 1 + 2 1 x ) e 2 x ( 1 − x ) + C .
( − 4 1 + 2 1 x ) e 2 x ( 1 − x ) ∣ ∣ ∣ 0 1 = ( − 4 1 + 2 1 ) e 0 − ( − 4 1 ) e 0 = 2 1 .
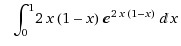
incredible mind Do post a solution for this, frankly typing XD i used wolfram alpha.