Definite integral: Practice
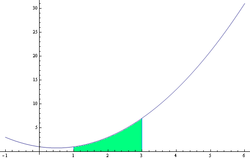 Let
f
(
x
)
=
x
2
−
x
+
1
, find the value of the following definite integral:
∫
1
3
f
(
x
)
d
x
Let
f
(
x
)
=
x
2
−
x
+
1
, find the value of the following definite integral:
∫
1
3
f
(
x
)
d
x
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Your solution is entirely unnecessary, you can just use the power rule of antiderivatives...
Log in to reply
Yup, using Riemann sums is a confirmation of that result.
put f(x)=xsquare-x+1 and solve
Use the power rule for antiderivatives. You get: ( 3 x 3 − 2 x 2 + x ) ∣ ∣ ∣ ∣ 1 3
= 6 5 4 − 6 2 7 + 6 1 8 − 6 2 + 6 3 − 6 6
= 6 4 0 = 3 2 0
We can use Riemann sums here, its definition is: ∫ a b f ( x ) d x = n → ∞ lim i = 1 ∑ n f ( x i ∗ ) Δ x where Δ x = n b − a and x i ∗ = a + ( Δ x ) i . For our problem, we recognize that: Δ x = n 3 − 1 = n 2 and so: x i ∗ = 1 + n 2 i , therefore: f ( x i ∗ ) = ( 1 + n 2 i ) 2 − ( 1 + n 2 i ) + 1 = 1 + n 4 i + n 2 4 i 2 − 1 − n 2 i + 1 = 1 + n 2 i + n 2 4 i 2 . So by definition: ∫ 1 3 ( x 2 − x + 1 ) d x = n → ∞ lim i = 1 ∑ n f ( x i ∗ ) Δ x = n → ∞ lim i = 1 ∑ n [ 1 + n 2 i + n 2 4 i 2 ] n 2 = n → ∞ lim [ i = 1 ∑ n 1 + i = 1 ∑ n n 2 i + i = 1 ∑ n n 2 4 i 2 ] n 2 = n → ∞ lim [ i = 1 ∑ n 1 + n 2 i = 1 ∑ n i + n 2 4 i = 1 ∑ n i 2 ] n 2 = ( ⋆ ) n → ∞ lim [ n + n 2 2 n ( n + 1 ) + n 2 4 6 n ( n + 1 ) ( 2 n + 1 ) ] n 2 = n → ∞ lim [ 2 + n 2 4 2 n ( n + 1 ) + n 3 8 6 n ( n + 1 ) ( 2 n + 1 ) ] = n → ∞ lim [ 2 + 2 n 2 n 2 + n + 3 4 n 3 2 n 3 + O ( n ) ] = 2 + 2 + 3 4 ⋅ 2 = 4 + 3 8 = 3 2 0 .