Definite integral red area

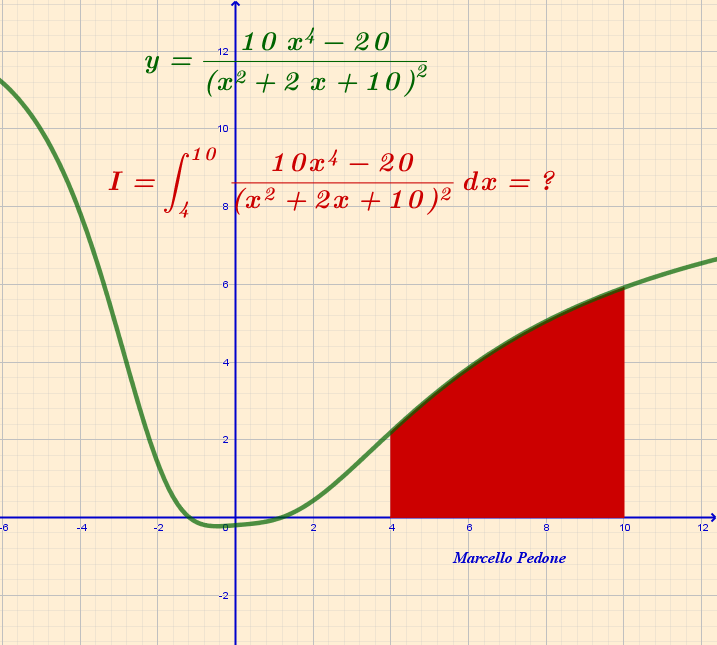
By using Polynomial long division and Partial fraction decomposition you get

$\begin{aligned} y&=10\frac{x^4-2}{(x^2+2x+10)^2}=10\frac{p(x)}{q(x)}\\ &=10\left(1-\underbrace{\frac{4x^3+24x^2+40x+102}{q(x)}}_{r(x)}\right)\\ r(x)&=\frac{bx+c}{\sqrt{q}}+\frac{dx+f}{q}\\ b&=4\\ c&=16\\ d&=-32\\ f&=-58 \end{aligned}$ .

$\\ ~\\$

And with the help of https://de.wikipedia.org/wiki/Partialbruchzerlegung /6.2 (I only found it in german) you can find a Antiderivative:

$\begin{aligned} \int y\,\mathrm dx&=10\left(x-\int r\,\mathrm{d}x\right)\\ \int r\,\mathrm dx&=2\ln(\sqrt{q})+\frac{95}{27}\arctan\left(\frac{x+1}{3}\right)+\frac{144-13(x+1)}{9}\cdot\frac{1}{\sqrt{q}} \end{aligned}$

$\\$

And so:

$I \approx 26,1 ~~~~~~~\Rightarrow \boxed{26<I<27}$