Delta Winding - Common Mode Removal

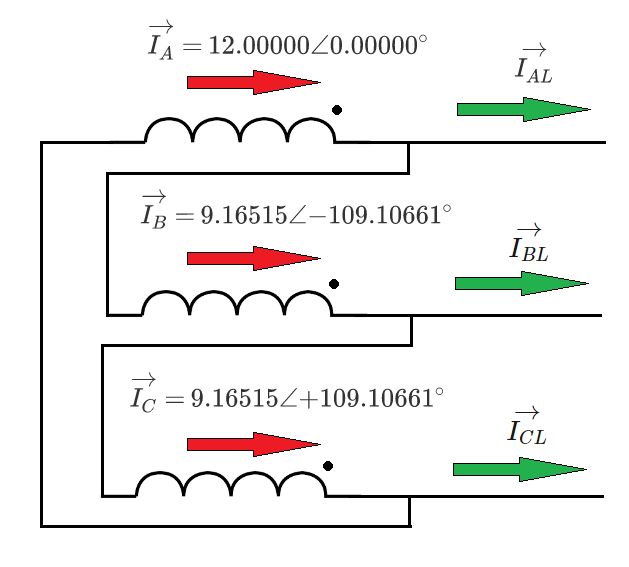
A set of three-phase AC (alternating current) transformer windings is connected in a delta configuration, as shown above. Other windings are not shown. Winding currents $(\vec{I_A},\vec{I_B}, \vec{I_C})$ and line currents $(\vec{I_{AL}},\vec{I_{BL}}, \vec{I_{CL}})$ are also pictured.

The following relationship holds for these currents (to a close numerical approximation):

$\large{\vec{I_{AL}} = \vec{\alpha} (\vec{I_A} - \vec{\beta}) \\ \vec{I_{BL}} = \vec{\alpha} (\vec{I_B} - \vec{\beta}) \\ \vec{I_{CL}} = \vec{\alpha} (\vec{I_C} - \vec{\beta})}$

To one decimal place, what is the magnitude (absolute value) of $(\vec{\alpha} + \vec{\beta})$ ?

Notes:

• $\vec{\alpha}$ and $\vec{\beta}$ are complex numbers .

• In general, $A \angle \theta$ denotes a complex number with a magnitude of $A$ and an angle $\theta$ with respect to the positive real axis

• Angles are given in degrees

• Vector multiplication here is NOT the dot product. For example: $(A + jB)(C + jD) = AC - BD + j(AD + BC)$ .

• Feel free to use a calculator to do the complex arithmetic.