Density through Stress-distance graph!
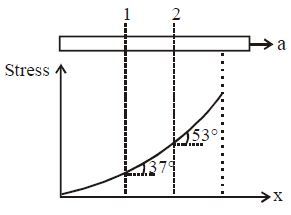 Rod of constant cross-section moves towards right with constant acceleration. Graph of
stress and distance from left end is given as in figure. If density of material of rod at cross
section
1
is
9
c
m
3
g
. Find density at cross section
2
in
c
m
3
g
.
Rod of constant cross-section moves towards right with constant acceleration. Graph of
stress and distance from left end is given as in figure. If density of material of rod at cross
section
1
is
9
c
m
3
g
. Find density at cross section
2
in
c
m
3
g
.
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
There is a typo in the question it should be 9 g/cm^3
Log in to reply
i made a mistake while writing ρ 1 . Now i have edited the problem. ρ 1 = 9 c m 3 g
Kyle Finch
I came to the same solution (except there is a typo as Kyle said) but what I don't understand is why would the density increase with x? My intuition tells me the density should decrease with x, and the slope should be decreasing with x.
Can you please explain why the density increases with +x instead of decreases?
Log in to reply
Yes it is more intuitive to imagine mass accumulating to resist motion and hence more mass concentrated at the tip (x=0). This would mean higher density near x=0. But this is a rigid body and cannot deform and application of Newton's laws gives higher density at x=L.
I agree with you , I think density should be max at x = 0.