Fun of Derangement 1

Probability Level 1

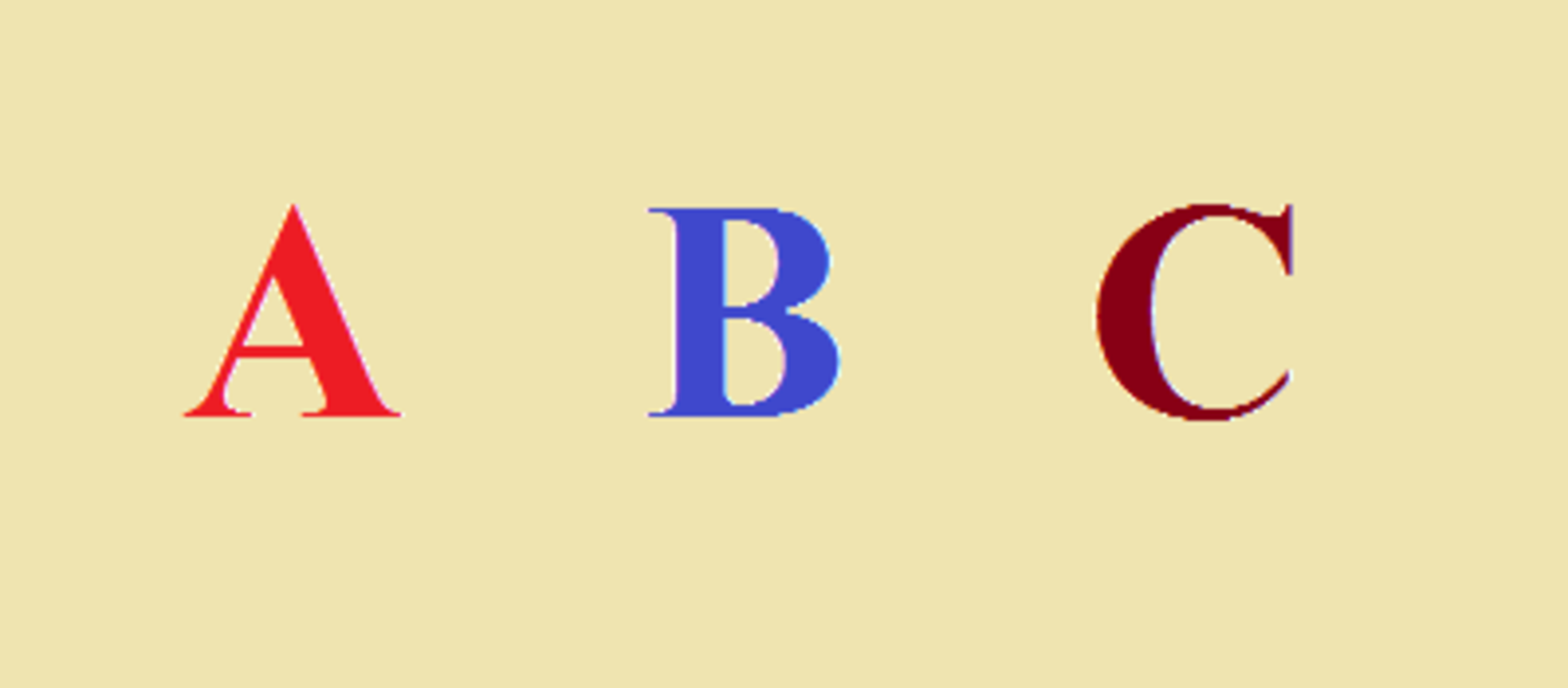How many ways is there that we can arrange A,B,C as if they do not position themselves ?

Note that:

CAB is a possible arrange because they didn't position themselves.
ACB is not a possible arrange because, A didn't follow the rules.

1 6 4 2

2 solutions

Tushar Showrav
Sep 8, 2016

From the derangement theorem we can write , => !3 = $\frac{3!}{2!}$ - $\frac{3!}{3!}$ => !3 = 3 - 1 => !3 = 2 So, the Answer is: 2

Note that:

!3 means , derangement of 3

Jingyang Tan
Nov 29, 2016

In position $A$ , we can put $B,C$
In Position $B$ ,we can put $C,A$
In Position $C$ , we can put $A,B$
We then find how many Combinations are there.
Combination 1: $B,C,A$
Combination 2: $C,A,B$
In the end,There are 2 combinations.