Descartes Sangaku : The Beast part 1

Geometry Level pending
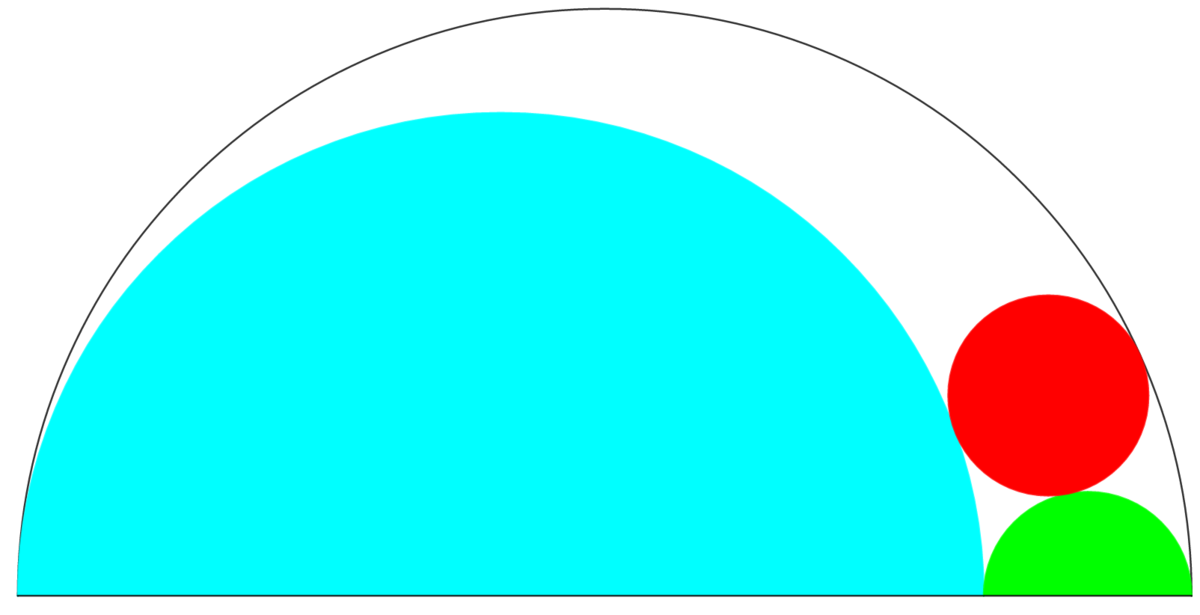
  • The diagram shows a semi-circle of radius 1. We place a point on its diameter.
  • This point allows us to draw two semi-circles (green and cyan).
  • We inscribe a red circle so that this circle is tangent to the other three semi-circles.
  • The center of the semi-circle of radius 1 is the origin of the coordinate system.

The question: What is the area of the red circle when the sum of the coordinates of its center is maximum? The answer can be expressed as a − b ⋅ c d ⋅ π \boxed{\frac{a-b\cdot \sqrt{c}}{d}\cdot \pi } where a a , b b , c c , d d are positive integers. Evaluate d − a − b − c \boxed{\sqrt{d-a-b-c}}


The answer is 5.

Valentin Duringer by Valentin Duringer , 30, Belgium

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Valentin Duringer
Aug 18, 2020
  • To solve this problem, we shall denote the radius of the cyan semi-circle as x \boxed{x} , the radius of the green semi-circle as 1 − x \boxed{1-x} and the radius of the blue circle as R ( x ) \boxed{R(x)} , l ( x ) \boxed{l(x)} is the x x coordinate of the red circle's center and h ( x ) \boxed{h(x)} is the y y coordinate of the red circle's center.

  • We shall use the Pythagorean theorem to express R ( x ) \boxed{R(x)} , l ( x ) \boxed{l(x)} and h ( x ) \boxed{h(x)} in terms of x \boxed{x}

  • We shall write three equations using the diagram:

  • ( 1 − R ( x ) ) 2 = l ( x ) 2 + h ( x ) 2 \boxed{(1-R(x))^{2}=l(x)^{2}+h(x)^{2}}
  • ( 1 − x + R ( x ) ) 2 = ( x − l ( x ) ) 2 + h ( x ) 2 \boxed{(1-x+R(x))^{2}=(x-l(x))^{2}+h(x)^{2}}
  • ( x + R ( x ) ) 2 = ( 1 − x + l ( x ) ) 2 + h ( x ) 2 \boxed{(x+R(x))^{2}=(1-x+l(x))^{2}+h(x)^{2}}
  • After combining the equation and using minor algebra skills we find:
  • R ( x ) = x − x 2 x 2 − x + 1 \boxed{R(x)=\frac{x-x^{2}}{x^{2}-x+1}}
  • l ( x ) = 2 x − 1 x 2 − x + 1 \boxed{l\left(x\right)=\frac{2x-1}{x^2-x+1}}
  • h ( x ) = 2 ⋅ ( x 2 − x ) − x 2 + x − 1 \boxed{h\left(x\right)=2\cdot \frac{\left(x^2-x\right)}{-x^2+x-1}}
  • Then the function S ( x ) = 2 ⋅ ( x 2 − x ) − x 2 + x − 1 + 2 x − 1 x 2 − x + 1 \boxed{S(x)=2\cdot \frac{\left(x^2-x\right)}{-x^2+x-1}+\frac{2x-1}{x^2-x+1}} is the sum of the coordinates.
  • S ′ ( x ) = ( 3 − 2 x − 2 x 2 ) ( − 1 + x − x 2 ) 2 \boxed{S'(x)=\frac{\left(3\:-\:2\:x\:-\:2\:x^2\right)}{\left(-1\:+\:x\:-\:x^2\right)^2}}
  • After solving S ′ ( x ) = 0 \boxed{S'(x)=0} we find x = 7 − 1 2 \boxed{x=\frac{\sqrt{7}-1}{\:2}}
  • We calculate the area of the red circle for x = 7 − 1 2 \boxed{x=\frac{\sqrt{7}-1}{\:2}} : π ⋅ R ( x ) 2 = π ⋅ 23 − 8 7 63 \boxed{\pi \cdot R(x)^{2}=\pi \cdot \frac{23-8\sqrt{7}}{63}}
  • d − a − b − c = 5 \boxed{\sqrt{d-a-b-c=5}}
0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...