Descartes Sangaku : The End part 1

Geometry Level pending
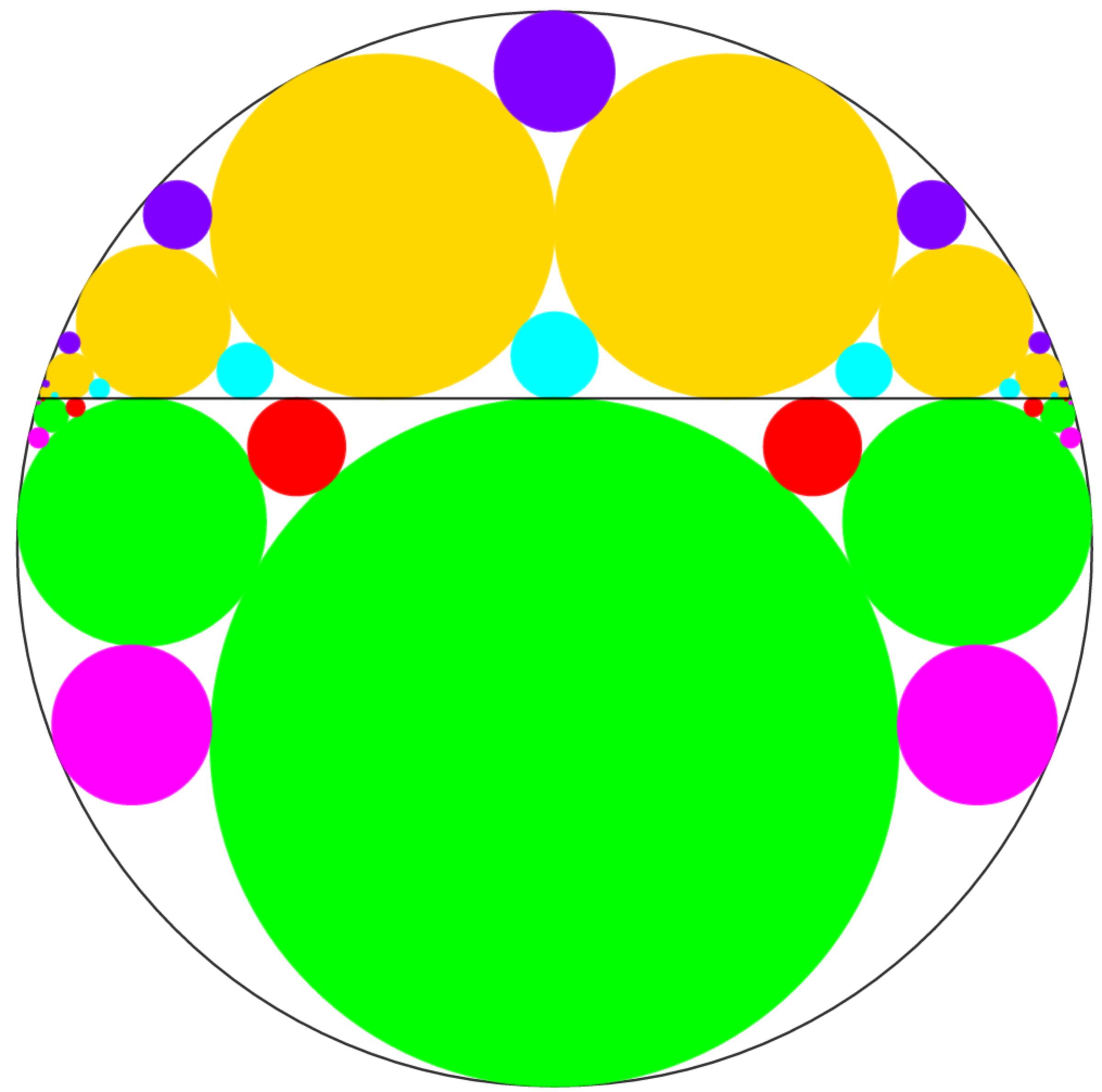
  • The diagram shows a black circle of radius 25 \boxed{25} .
  • We drawn an horizontal black line to divide this circle into two circular segments. This line a length 48 \boxed{48} .
  • Now we pack the top circulair segment with 3 types of circles : Y e l l o w \color{#CEBB00}Yellow , C y a n \color{cyan}Cyan and P u r p l e \color{#69047E}Purple .
  • Then we pack the bottom circular segment with 3 types of circles : G r e e n \color{#20A900}Green , R e d \color{#D61F06}Red and P i n k \color{#E81990}Pink
  • Note : The two biggest yellow circles are congruent.
  • The bottom circular segment is larger than the top circular segment
  • We count the circles starting from the largest of its sequence to the right (or left) towards the infinitely small circles
  • We focus on the Y e l l o w \color{#CEBB00}Yellow and G r e e n \color{#20A900}Green circles in this problem. The largest G r e e n \color{#20A900}Green circle is the 0 t h 0^{th} circle of its sequence. The largest Y e l l o w \color{#CEBB00}Yellow circle is the 0 t h 0^{th} circle of its sequence.

The question: The radius of the n t h n^{th} Y e l l o w \color{#CEBB00}Yellow circle (for n ≥ 0 n≥0 ) can be expressed as ( a + b ) b ⋅ b ( b ⋅ n + a + b ) ( b b ⋅ n + a + a ) b \boxed{\frac{\left(a+b\right)^b\cdot b^{\left(b\cdot \:n+a+b\right)}}{\left(b^{b\cdot n+a}+a\right)^b}} and the radius of the n t h n^{th} G r e e n \color{#20A900}Green circle (for n ≥ 0 n≥0 ) can be expressed as c d ⋅ d ( n ⋅ c ) ( d ( n ⋅ c ) + c − d ) c \boxed{\frac{c^d\cdot d^{\left(^{n\cdot \:\sqrt{c}}\right)}}{\left(d^{\left(^{n\cdot \:\sqrt{c}}\right)}+c-d\right)^{\sqrt{c}}}} where a a , b b , c c , d d are positive integers. Calculate a + b + c + d \boxed{a+b+c+d}


The answer is 10.

Valentin Duringer by Valentin Duringer , 30, Belgium

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Valentin Duringer
Aug 20, 2020
  • First we need to know the heights of both circular segments. We use the product of chords theorem in a circle :
  • ( 48 2 ) 2 = h 1 ⋅ h 2 \boxed{\left(\frac{48}{2}\right)^2=h_1\cdot \:h_2} < = > <=> h 1 = 18 \boxed{h_1=18} and h 2 = 32 \boxed{h_2=32} since h 1 = 50 − h 2 \boxed{h_1=50-h_2}
  • Then the largest green circle has radius 32 2 = 16 \boxed{\frac{32}{2}=16}
  • To calculate the radii of consecutive green circles we use the pythagorean theorem:
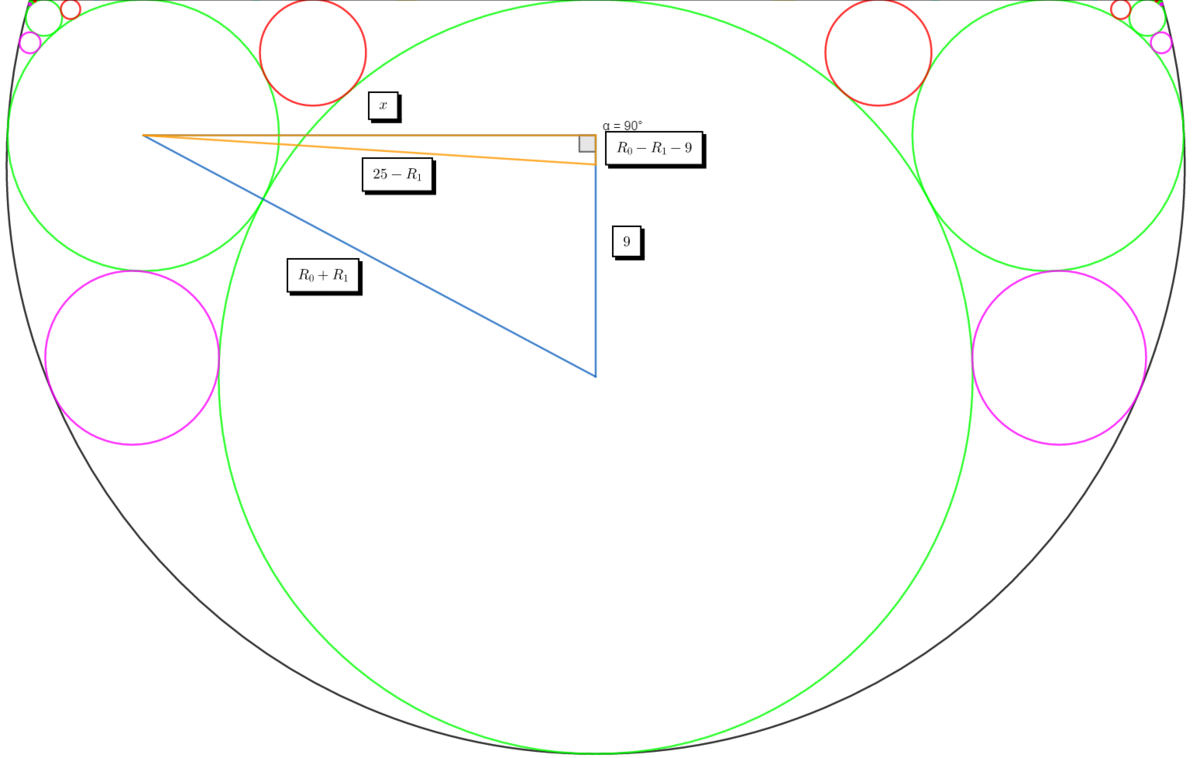
  • We use those two right triangles to write two equations: { ( R 0 + R 1 ) 2 = ( R 0 − R 1 ) 2 + x 2 ( 25 − R 1 ) 2 = ( R 0 − R 1 − 9 ) 2 + x 2 \begin{cases}\left(R_0+R_1\right)^2=\left(R_0-R_1\right)^2+x^2\\\left(25-R_1\right)^2=\left(R_0-R_1-9\right)^2+x^2\end{cases}
  • R 0 = 16 \boxed{R_0=16} and 9 \boxed{9} is the distance bewteen the center of the largest circle containing all the others and the center of the green circle.
  • After solving the system of equations we find R 1 = \color{#20A900}R_1= 144 25 \boxed{\frac{144}{25}}
  • We can repeat this process to find the first 5 terms of the sequence:
  • R 0 = \color{#20A900}R_0= 16 1 \boxed{\frac{16}{1}}
  • R 1 = \color{#20A900}R_1= 144 25 \boxed{\frac{144}{25}}
  • R 2 = \color{#20A900}R_2= 1296 1681 \boxed{\frac{1296}{1681}}
  • R 3 = \color{#20A900}R_3= 11664 133225 \boxed{\frac{11664}{133225}}
  • R 4 = \color{#20A900}R_4= 104976 10764961 \boxed{\frac{104976}{10764961}}
  • Let's look at the numerator. It's difficult to identify a pattern, but with some effort and research, we can rewrite them :
  • 16 = ( 4 ) 2 = ( 4 ⋅ 3 0 ) 2 \boxed{16=\left(4\right)^2=\left(4\cdot 3^0\right)^2}
  • 144 = ( 12 ) 2 = ( 4 ⋅ 3 1 ) 2 \boxed{144=\left(12\right)^2=\left(4\cdot 3^1\right)^2}
  • 1296 = ( 36 ) 2 = ( 4 ⋅ 3 2 ) 2 \boxed{1296=\left(36\right)^2=\left(4\cdot 3^2\right)^2}
  • 11664 = ( 108 ) 2 = ( 4 ⋅ 3 3 ) 2 \boxed{11664=\left(108\right)^2=\left(4\cdot 3^3\right)^2}
  • 104976 = ( 324 ) 2 = ( 4 ⋅ 3 4 ) 2 \boxed{104976=\left(324\right)^2=\left(4\cdot 3^4\right)^2}
  • The numerator can be written as ( 4 ⋅ 3 n ) 2 \boxed{\left(4\cdot 3^n\right)^2}
  • Let's look at the denominator. It's difficult to identify a pattern, but with some effort and research, we can rewrite them :
  • 1 = 4 4 = 2 2 4 = ( 3 2 ⋅ 0 + 1 ) 2 4 \boxed{1=\frac{4}{4}=\frac{2^2}{4}=\frac{\left(3^{2\cdot 0}+1\right)^2}{4}}
  • 25 = 100 4 = 1 0 2 4 = ( 3 2 ⋅ 1 + 1 ) 2 4 \boxed{25=\frac{100}{4}=\frac{10^2}{4}=\frac{\left(3^{2\cdot 1}+1\right)^2}{4}}
  • 1681 = 6724 4 = 8 2 2 4 = ( 3 2 ⋅ 2 + 1 ) 2 4 \boxed{1681=\frac{6724}{4}=\frac{82^2}{4}=\frac{\left(3^{2\cdot 2}+1\right)^2}{4}}
  • 133225 = 532900 4 = 73 0 2 4 = ( 3 2 ⋅ 3 + 1 ) 2 4 \boxed{133225=\frac{532900}{4}=\frac{730^2}{4}=\frac{\left(3^{2\cdot 3}+1\right)^2}{4}}
  • 10764961 = 43059844 4 = 656 2 2 4 = ( 3 2 ⋅ 4 + 1 ) 2 4 \boxed{10764961=\frac{43059844}{4}=\frac{6562^2}{4}=\frac{\left(3^{2\cdot 4}+1\right)^2}{4}}
  • The denominator can be written as ( 3 2 ⋅ n + 1 ) 2 4 \boxed{\frac{\left(3^{2\cdot n}+1\right)^2}{4}}
  • Then R n = \color{#20A900}R_n= 64 ⋅ 3 2 ⋅ n ( 3 2 ⋅ n + 1 ) 2 = 4 3 ⋅ 3 n ⋅ 4 ( 3 n ⋅ 4 + 4 − 3 ) 4 \boxed{\frac{64\cdot \:\:3^{2\cdot n}}{\left(3^{2\cdot \:n}+1\right)^2}=\frac{4^3\cdot \:\:\:3^{n\cdot \sqrt{4}}}{\left(3^{n\cdot \sqrt{4}}+4-3\right)^{\sqrt{4}}}}
  • Then c = 4 \boxed{c=4} and d = 3 \boxed{d=3}
  • We can use a similar method to get the radii of the yellow circles, the consecutive Pythagorean equations give the sequence:
  • R 0 = \color{#CEBB00}R_0= 8 1 \boxed{\frac{8}{1}}
  • R 1 = \color{#CEBB00}R_1= 32 9 \boxed{\frac{32}{9}}
  • R 2 = \color{#CEBB00}R_2= 128 121 \boxed{\frac{128}{121}}
  • R 3 = \color{#CEBB00}R_3= 512 1849 \boxed{\frac{512}{1849}}
  • R 4 = \color{#CEBB00}R_4= 2048 29241 \boxed{\frac{2048}{29241}}
  • Let's look at the numerator. We can rewrite them :
  • 8 = 2 2 ⋅ 0 + 3 \boxed{8=2^{2\cdot 0+3}}
  • 32 = 2 2 ⋅ 1 + 3 \boxed{32=2^{2\cdot 1+3}}
  • 128 = 2 2 ⋅ 2 + 3 \boxed{128=2^{2\cdot 2+3}}
  • 512 = 2 2 ⋅ 3 + 3 \boxed{512=2^{2\cdot 3+3}}
  • 2048 = 2 2 ⋅ 4 + 3 \boxed{2048=2^{2\cdot 4+3}}
  • The numerator can be written as 2 2 ⋅ n + 3 \boxed{2^{2\cdot n+3}}
  • Let's look at the denominator. It's difficult to identify a pattern, but with some effort and research, we can rewrite them :
  • 1 = 1 2 = ( 3 3 ) 2 = ( 2 2 ⋅ 0 + 1 + 1 3 ) 2 \boxed{1=1^2=\left(\frac{3}{3}\right)^2=\left(\frac{2^{2\cdot 0+1}+1}{3}\right)^2}
  • 9 = 3 2 = ( 9 3 ) 2 = ( 2 2 ⋅ 1 + 1 + 1 3 ) 2 \boxed{9=3^2=\left(\frac{9}{3}\right)^2=\left(\frac{2^{2\cdot 1+1}+1}{3}\right)^2}
  • 121 = 1 1 2 = ( 33 3 ) 2 = ( 2 2 ⋅ 2 + 1 + 1 3 ) 2 \boxed{121=11^2=\left(\frac{33}{3}\right)^2=\left(\frac{2^{2\cdot 2+1}+1}{3}\right)^2}
  • 1849 = 4 3 2 = ( 129 3 ) 2 = ( 2 2 ⋅ 3 + 1 + 1 3 ) 2 \boxed{1849=43^2=\left(\frac{129}{3}\right)^2=\left(\frac{2^{2\cdot 3+1}+1}{3}\right)^2}
  • 29241 = 17 1 2 = ( 513 3 ) 2 = ( 2 2 ⋅ 4 + 1 + 1 3 ) 2 \boxed{29241=171^2=\left(\frac{513}{3}\right)^2=\left(\frac{2^{2\cdot 4+1}+1}{3}\right)^2}
  • We can then write the denominator as ( 2 2 n + 1 + 1 3 ) 2 \boxed{\left(\frac{2^{2n+1}+1}{3}\right)^2}
  • Then R n = \color{#CEBB00}R_n= 9 ⋅ 2 2 n + 3 ( 2 2 n + 1 + 1 ) 2 = ( 1 + 2 ) 2 ⋅ 2 2 n + 1 + 2 ( 2 2 n + 1 + 1 ) 2 \boxed{\frac{9\cdot \:\:\:2^{2n+3}}{\left(2^{2n+1}+1\right)^2}=\frac{\left(1+2\right)^2\cdot \:2^{2n+1+2}}{\left(2^{2n+1}+1\right)^2}}
  • Then a = 1 \boxed{a=1} and b = 2 \boxed{b=2}
  • Finally a + b + c + d = 1 + 2 + 3 + 4 = 10 \boxed{a+b+c+d=1+2+3+4=10}
1 Helpful 1 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...