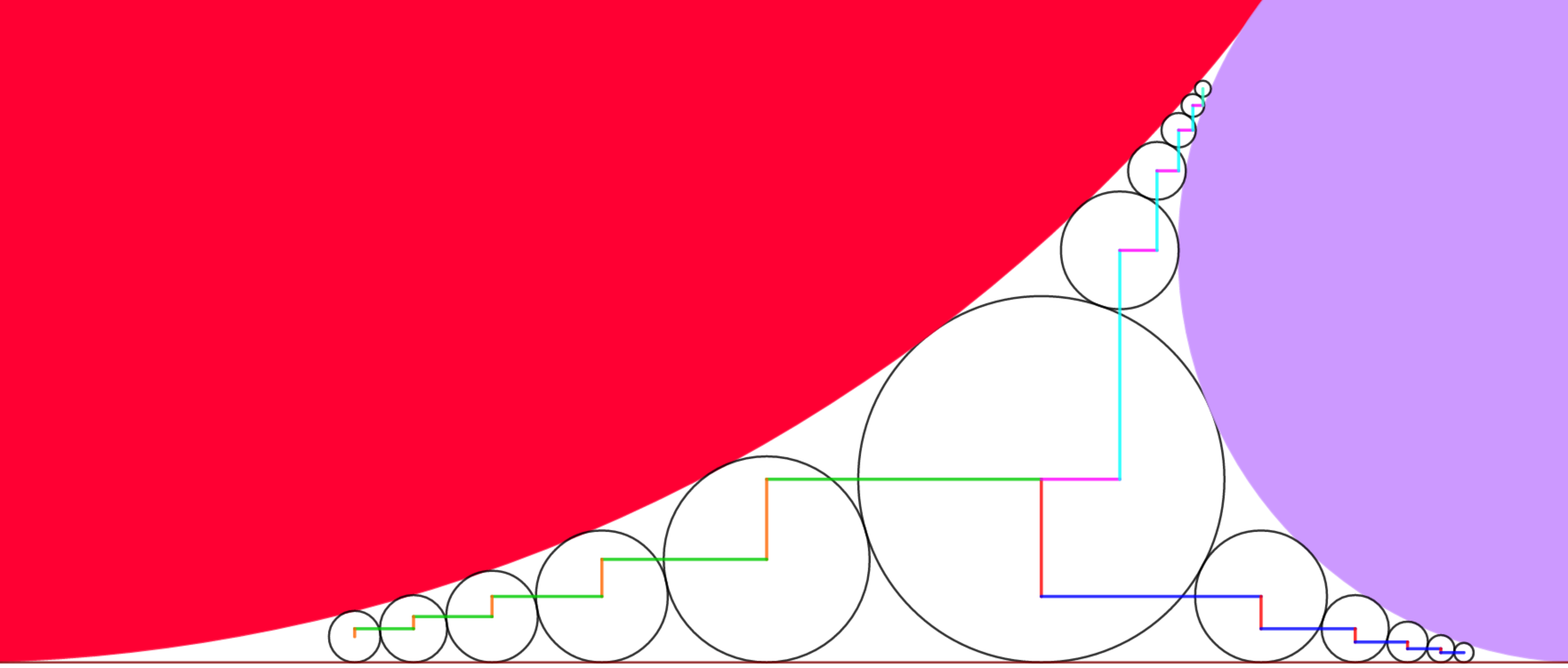
Descartes Sangaku :The stairway part 3

Geometry Level pending

The diagram shows a red circle with radius $\boxed{\frac{1}{2}}$ and a purple circle with radius $\boxed{\frac{1}{8}}$ tangent to each other and mutually tangent to the same brown line
We inscribe a circle between the brown line, the red circle and the purple circle.
Then we pack the space with circles to the left, to the right and to the top.
At last we build 3 stairways by connecting the center of consecutive circles ; consecutive stairs are perpendicular to each other.

We consider the stairway built to the top of the diagram. This stairway is composed of cyan vertical lines and pink horizontal lines.
The $n^{th}$ cyan vertical line is denoted as $\boxed{\color{cyan}V_n}$ .
The $n^{th}$ pink horizontal line is denoted as $\boxed{\color{#E81990}H_n}$ .

The question: Evaluate : $\boxed{\frac{\sum _{n=50}^{60}\:\color{cyan}V_n}{\sum _{n=50}^{60}\:\color{#E81990}H_n}}$ , for $n≥1$ the answer can be expressed as $\boxed{\frac{a}{b}}$ where $a$ and $b$ are coprime positive integers. Calculate $\boxed{a-b}$

The answer is 6659.

2 solutions

Fletcher Mattox
Aug 23, 2020

It took me a while to find the polynomials, but I eventually found the same ones you did.

from sympy import *
I = Integer

def f(n):
    r = I(1)/(10*n**2 + 8*n)
    x = (9*n + I(6)) / (10*n + 8)
    y = (2*n**2 - I(1)) / (10*n**2 + 8*n)
    return r, x, y

print("first few circles ...")
for n in range(1, 10):
    r, x, y = f(n)
    print("%r, (%r, %r)" % (r, x, y))

r0, x0, y0 = f(50)
r1, x1, y1 = f(61)
delta_x = x1 - x0
delta_y = y1 - y0
print("\nsolution:")
soln = delta_y / delta_x
print(soln)
a, b = fraction(soln)
print("%r - %r = %r" % (a, b, a - b))

first few circles ...
1/18, (5/6, 1/18)
1/56, (6/7, 1/8)
1/114, (33/38, 17/114)
1/192, (7/8, 31/192)
1/290, (51/58, 49/290)
1/408, (15/17, 71/408)
1/546, (23/26, 97/546)
1/704, (39/44, 127/704)
1/882, (87/98, 23/126)

solution:
24959/18300
24959 - 18300 = 6659

I'm happy someone tries (with success) to solve my problems! Interesting that you use python...

Valentin Duringer - 9 months, 3 weeks ago

I am fascinated by interesting circle tangencies. So I am attracted to your problems. Most of them are too hard for me. I'm not a mathematician. I'm just a retired hacker. That explains the python. I annoy folks by posting code. When your only tool is a hammer everything looks like a nail. :)

Fletcher Mattox - 9 months, 3 weeks ago

I posted my last problems, let's see if you can hack those...

Valentin Duringer - 9 months, 3 weeks ago

At the moment I am stuck on "The End pt 1". So I may switch to "My Ultimate", as it looks more tractable. Actually you have shared so many interesting Sangakus, I could stay busy for a lifetime.

Question: Descartes's theorem is typically applied to three externally tangent circles. Is it also useful for two external and one internal tangency? For example, by simply changing the sign on one of the curvatures? Or should I be constructing similar triangles? Thank you.

Fletcher Mattox - 9 months, 3 weeks ago

My researches lead me to explore different kinds of progression about circle's radii when there is tangency (the point for me being that the radii needs to be rational !). And as you've seen by now, the progression can be written as a polynomial formula (2nd degree) almost always, but actually, when the progression happens in a circular segment, it's not a polynomial, it's about power function ! And some of the sequences in "the end" can not even be found here http://oeis.org/ ! About circles internally tangent : http://www.gogeometry.com/geometry/soddy descartes circles.htm But this link won't help you for "the end", well, it will help only if i make a part 3. Or it will help for "the aberration". This website has many, many interesting problems, if you need inspiration go there, there is amazing material. About triangles, it will help (right triangle will surely). Are they similar? I dont think so...? See you in the end !

Valentin Duringer - 9 months, 3 weeks ago

Valentin Duringer
Aug 19, 2020

First, let's calculate the sequence of radii of consecutive circles going to the top, starting from the central black circle. Using Descartes Circle's Theorem, we get the 6 first radii of the sequence:
$\boxed{\frac{1}{18}}$
$\boxed{\frac{1}{56}}$
$\boxed{\frac{1}{114}}$
$\boxed{\frac{1}{192}}$
$\boxed{\frac{1}{290}}$
$\boxed{\frac{1}{408}}$
We notice that the numerator stays the same, and we can substract the consecutive denominators and identify a pattern :
$\boxed{56-18=18+20\cdot 1}$
$\boxed{114-56=18+20\cdot 2}$
$\boxed{192-114=18+20\cdot 3}$
$\boxed{290-192=18+20\cdot 4}$
$\boxed{408-290=18+20\cdot 5}$
We can conclude : $\boxed{R_n=\frac{1}{10n^2+8n}}$

Now we can use a coordinate system to calculate the coordinates of the consecutive circle's center.
We give the central black circle the equation : $\boxed{x^2+\left(y-\frac{1}{18}\right)^2-\frac{1}{18^2}=0}$
We give the red circle the equation : $\boxed{\left(x+\frac{1}{3}\right)^2+\left(y-\frac{1}{2}\right)^2-\frac{1}{2^2}=0}$
We give the purple circle the equation : $\boxed{\left(x-\frac{1}{6}\right)^2+\left(y-\frac{1}{8}\right)^2-\frac{1}{8^2}=0}$
If $C_n(x_n;y_n)$ is the center of the $n^{th}$ circle we can find $x_n$ and $y_n$ but solving this system of equation:
$\begin{cases}\left(x_n-\frac{1}{6}\right)^2+\left(y_n-\frac{1}{8}\right)^2-\left(\frac{1}{8}+R_n\right)^2=0 \\\left(x_n+\frac{1}{3}\right)^2+\left(y_n-\frac{1}{2}\right)^2-\left(\frac{1}{2}+R_n\right)^2=0\end{cases}$
We find the following coordinates:
$\boxed{x_1=0}$ ; $\boxed{y_1=\frac{1}{18}}$
$\boxed{x_2=\frac{1}{42}}$ ; $\boxed{y_2=\frac{7}{56}}$
$\boxed{x_3=\frac{2}{57}}$ ; $\boxed{y_3=\frac{17}{114}}$
$\boxed{x_4=\frac{1}{24}}$ ; $\boxed{y_4=\frac{31}{192}}$
$\boxed{x_5=\frac{4}{87}}$ ; $\boxed{y_5=\frac{49}{290}}$
$\boxed{x_6=\frac{5}{102}}$ ; $\boxed{y_6=\frac{71}{408}}$
Let's look at the $y$ values. Each time the denominator is the radius of the concerned circle. By rewritting the consecutive numerators when identify a pattern:
$\boxed{1=1^2\cdot 2-1}$
$\boxed{7=2^2\cdot 2-1}$
$\boxed{17=3^2\cdot 2-1}$
$\boxed{31=4^2\cdot 2-1}$
$\boxed{49=5^2\cdot 2-1}$
$\boxed{71=6^2\cdot 2-1}$
We can conclude that $\boxed{y_n=\frac{2n^2-1}{10n^2+8n}}$
Obviously, the length of $\boxed{\color{cyan}V_n}$ is equal to $\boxed{y_{n+1}-y_n}$
Then $\color{cyan}V_n$ $V_{n}$ = $\boxed{\frac{2\left(n+1\right)^2-1}{10\left(n+1\right)^2+8\left(n+1\right)}-\frac{2n^2-1}{10n^2+8n}}$ $\frac{2 ( n + 1 ) ^{2} - 1}{1 0 ( n + 1 ) ^{2} + 8 ( n + 1 )} - \frac{2 n ^{2} - 1}{1 0 n ^{2} + 8 n}$
- Now, we notice that we can make a right triangle by using the center of two consecutive circles. Joining their center makes the hypothenuse, the cyan and pink lines are the legs of the triangle. This allows use to write this pythagorean equality:
$\boxed{\left(R_n+R_{n+1}\right)^2=\color{cyan}V_n^2+\color{#E81990}H_n^2}$
knowing the expression of $R_{n+1}$ , $R_n$ and $\color{cyan}V_n$ in terms of $n$ we get :
Then $\color{#E81990}H_n$ = $\boxed{\frac{3}{\left(5n+4\right)\left(5n+9\right)}}$

$\boxed{\frac{\sum _{n=50}^{60}\:\color{cyan}V_n}{\sum _{n=50}^{60}\:\color{#E81990}H_n}=\frac{24949}{18300}}$
$\boxed{a-b=24949-18300=6659}$

Descartes Sangaku :The stairway part 3

The answer is 6659.

2 solutions

0 pending reports