design of a hat
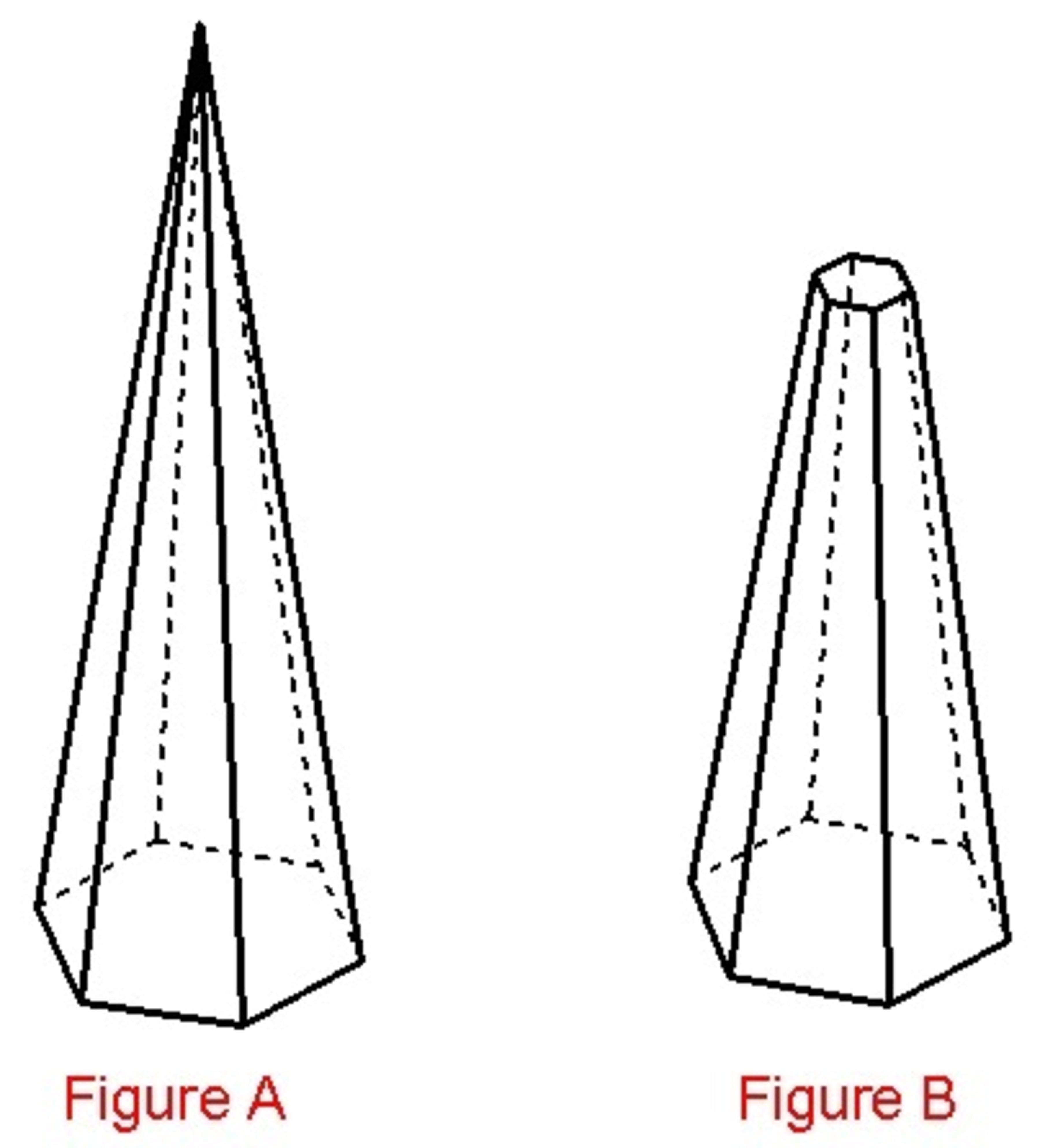
A little boy is going to a party tomorrow. He wants to have a weird hat. So, from a cardboard, he constructed a hat (figure ). The height is 60 cm and the base is in the shape of a regular hexagon with an edge length of 9 cm. He then cuts the upper portion of the hat by passing a perpendicular plane 42 cm from the base to have the final design (figure ). What is the surface area (in square centimeters) of the final design? Give your answer to the nearest integer.
Remarks:
- Figure A is in the shape of a regular pyramid.
- Don't include the area inside the hat.
The answer is 1487.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 2 x = 6 0 9 ⟹ x = 6 . 3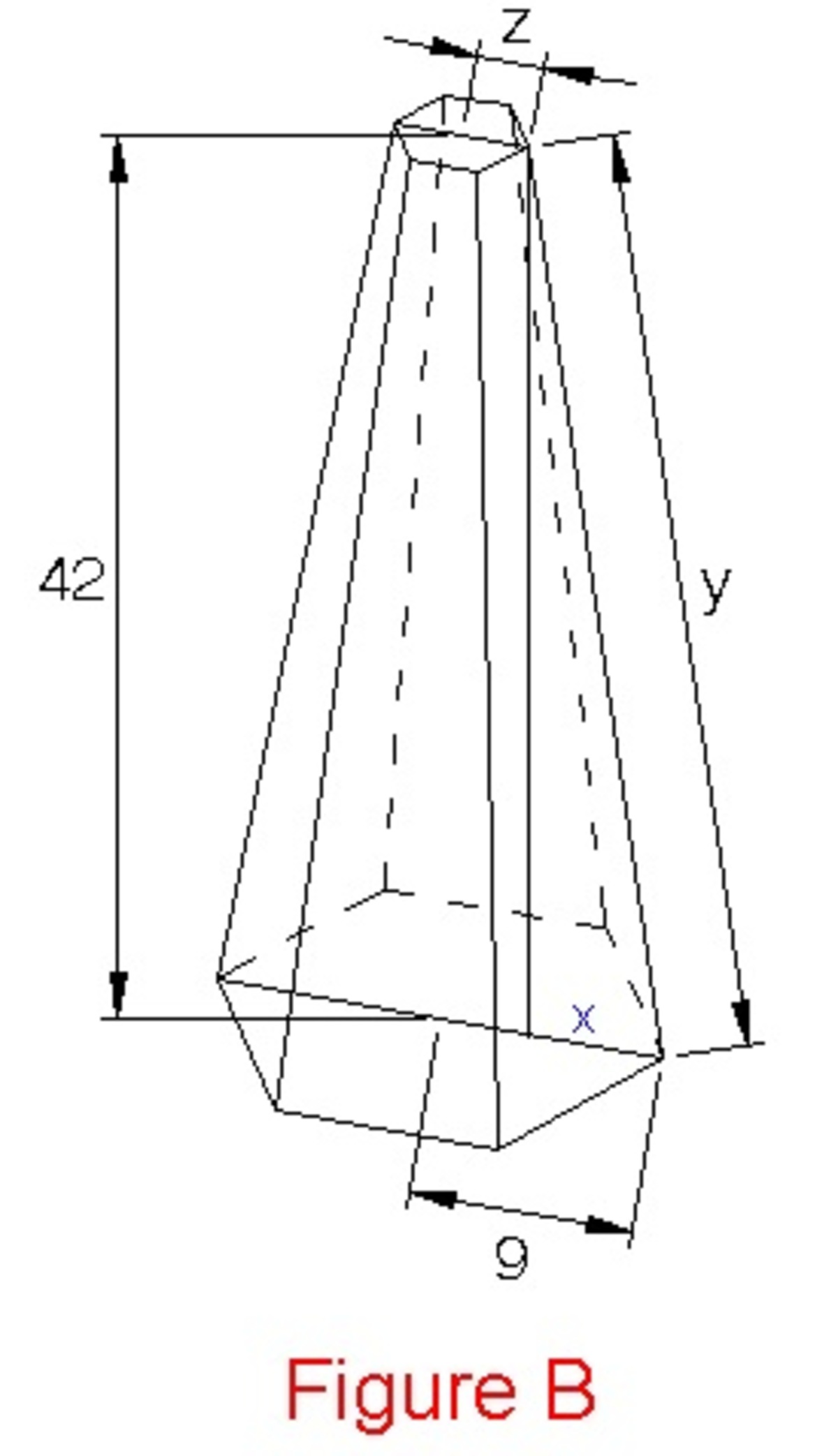
y = 4 2 2 + 6 . 3 2 = 1 8 0 3 . 6 9
z = 9 − x ⟹ z = 9 − 6 . 3 = 2 . 7
a = 2 9 − 2 . 7 = 3 . 1 5
L = ( 1 8 0 3 . 6 9 ) 2 − 3 . 1 5 2 ≈ 4 2 . 3 5 3
Since the figure is in the shape of a frustum of pyramid, the surface area is given by
S = 2 1 ( p + P ) ( L ) where p is the perimeter of the upper base, P is the perimeter of the lower base and L is the slant height
So, we have
S = 2 1 [ 6 ( 2 . 7 ) + 6 ( 9 ) ] ( 4 2 . 3 5 3 ) ≈ 1 4 8 7