Determinant in symmetrical form
If b c + q r = c a + r p = a b + p q = − 1 , then find the value of ∣ ∣ ∣ ∣ ∣ ∣ a p b q c r a b c p q r ∣ ∣ ∣ ∣ ∣ ∣
If you're looking to skyrocket your preparation for JEE-2015, then go for solving this set of questions .
The answer is 0.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
∣ ∣ ∣ ∣ ∣ ∣ a p b q c r a b c p q r ∣ ∣ ∣ ∣ ∣ ∣ = a p b r + a q c r + p b q c − p b c r − a p c q − a b q r = a b ( p r − q r ) + a c ( q r − p q ) + b c ( p q − p r ) = a b ( b c − c a ) + a c ( a b − b c ) + b c ( a c − a b ) = a b c ( ( b − a ) + ( a − c ) + ( c − b ) ) = 0
P.S. Notice that the − 1 is not necessary. It can be replaced with any number.
Best Solution :
let b=c=0
then you have from relations
p=q=r=i= root(-1)
(nothing has been told about them being real or not any way)
now put in determinant to get
|ai a i|
|bi b i |
|ci c i|
which is obviously 0 (as second column * i = 1st column)
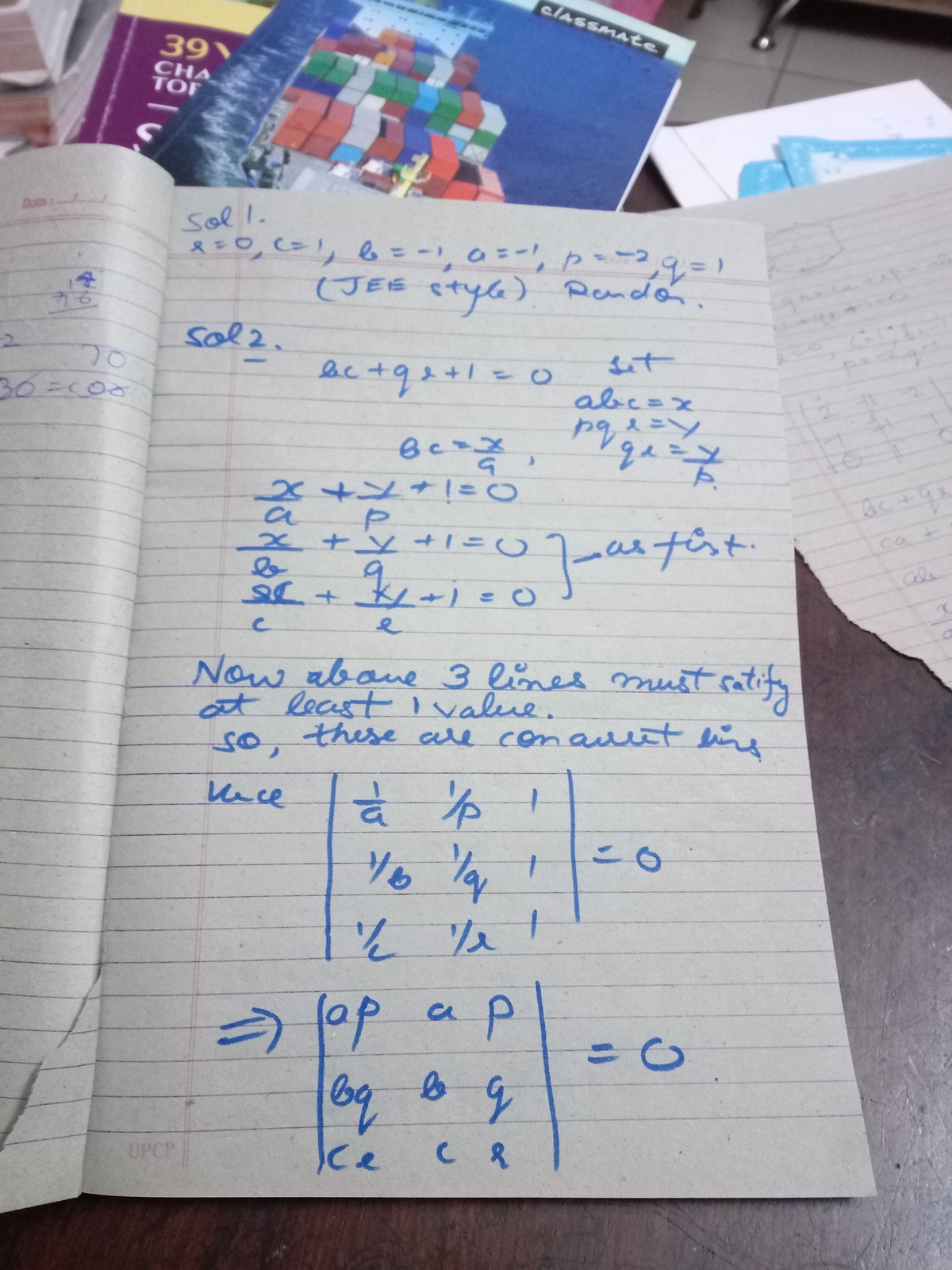
∣ ∣ ∣ ∣ ∣ ∣ a p b q c r a b c p q r ∣ ∣ ∣ ∣ ∣ ∣ = a b c p q r ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 p 1 q 1 r 1 a 1 b 1 c 1 ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 q r p r p q b c c a a b ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 q r p r p q b c + q r + 1 c a + p r + 1 a b + p q + 1 ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 q r p r p q 0 0 0 ∣ ∣ ∣ ∣ ∣ ∣ = 0