Determine the Difference
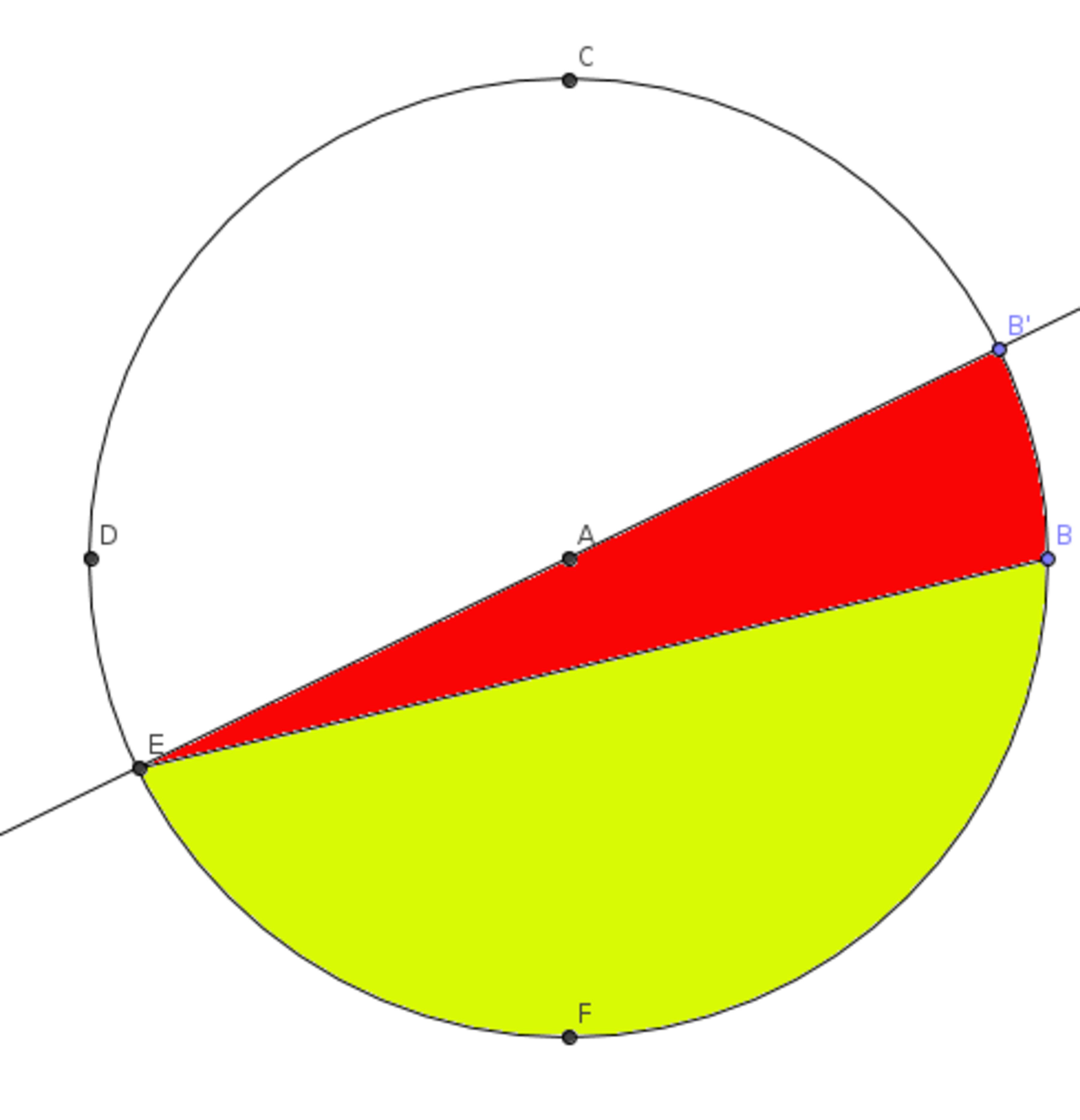
The circle above has a radius of 4 cm . If B A B ′ = 2 6 ∘ , determine the difference in areas of the yellow to the red to two decimal places. Keep in mind that E A B ′ is a straight line. (Answer is in cm 2 .)
The answer is 10.86.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
good job elvin
We can find the area of both by easily: 2 π ⋅ 1 6 ≈ 2 5 . 1 3 2 7
If B A B ′ = 2 6 ∘ , F A E = 6 4 ∘ . This means E A B = 1 5 4 ∘ . This gives us an isosceles triangle, and we can find E B by using the law of sines: E B = s i n ( 1 3 ) 4 ⋅ s i n ( 1 5 4 ) ≈ 7 . 7 9 5 0 . Now, you can use Heron's formula to find the area of the isosceles to be ≈ 3 . 5 0 7 0 . To find the rest of the red area, we simply find the area of the portion of the circle: 3 6 0 1 6 π 2 6 ≈ 3 . 6 3 0 3 . We add the two areas together to get a total red area of ≈ 7 . 1 3 7 3 . Now, the yellow area equal the half of the circle minus the red, so to find the difference between the two is simple: 2 5 . 1 3 2 7 − ( 2 ⋅ 7 . 1 3 7 3 ) ≈ 1 0 . 8 6 .
Join AB to form a sector.
Area of sector BAB' = π ∗ r 2 ∗ 3 6 0 2 6 = 3.63
Area of △ EAB = 2 1 ∗ r 2 ∗ s i n ( 1 8 0 − 2 6 ) = 3.507
Total red area = 3.63 + 3.507 = 7.137
Area of semicircle EBB' = 8 π = 25.133
Yellow area = 25.133 - 7.137 = 17.996
Yellow area - Red area = 10.86
∠ E A B = 1 8 0 − 2 6 = 1 5 4 o = 1 8 0 π 1 5 4 = 2 . 6 8 7 8 c . Y e l l o w s e g m e n t a r e a = 2 4 2 ∗ { 2 . 6 8 7 8 − S i n ( 2 . 6 8 7 8 ) } = 1 7 . 9 9 5 4 8 c m 2 . Y e l l o w + R e d a r e a = a r e a o f s e m i c i r c l e = 8 π . ∴ R e d a r e a = 8 π − 1 7 . 9 9 5 4 8 . D i f f r a n c e i n a r e a = 1 7 . 9 9 5 4 8 − ( 8 π − 1 7 . 9 9 5 4 8 ) = 2 ∗ 1 7 . 9 9 5 4 8 − 8 π = 1 0 . 8 5 9 2 c m 2 .
Interesting approach! Well done! :)
1.Connect AB to create sector
Area of sector ABB'= 26/360 pi r^2, = 3.62
Notice triangle EAB
Drop perpendicular from A to EB, call this point M
angle(B'EB)=1/2 angle(B'AB), angle(B'EB)=13
Length of AM= sin(13)=x/4, = 3.44
Combine areas of triangle AEB and sector B'AB, = 7.06
Area of Yellow area= 2 p i ∗ r 2 - 7.06 ,= 18.06
Diff of areas= 18.06-7.06, approximately 11.