Determining the area based on side lengths only?

A given set of side lengths of a quadrilateral can give different areas depending on the angles. For example, the area of a rectangle is greater than the area of a non-right parallelogram with the same sides:

Therefore, even if we know all the side lengths of a quadrilateral, we cannot determine the area of the quadrilateral.

Relevant wiki: Quadrilateral Classification

First, since there is no quadrilateral version of Heron's formula, I conjectured that the correct answer is no. In order to prove this, we can use the fact that there are two types of quadrilaterals: concave and convex.

First, let us begin with a convex kite $ABCD$ :

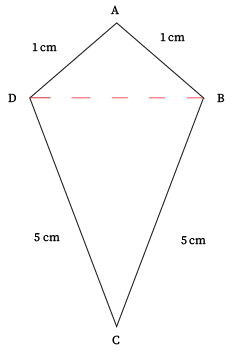
Draw a red dotted line along $BD$ ; this will be helpful in a moment. Now, reflect $\triangle ABD$ over $BD$ :

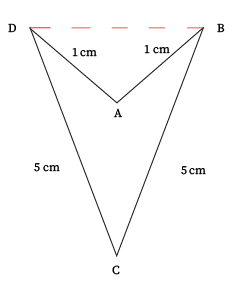
Notice that we still have the same side lengths as before, just in a different position. Note that this new concave quadrilateral has a different area:

$A'_{ABCD}=A_{ABCD}-2A_{\triangle ABD}$

Therefore, my conjecture is correct; the correct answer is no .

This isnot how I solve the problem however, I wish to post this as my alternative solution.

Bretschneinder's generalizes the Brahmagupta's formula for the area of cyclic qaudrilateral and which in turn generalized the Hero's formula for area of triangle which is as follow. $K^2= (s-w)(s-x)(s-y)(s-z) - wxyz\cos ^2\left(\frac{\text{sum of opp. angles of quad}}{2}\right)$ To calculate the area we are in need to opposite angles of qaudrilateral which implies we cannot find the area.

Note: In case of maximum area the answer is yes .

If you calculate the area of a square and a regular lozenge with a side length 1 then the area of the square : a^2 = 1 and the area of the lozenge : sin(π\3)= $\frac { \sqrt { 3 } }{ 2 }$

Atleast one angle is needed additionally to determine the area of a quadrilateral with known sides.

The length of the diagonal will be used in Heron's formulae. The problem is despite the two triangles formed due to a diagonal we will not be able to get rid of the diagonal value.

Second issue is that due to concave or convex nature of quadrilateral it is very difficult as for concave the diagonal could be outside the closed figure and calculation of area will be wrong. With these two points I concluded that the ans is no.

If a = c and b= d. A quadrilateral could be constructed in which the opposite angles approach 0 and the area will also approach 0. The same side lengths could produce an area of a x b. This it is not possible to calculate the area.

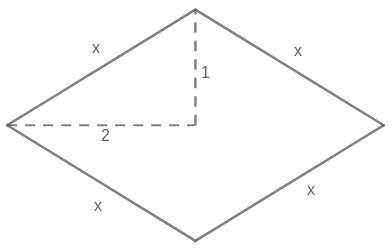
The diamond above must have area 4 by symmetry, but Pythagoras' theorem gives $x^2 = 2^2 + 1^2 = 5$ . So the square with the same side length has a different area.

Dislike this phrasing. There is nothing about knowing the four side lengths of a quadrilateral that would prevent one from being able to compute the area, should more information also be known. Now it's certainly true that the four side lengths in isolation would not be sufficient to calculate the area of a quadrilateral. Indeed, the side lengths of a rhombus would not be sufficient. Given any side length $s$ we can find a rhombus of any area $A$ satisfying $0 < A \leq s^2$ .

By dividing the quadilateral into two triangles....

The area may be calculated if the vertices of the quadrilateral lie on the circumference of a circle by Brahmagupta's formula, which is a generalization of Herron's formula; to wit: A= sqrt(s(s - a)(s _ b)(s - c)), where s = (p/2)(a + b + c). Ed Gray